WinHex18.4算法分析

经过分析,注册码分为六个部分:

Name: "xxx"

Addr1: "yyy"

Addr2: "zzz" 这三个字符不代表长度

Key1: "32个十六进制数的字符串" 它在内存中的形式是:比如字符串是

"18A519949D4E5F1FAED08A3EAB7CC665" 它会以两个字符为单位作为一个字节, 以顺序列在内存中  ===> 18 A5 19 94 等等

Key2: "32个十六进制数字符串" 同上

Chksm: "kk" 就一个字节

以上的六个部分的后半个部分会被拷贝到以下位置:

xxx 5e2f14

yyy 5e2f65

zzz 5e2fa2

key1的值 5e2fdf

key2的值 5e2fef

key1和key2中的值在内存中是紧密相连的.

Chksm的值 5e30f9

以上六个部分的前半个部分,会进行比较, 也就是说必须一模一样. 除了中间的空格还可以被替换成其他字符

用PEID查看发现未加壳,之后查看导入表,发现关键函数

在lstrcmpiA下断,随意输入注册码,之后发现,注册判断函数在sub_568A74

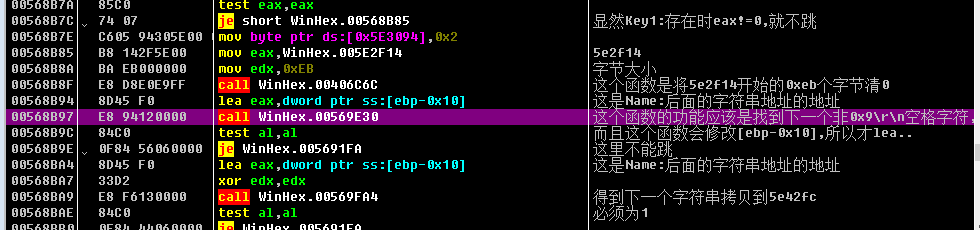
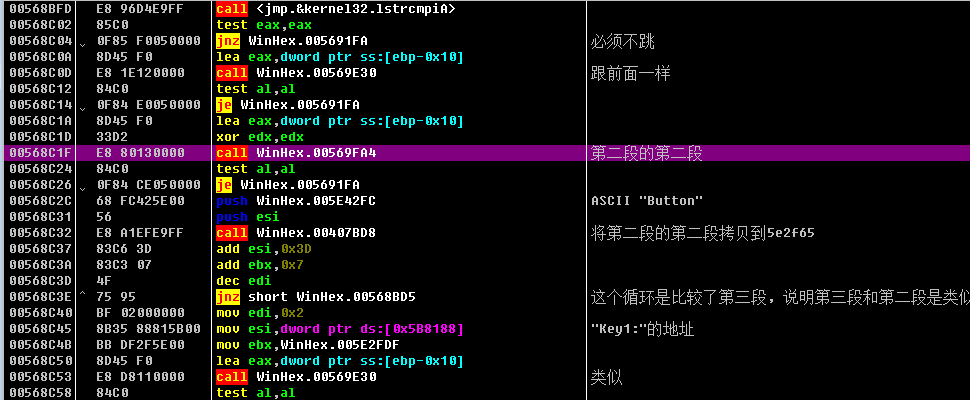
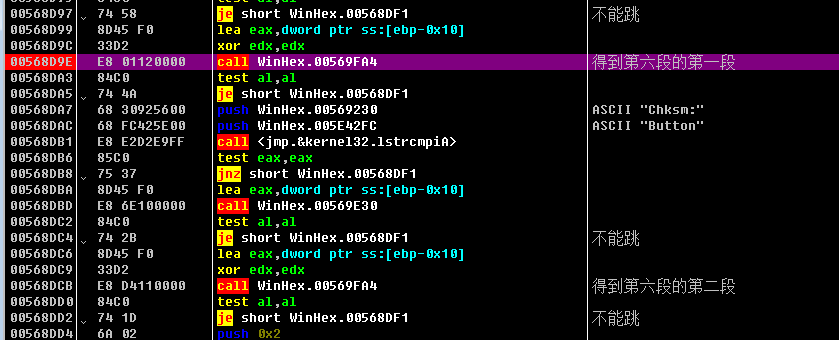
整串字符串的分离和拷贝跟sub_569fa4有关, 他会清除一些分隔符, 进入下一部分.

六个部分的前半部分都是以如下的形式进行检测的:

其中5e42fc是一个中转站:

在sub_569fa4中,会将分离出来的字符串拷贝到5e42fc中,如果是后半部分的字符串那么还会拷贝到[5e2F14,+0xeb)的相应位置

以上是六段注册码的分离以及部分检测.

下面是checksum的值的计算方式:

就是把5e2f14开始的0xeb个字节, 以字节为单位全部相加

由于这个数据块前面已经置过0, 所以不会有其他影响因素.

checksum就是把5个部分的后半部分以字节为单位全部相加,得到的值的低字节,就是checksum的值了.

另外0x5e3238的值决定了软件的到期时间

0x5e3238的值是由key1的首word和尾word异或得到的, 得注意字节序, 这个值必须在[46e4,5221)之间,高字节必须&&0x80==0

key1的倒数第3个字节 byte_5e2fec and 0x1f == 0x13 ==>5e2fec == 0x13 或0x33 0x53 73 93 b3 e3

byte_5e2fec/32 ==> 5e31a2 !=5,8,6 那么b3就不行了` 0 1 2 3 4 5 6

byte_5e31a2 [2,6]

Name: "aaaa"
Addr1: "bbbb"
Addr2: "cccc"
Key1: "2A3C1111111111111111111111535770"
Key2: "11111111111111111111111111111111"
Chksm: "E3"

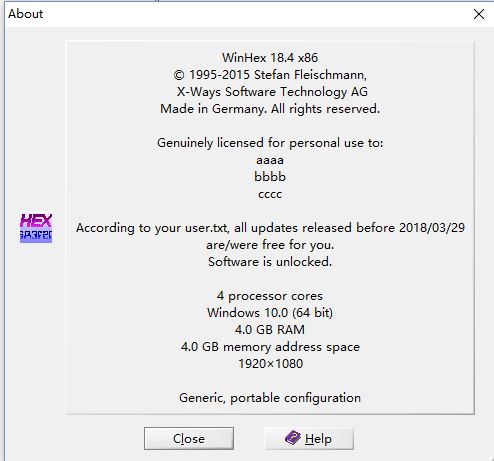
Genuinely Licensed for personal use. 个人使用

Software is unlocked. All Updates released before 2018/03/28 are free for me.

软件已经解锁. 2018年3月28日以前的所有升级对我来说都是免费的.