[LeetCode] Mirror Reflection 镜面反射

There is a special square room with mirrors on each of the four walls.  Except for the southwest corner, there are receptors on each of the remaining corners, numbered `0`, `1`, and `2`.

The square room has walls of length p, and a laser ray from the southwest corner first meets the east wall at a distance q from the 0th receptor.

Return the number of the receptor that the ray meets first.  (It is guaranteed that the ray will meet a receptor eventually.)

Example 1:

Input: p = 2, q = 1
Output: 2
Explanation: The ray meets receptor 2 the first time it gets reflected back to the left wall.

Note:

1. 1 <= p <= 1000
2. 0 <= q <= p

这道题给了我们一个正方形的房间，说是四面都是镜子墙，然后在西南角有一个激光发射器，其余三个角都有接收装置，问我们最终激光会被哪个接收器接收。第一次读题时这句 "Return the number of the receptor that the ray meets first." 让博主理解错误了，以为是让返回接收器的个数，以为接收器也能反射激光到其对角的接收器，那么接收器2和0互相反射，就是返回经过了2个接收器，接收器1返回到反射点，就是返回经过了1个接收点，想的是一套一套的，结果人家让返回的是接收器的标号，个人觉得将 number 改为 index 会减少些歧义。无所谓了，反正最终搞懂了题意就行了。其实这道题的正确解法还挺难想的，因为大家很容易走进的误区就是研究反射角啥的，然后算具体反射到了哪一个位置，再算下一个位置，其实这样都将题目变复杂了。博主把这一类型归为脑筋急转弯 Brain Teaser，一般都有很巧妙的数学解法，并不需要太复杂的算法。

首先从最简单的情况开始分析，当p和q相等的时候，那么激光直接到达接收器1，当 p/q = 2 的时候，就如例子中所示，经过右边的镜面反射后到达左上角的接受器2。那么我们再来考虑下这三种情况 p/q = 3, p/q = 4, p/q = 3/2，并画出折射情况如下所示：

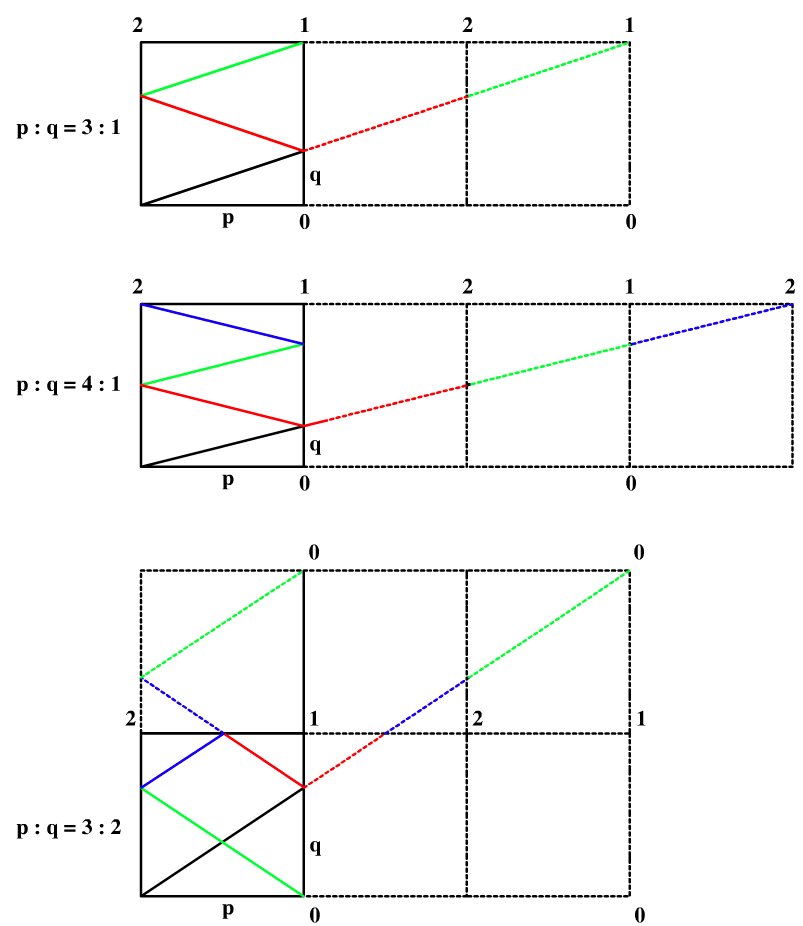
这里就有些比较好玩的规律了，我们知道激光遇到镜面是会发生折射的，但是假如没有镜面，就会仍然沿直线前进，那么对于 p/q = 3 时，若我们在右边增加大小相同的2个房间，则激光会到达右上角，由于第二个房间和原始房间是镜面对称的，而第三个房间和第二个房间也是镜面对称的，则第三个房间和原始房间就是一样的了，那么就可以假设一下，奇数房间和原始房间的布局相同。再来看上图中的 p/q = 4 时，我们在右边复制了三个房间，在第四个房间的时候，激光到达了右上角，而第偶数个房间的布局是跟原始房间称镜面反射的，则就是接受器2了。其实有些时候，我们不止要在右边复制房间，还需要在上面复制房间，比如当 p/q = 3/2 时，我们需要复制出一个 2x3 大小的矩阵出来，在水平方向共有三个房间，是奇数则水平方向和原始房间布局一致，但是竖直方向也复制了房间，那么竖直方向有偶数个房间，则竖直方向和原始房间成镜面反射，则最右上角为接收器0。

分析到这里，我们应该已经能总结出规律如下了：

• p为奇数，q为奇数时，到达接收器1。
• p为奇数，q为偶数时，到达接收器0。
• p为偶数，q为奇数时，到达接收器2。

那你可能会有疑问了，为啥没有p和q均为偶数的情况呢？比如 p = 4, q = 2，其实只要我们画个图就知道，这个跟 p = 2, q = 1 的情况是一摸一样的，若p和q均为偶数，那么那么一定可以同时除以2，那么其实我们可以先对p和q进行判断，若二者同为偶数，则同时除以2，直到不同时为偶数时，然后再带入上面归纳的三种情况求解即可，参见代码如下：

解法一：

class Solution {
public:
    int mirrorReflection(int p, int q) {
        while (p % 2 == 0 && q % 2 == 0) {
            p /= 2; q /= 2;
        }
        if (p % 2 == 0) return 2;
        if (q % 2 == 0) return 0;
        return 1;
    }
};

其实我们可以进一步化简，将三种情况融为一个表达式即可，即 1 - p%2 + q%2，不信的话可以带数字验证一下，碉堡了有木有，参见代码如下：


解法二：

class Solution {
public:
    int mirrorReflection(int p, int q) {
        while (p % 2 == 0 && q % 2 == 0) {
            p /= 2; q /= 2;
        }
        return 1 - p % 2 + q % 2;
    }
};

其实不光是p和q同时为偶数的时候可以化简，只要p和q的最大公约数 Greatest Common Divisor 大于1时，都可以化简，比如，若 p = 6, q = 3 时跟 p = 2, q = 1 的情况也是一样，那我们就可以先求出p和q的最大公约数，然后用p和q分别除以这个最大公约数，再带入上面的那个一行公式求解即可，参见代码如下：


解法三：

class Solution {
public:
    int mirrorReflection(int p, int q) {
        return 1 - p / gcd(p, q) % 2 + q / gcd(p, q) % 2;
    }
    int gcd(int p, int q) {
    	return q ? gcd(q, p % q) : p;
    }
};

Github 同步地址:

https://github.com/grandyang/leetcode/issues/858

参考资料：

https://leetcode.com/problems/mirror-reflection/

https://leetcode.com/problems/mirror-reflection/discuss/141765/Java-short-solution-with-a-sample-drawing

https://leetcode.com/problems/mirror-reflection/discuss/141826/1-line-C%2B%2B-solution-using-gcd-only-4ms

https://leetcode.com/problems/mirror-reflection/discuss/141773/C%2B%2BJavaPython-1-line-without-using-any-package-or

[LeetCode All in One 题目讲解汇总(持续更新中...)](https://www.cnblogs.com/grandyang/p/4606334.html)