java项目---用java实现二叉平衡树（AVL树）并打印结果（详）(3星)

 package Demo;

 public class AVLtree  {
     private Node root;                      //首先定义根节点

     private static class Node{                              //定义Node指针参数
         private int key;                //节点
         private int balance;                    //平衡值
         private int height;             //树的高度
         private Node left;                      //左节点
         private Node right;             //右节点
         private Node parent;                    //父母节点

     Node(int key, Node parent){             //构造器中引用该构造器正在初始化的对象
         this.key = key;
         this.parent = parent;

         }
     }
     public boolean insert(int key){             //判断这里是否能插入新的节点
         if(root == null){
             root = new Node(key,null);
             return true;
         }

         Node n = root;
         while (true){                           //如果根节点下的子节点和新插进来的子节点相同
             if(n.key == key)
                 return false;                   //则不进行插入操作

             Node parent = n;

             boolean goLeft = n.key > key;           //判断新的节点插入父母节点的左边or右边
             n = goLeft ? n.left : n.right;             //小的话插左边，大的话插右边

             if(n == null){
                 if(goLeft){
                     parent.left = new Node (key,parent);
                 }else{
                     parent.right = new Node(key,parent);
                 }
                 rebalance(parent);
                 break;
             }
         }
         return true;
     }

     private void delete(Node node){                     //删除节点
         if(node.left == null && node.right == null){
             if(node.parent == null){
                 root = null;
             }else{
                 Node parent = node.parent;
                 if(parent.left == node){            //如果父母节点的左孩子节点和根节点一样
                     parent.left = null;             //则左节点为空
                 }else{
                     parent.right = null;            //反之右节点为空
                 }
                 rebalance(parent);
             }
             return ;
         }

         if(node.left != null){              //如果左节点不空
             Node child = node.left;
             while(child.right != null)child = child.right;
             node.key = child.key;
             delete(child);
         }else{
             Node child = node.right;
             while (child.left != null)child = child.left;
             node.key = child.key;
             delete(child);
             }
         }

         public void Delete(int delKey){
         if(root == null)
             return;

         Node child = root;
         while (child != null){
             Node node = child;                           //交换根节点给node , 再判断新的孩子节点插在哪里
             child = delKey >= node.key ? node.right : node.left;
             if(delKey == node.key){
                 delete(node);
                 return;
             }
         }
     }

     private void setBalance(Node... nodes){
         for(Node n : nodes){
             reheight(n);
             n.balance = height(n.right) - height(n.left);           //平衡因子，任意节点左右子树高度差
         }
     }

     private void rebalance (Node n){
         setBalance(n);

         if(n.balance == -2){
             if(height(n.left.left) >= height(n.left.right))
                 n = rotateRight(n);
             else
                 n = rotateLeftThenRight(n) ;

         }else if(n.balance == 2){                                   //等于2和-2都是不平衡的，需要重新调整
             if(height(n.right.right) >= height(n.right.left))
                 n = rotateLeft(n);
             else
                 n = rotateRightThenLeft(n);

         }

         if(n.parent != null){
             rebalance(n.parent);
         }else{
             root = n;
         }
     }

     private Node rotateLeft(Node a){

         Node b = a.right;
         b.parent = a.parent;

         a.right = b.left;

         if(a.right != null)
             a.right.parent = a;

         b.left = a;
         a.parent = b;

         if(b.parent != null){
             if(b.parent.right == a){
                 b.parent.right = b;
             }else{
                 b.parent.left = b;
             }
         }

         setBalance(a, b);

         return b;
     }

     private Node rotateRight(Node a){

         Node b = a.left;
         b.parent = a.parent;

         a.left = b.right;

         if(a.left != null){
             a.left.parent = a;

             b.right = a;
             a.parent = b;

             if(b.parent.right == a){
                 b.parent.right = b;
             }else{
                 b.parent.left = b;
             }
         }

         setBalance(a, b);

         return b;
     }

     private Node rotateLeftThenRight(Node n){
         n.left = rotateLeft(n.left);
         return rotateRight(n);
     }

     private Node rotateRightThenLeft(Node n){
         n.right = rotateRight(n.right);
         return rotateLeft(n);
     }

     private int height (Node n){
         if(n == null)
             return -1;
         return n.height;
     }

     public void printBalance(){
         printBalance(root);
     }

     private void printBalance(Node n){
         if(n != null){
             printBalance(n.left);
             System.out.printf("%s ",n.balance);
             printBalance(n.right);
         }
     }

     private void reheight(Node node){
         if(node != null){
             node.height = 1 + Math.max(height(node.left),height(node.right));           //新的二叉平衡树高度为：
         }
     }
     public static void main(String[] args) {
         AVLtree tree = new AVLtree();

         System.out.println("Inserting values 1 to 10");     //最后输出的结果代表平衡因子，0为左右子树高度相等，1为左右子树高度相差1层
         for (int i = 1; i < 10; i++)
             tree.insert(i);

         System.out.println("Print balance : ");
         tree.printBalance();
     }
 }

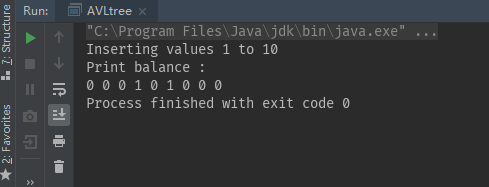　　　　可以动手画一下生成的AVL树，亲测算法符合结果。