[NOIP 2015TG D2T3] 运输计划

题目背景

公元 2044 年,人类进入了宇宙纪元。

题目描述

L 国有 n 个星球,还有 n-1 条双向航道,每条航道建立在两个星球之间,这 n-1 条航道连通了 L 国的所有星球。

小 P 掌管一家物流公司,该公司有很多个运输计划,每个运输计划形如:有一艘物

流飞船需要从 ui 号星球沿最快的宇航路径飞行到 vi 号星球去。显然,飞船驶过一条航道是需要时间的,对于航道 j,任意飞船驶过它所花费的时间为 tj,并且任意两艘飞船之间不会产生任何干扰。

为了鼓励科技创新,L 国国王同意小 P 的物流公司参与 L 国的航道建设,即允许小 P 把某一条航道改造成虫洞,飞船驶过虫洞不消耗时间。

在虫洞的建设完成前小 P 的物流公司就预接了 m 个运输计划。在虫洞建设完成后, 这 m 个运输计划会同时开始,所有飞船一起出发。当这 m 个运输计划都完成时,小 P 的物流公司的阶段性工作就完成了。

如果小 P 可以自由选择将哪一条航道改造成虫洞,试求出小 P 的物流公司完成阶段性工作所需要的最短时间是多少?

输入输出格式

输入格式：

输入文件名为 transport.in。

第一行包括两个正整数 n、m,表示 L 国中星球的数量及小 P 公司预接的运输计划的数量,星球从 1 到 n 编号。

接下来 n-1 行描述航道的建设情况,其中第 i 行包含三个整数 ai, bi 和 ti,表示第

i 条双向航道修建在 ai 与 bi 两个星球之间,任意飞船驶过它所花费的时间为 ti。

接下来 m 行描述运输计划的情况,其中第 j 行包含两个正整数 uj 和 vj,表示第 j个运输计划是从 uj 号星球飞往 vj 号星球。

输出格式：

输出共1行,包含1个整数,表示小P的物流公司完成阶段性工作所需要的最短时间。

输入输出样例

输入样例#1：

输出样例#1：

说明

所有测试数据的范围和特点如下表所示

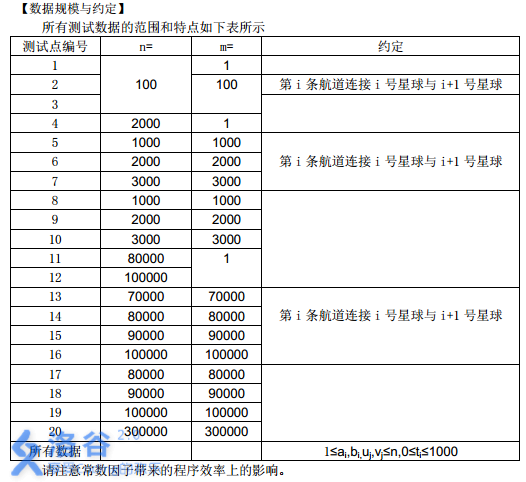
请注意常数因子带来的程序效率上的影响。

好烦呐。。。

让我们一步一步对这道难题深入分析。

1.整棵树在整个过程中改变的只有1条边的权值，其他边与树的结构都没变化，这是很重要的；

2.我们要在很短的时间内要知道这棵树中任意两点间的距离——那么我们就要选择比较优秀的算法了。由于n，m很大，所以我们能选的较为不错的，一个是用LCA来解，另一个就是用树链剖分（我个人认为树链剖分写起来更快，而且更容易查错）；

3.我们必定要将m条路径中，起点终点的LCA求出，作为中转站，便于解题；

4.仔细读题目，任务是让我们求最小的最大值，那么我们自然而然会想到二分；

5.假设我们用树链剖分先将m条路线两点距离等需要的量预处理出来，需要mlogn的时间，而二分又是log级别的，所以主要考虑的还要放在二分的check上面；

6.check怎么来？不慌，按照题目中要求的。当然，不能枚举每条边再判断，否则这样的复杂度已经到了nlog(R-L)，意味着判断的过程要在log级别以下，这是完全不可能的（你还要枚举路径呢（m条））。那怎么办？对于这题，check成功的条件更容易判断。怎样算check成功？假设，当前二分的最大值为high，如果m条路径中dis大于high的都记录下来（可以之前就排趟序），假设有cnt条，然后，我们要找一条边，将这条边权值变为0后，要达到m条路径的dis都小于等于high的目的，说明这cnt条“超标”路径必定经过这条边，并且dis[当前路径]-w[当前边]<=high，这样才行；

7.那怎么记录每条边被经过的次数？首先，我们会有一个暴力的想法（真的暴力），如果一条路径(x,y)“超标”，那么将x-->LCA(x,y)和y-->LCA(x,y)经过的边都加上1个经过次数。但是这样实在太慢（只有80分，算不错了），毕竟如果出现链状，时间就退化成线性的了（而且这个链也非可以剖分的树链）。那么怎么优化？我们想到了差分的方法（我真心没想到）。像上面这个例子，就把f[x]++，f[y]++，f[LCA(x,y)]-=2，其中f[i]表示的是从节点i到其父节点的次数（1当然没有），我们可以用DFS累加的方式求出所有边经过的次数。这样，check这个过程的复杂度就降到了O(n)左右，不虚了；

8.当然这种题目肯定都要卡常的，在评测时我加了一句话，出现了神奇的一幕。。。我先用第一种方法（步骤7里），在check开头加了一句if (a[1].dis>high+1000) return 0;（其中a数组按关键字dis从大到小排序），结果就A了！在第二种方法写上同样的东西，跑得反而没有第一种快，还TLE了1个点。。。[yun]蒽哼哼，我想，这也许就是“神剪枝”的威力吧。。。orz ○|￣|_

下面给出两份代码：

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<queue>
 #define Me(Arr) memset(Arr,0,sizeof Arr);
 using namespace std;
 ,maxe=;
 int n,m,L,R,mid,ans;
 int lnk[maxn],nxt[maxe],son[maxe],w[maxe],id[maxe],wsin[maxn],pointto[maxn],tot;
 int size[maxn],fa[maxn],dep[maxn],gonxt[maxn],top[maxn];
 int bel[maxn],wei[maxn],wtofa[maxn],cnt;
 int f[maxn];
 struct data{
     int x,y,dis,LCA;
     bool operator < (const data &u) const {return dis>u.dis;}
 }a[maxn];
 int read(){
     ; char ch=getchar();
     ') ch=getchar();
     +ch-',ch=getchar();
     return x;
 }
 void INIT(){
     tot=cnt=;
     Me(lnk); Me(nxt); Me(son); Me(w); Me(id); Me(wsin); Me(wtofa); Me(pointto);
     Me(size); Me(fa); Me(dep); Me(gonxt); Me(top); Me(wei); Me(bel);
     top[]=cnt=bel[]=,L=,R=-;
 }
 void add(int i,int x,int y,int z){
     nxt[++tot]=lnk[x],son[tot]=y,w[tot]=z,id[tot]=i,lnk[x]=tot;
 }
 void DFS_1(int x,int u,int layer){
     size[x]=,fa[x]=u,dep[x]=layer;
     for (int j=lnk[x]; j; j=nxt[j]) if (son[j]!=u){
         DFS_1(son[j],x,layer+); size[x]+=size[son[j]],wtofa[son[j]]=w[j],pointto[son[j]]=id[j];
         if (size[gonxt[x]]<size[son[j]]) gonxt[x]=son[j],wei[x]=w[j];
     }
 }
 void DFS_2(int x){
     if (gonxt[x]) top[gonxt[x]]=top[x],bel[gonxt[x]]=bel[x],DFS_2(gonxt[x]),wei[x]+=wei[gonxt[x]];
     for (int j=lnk[x]; j; j=nxt[j]) if (son[j]!=fa[x]&&son[j]!=gonxt[x]) top[son[j]]=son[j],bel[son[j]]=++cnt,DFS_2(son[j]);
 }
 void prepare(){
     DFS_1(,,); DFS_2();
 }
 ?x:-x;}
 int get(int i,int x,int y){
     ;
     while (bel[x]!=bel[y])
         if (dep[top[x]]>dep[top[y]]) ret+=wei[top[x]]-wei[x]+wtofa[top[x]],x=fa[top[x]];
         else ret+=wei[top[y]]-wei[y]+wtofa[top[y]],y=fa[top[y]];
     ret+=abso(wei[x]-wei[y]);
     a[i].LCA=dep[x]<dep[y]?x:y;
     return ret;
 }
 void work(int u,int v,int LCA){
     while (u!=LCA) f[pointto[u]]++,u=fa[u];
     while (v!=LCA) f[pointto[v]]++,v=fa[v];
 }
 bool jug(int high){
     ].dis>high+) ;
     Me(f); ].dis-high,cnt=;
     ; i<=m; i++) if (a[i].dis>high) work(a[i].x,a[i].y,a[i].LCA),cnt++; else break;
     ;
     ; i<n; i++) ;
     ;
 }
 int main(){
     n=read(),m=read(),INIT();
     ; i<n; i++){
         int x=read(),y=read(),z=read(); add(i,x,y,z),add(i,y,x,z); wsin[i]=z;
     }
     prepare();
     ; i<=m; i++) a[i].x=read(),a[i].y=read(),a[i].dis=get(i,a[i].x,a[i].y),R=max(R,a[i].dis);
     sort(a+,a++m);
     while (L<=R){
         mid=(L+R)>>;
         ; ;
     }
     printf("%d",ans);
     ;
 }

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<queue>
 #define Me(Arr) memset(Arr,0,sizeof Arr);
 using namespace std;
 ,maxe=;
 int n,m,L,R,mid,ans;
 int lnk[maxn],nxt[maxe],son[maxe],w[maxe],tot;
 int size[maxn],fa[maxn],dep[maxn],gonxt[maxn],top[maxn];
 int bel[maxn],wei[maxn],wtofa[maxn],cnt;
 int f[maxn];
 struct data{
     int x,y,dis,LCA;
     bool operator < (const data &u) const {return dis>u.dis;}
 }a[maxn];
 int read(){
     ; char ch=getchar();
     ') ch=getchar();
     +ch-',ch=getchar();
     return x;
 }
 void INIT(){
     tot=cnt=;
     Me(lnk); Me(nxt); Me(son); Me(w); Me(wtofa);
     Me(size); Me(fa); Me(dep); Me(gonxt); Me(top); Me(wei); Me(bel);
     top[]=cnt=bel[]=,L=,R=-;
 }
 void add(int i,int x,int y,int z){
     nxt[++tot]=lnk[x],son[tot]=y,w[tot]=z,lnk[x]=tot;
 }
 void DFS_1(int x,int u,int layer){
     size[x]=,fa[x]=u,dep[x]=layer;
     for (int j=lnk[x]; j; j=nxt[j]) if (son[j]!=u){
         DFS_1(son[j],x,layer+); size[x]+=size[son[j]],wtofa[son[j]]=w[j];
         if (size[gonxt[x]]<size[son[j]]) gonxt[x]=son[j],wei[x]=w[j];
     }
 }
 void DFS_2(int x){
     if (gonxt[x]) top[gonxt[x]]=top[x],bel[gonxt[x]]=bel[x],DFS_2(gonxt[x]),wei[x]+=wei[gonxt[x]];
     for (int j=lnk[x]; j; j=nxt[j]) if (son[j]!=fa[x]&&son[j]!=gonxt[x]) top[son[j]]=son[j],bel[son[j]]=++cnt,DFS_2(son[j]);
 }
 void DFS_3(int x){
     for (int j=lnk[x]; j; j=nxt[j]) if (son[j]!=fa[x]) DFS_3(son[j]),f[x]+=f[son[j]];
 }
 void prepare(){
     DFS_1(,,); DFS_2();
 }
 ?x:-x;}
 int get(int i,int x,int y){
     ;
     while (bel[x]!=bel[y]){
         if (dep[top[x]]>dep[top[y]]) ret+=wei[top[x]]-wei[x]+wtofa[top[x]],x=fa[top[x]];
         else ret+=wei[top[y]]-wei[y]+wtofa[top[y]],y=fa[top[y]];
     }
     a[i].LCA=dep[x]<dep[y]?x:y;
     ret+=abso(wei[x]-wei[y]);
     return ret;
 }
 bool jug(int high){
     ].dis>high+) ;
     ].dis<=high) ;
     Me(f); ].dis-high,cnt=;
     ; i<=m; i++) ,cnt++; else break;
     DFS_3();
     ; i<=n; i++) ;
     ;
 }
 int main(){
     n=read(),m=read(),INIT();
     ; i<n; i++){
         int x=read(),y=read(),z=read(); add(i,x,y,z),add(i,y,x,z);
     }
     prepare();
     ; i<=m; i++) a[i].x=read(),a[i].y=read(),a[i].dis=get(i,a[i].x,a[i].y),R=max(R,a[i].dis);
     sort(a+,a++m);
     while (L<=R){
         mid=(L+R)>>;
         ; ;
     }
     printf("%d",ans);
     ;
 }