方差variance, 协方差covariance, 协方差矩阵covariance matrix | scatter matrix | weighted covariance | Eigenvalues and eigenvectors

covariance, co本能的想到双变量，用于描述两个变量之间的关系。

correlation，相关性，covariance标准化后就是correlation。

covariance的定义：

期望，实例减去均值，积

covariance matrix也就是相关性矩阵的原始形式，描述了一群变量之间的相互关系

一下是一个例子：

For eg here’s an example :

Covariance matrix is of dimension #cols * #cols, diagonal represents the variance of each variable (obviously as it gets calculated with itself)

From figure you can see that, English and Art have no relationship, while Math and English tends to covary very positively.

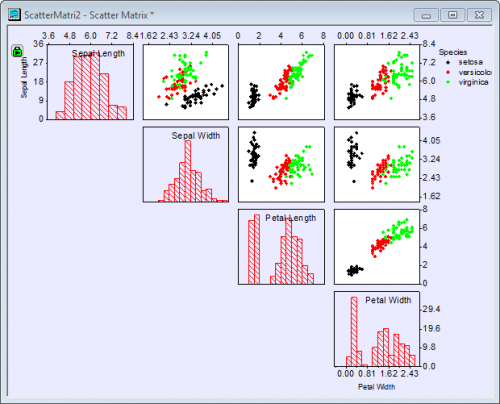
A scatter matrix consists of several pair-wise scatter plots of variables presented in a matrix format. It can be used to determine whether the variables are correlated and whether the correlation is positive or negative. This tutorial will show you how to create a Scatter Matrix plot.

weighted covariance

Eigenvalues and eigenvectors

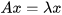
把式子中的看作一个线性变换，那么这个定义式就表示对于 向量而言，经过变换之后该向量的方向没有变化（可能会反向），而只是长度变化了（乘以 ）。也就是对于变换来说，存在一些“不变”的量（比如特征向量的方向），我想，“特征”的含义就是“不变”。而特征值，如你所见，就是变换  在特征方向上的伸展系数吧。

知乎

参考：

如何通俗易懂地解释「协方差」与「相关系数」的概念？（非常通俗易懂）

浅谈协方差矩阵

方差（variance）

集合中各个数据与平均数之差的平方的平均数。在概率论与数理统计中，方差（Variance）用来度量随机变量和其数学期望（即均值）之间的偏离程度。  方差越大，数据的离散程度就越大。

协方差（covariance）

协方差表示的是两个变量总体误差的方差，这与只表示一个变量误差的方差不同。如果两个变量的变化趋势一致，也就是说如果其中一个大于自身的期望值，另外一个也大于自身的期望值，那么两个变量之间的协方差就是正值。  如果两个变量的变化趋势相反，即其中一个大于自身的期望值，另外一个却小于自身的期望值，那么两个变量之间的协方差就是负值。如果X与Y是统计独立的，那么二者之间的协方差就是0，反之则不成立。
表达式：期望值分别为E(X) = μ 与 E(Y) = ν 的两个实数随机变量X与Y之间的协方差定义为：COV(X，Y)=E[(X-E(X))(Y-E(Y))]

协方差矩阵 （covariance matrix）

标准差和方差一般是描述一维数据的，描述多维数据就要用到协方差，协方差多了放在一起就是协方差矩阵。协方差矩阵是一个矩阵，其每个元素是各个向量元素之间的协方差。是从标量随机变量（也就是单维或单值随机变量）到高维度随机向量的自然推广。

总结

理解协方差矩阵的关键就在于牢记它的计算是不同维度之间的协方差，而不是不同样本之间。拿到一个样本矩阵，最先要明确的就是一行是一个样本还是一个维度，心中明确整个计算过程就会顺流而下，这么一来就不会迷茫了。