Linux系统添加应用服务进程的守护进程

　　以前曾在Linux上维护应用服务，但是只是简单的迭代版本等工作，没有什么技术含量。最近部署在Linux服务器上的一个平台的总线进程broker（下面总线用broker指代）经常挂掉，由于总线负责服务之间通讯，分发消息给各个应用服务，总线一旦挂掉就导致整个平台瘫痪。总线进程挂掉需要人工重启，在没有找到具体原因前维护起来很不方便，而且往往是用户先发现才反馈过来，所以先写一个守护进程，一旦总线挂掉就重启。网上查了很多资料，总算搞出来了，大体写一下实现步骤，即是备忘也分享给大家，相互交流。

　　先说一下大体思路：

　　1、创建一个脚本文件middle_start，循环查找broker进程是否存在，如果不存在就启动broker；

　　2、另外创建一个启动脚本start，启动middle_start，指定middle_start为后台进程；

　　3、再创建一个结束end，先结束守护进程，再结束broker。

　　第一步的middle_start代码如下：

#! /bin/bash
sysctl -w net.core.wmem_default=
sysctl -w net.core.wmem_max=
sysctl -w net.core.rmem_default=
sysctl -w net.core.rmem_max=
#program directory path
PRO_PATH=$PWD
#program name
PRO_NAME="/broker"
#program path, not need configure.
PRO_MAIN=$PRO_PATH$PRO_NAME
#GNOME start program， not need configure.
PROGRAM_GNOME="gnome-terminal -e \"$PRO_MAIN\""
#start    method GNOME or nohup (eg: GNONE-->STAR_PRO=$PROGRAM_GNOME ; nohup-->STAR_METHOD=$PRO_MAIN)
STAR_METHOD=$PRO_MAIN
export LD_LIBRARY_PATH=../../lib:$LD_LIBRARY_PATH

while :
do
PRO_NOW=`ps aux | grep $PRO_MAIN | grep -v grep | wc -l`
if [ $PRO_NOW -lt 1 ]; then
echo "-- start broker --"
$STAR_METHOD 2>/dev/null 1>&2 &
curtime=`date +"%Y-%m-%d %H:%M:%S"`
echo "$curtime $PRO_MAIN start" >> $PRO_PATH/tinfo.log
fi
sleep 5
done
exit 0

主要看红色部分。

　　第二步的start脚本如下：

#! /bin/bash
./middle_start.sh &

　　第三部的end脚本也很简单：

#!/bin/bash
#progress name
PRO_NAME="middle_start.sh"
BRK_NAME="broker"

ps -ef|grep $PRO_NAME |grep -v grep|awk '{print $2}'|xargs kill
echo "kill $PRO_NAME done!"
ps -ef|grep $BRK_NAME |grep -v grep|awk '{print $2}'|xargs kill -
echo "kill $BRK_NAME done"

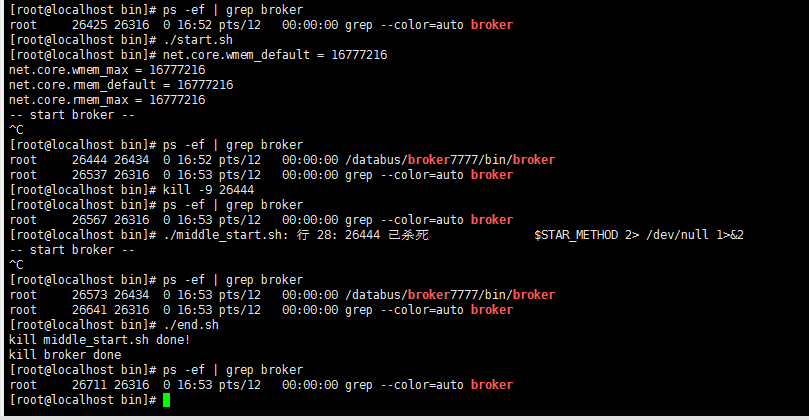
　　完成上面的步骤后，启动start脚本，ps查询broker已经运行，强行kill掉后broker仍然存在，已经是小强般的存在，执行end后broker销毁。