每日一题 LeetCode 486. 预测赢家 【递推】【前缀和】【动态规划】

题目链接

https://leetcode-cn.com/problems/predict-the-winner/

题目说明

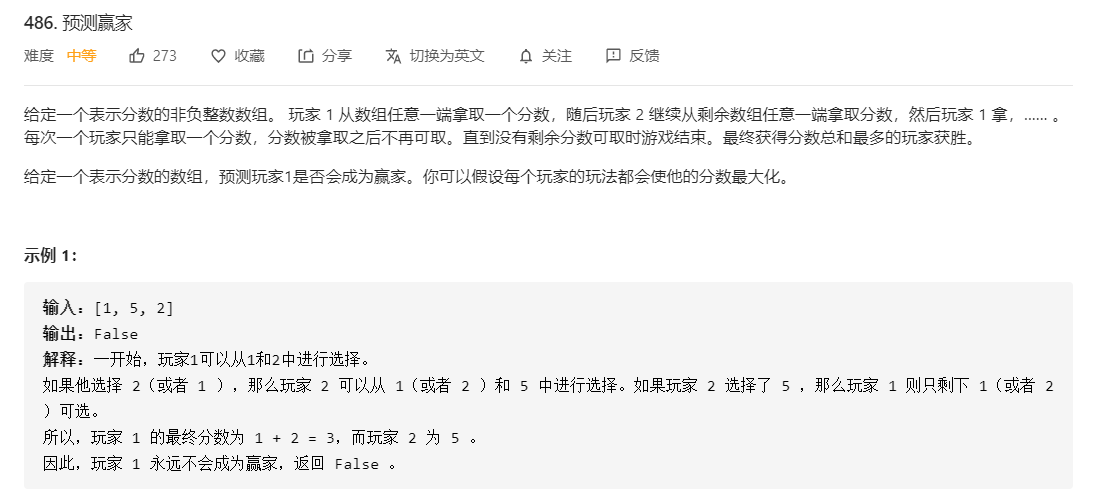
题解

主要方法：递推；动态规划；前缀和

解释说明：

1. 求前缀和 pre_nums ，pre_nums[0] = 0, pre_nums[1+i] = sum(nums[0……i])

2. 动态规划、递推：

   • 数据表示：设立二维数组dp，dp[i][j]表示区间 [i,j] 内先取者能取得的最大值。dpnums
   • 初始状态：遍历 nums 数组求得长度为 1 的区间 [i,i] 内的最大值，即 dp[i][i] = nums[i]
   • 动态方程：先后遍历长度l,起点i，dp[i][j] [i,j]内最大值 = pre_nums[j+1]-pre_nums[i] nums[i,j]的总和 - min(dp[i][j-1] 取尾端，则减去下一个人相应的最大值[i,j-1], dp[i+1][j]) 取首端，则减去下一个人相应的最大值[i+1,j]；

3. 数据输出：比较全部最大值与总和的一半 return dp[0][size-1] >= sum/2

代码示例：

class Solution:
    def PredictTheWinner(self, nums: List[int]) -> bool:
        size = len(nums)
        # 求前缀和
        pre_nums = [0]
        for i in range(size):
            pre_nums.append(pre_nums[-1]+nums[i])
        dp, tmp = nums[:], []
        # 动态规划，这里 dp 数组降维，重复使用
        for l in range(2, size+1):
            tmp.clear()
            for i in range(size - l + 1):
                tmp.append(pre_nums[i+l] - pre_nums[i] - min(dp[i], dp[i+1]))
            dp = tmp[:]
        return dp[0] >= pre_nums[-1]/2