▎前言　　

　　小编相当的菜，这篇博客难度稍高，所以有些可能不会带有证明，博客中更多的是定义。

　　我们将要学到的东西：

  • 复数
  • 暴力多项式乘法
  • DFT

　　当然，小编之前就已经写过一篇博客了，主要讲的就是基础多项式，如果你已经会了下面的内容就无需学了，否则请进入传送门。

  • 环和域
  • 多项式
  • 卷积
  • 多项式乘法
  • 多项式点值表示
  • 多项式的根
  • 单位根

▎复数

☞『引入』

　　其实小编早就应该讲复数了，但是上次忘了讲，那么这次一定要补上，好了，切入正题：

　　如果你信誓旦旦的在初中卷子上不判断根号下（√）的数是否是负数，那么你极有可能会被老师扇两巴掌，因为这是初中要注意的一大重点。　　

　　那么问题来了，究竟有没有诸如√-1这种数呢？其实是有的，初中阶段只会告诉你实数是什么，却不会告诉你还有诸如√-1这样的虚数（顾名思义，不存在的数）。

　　如果你是第一次见复数，那么你可能先想到的是单数和复数，其实不是这样的。

☞『定义』

　　我们把形如z=a+bi（a,b均为实数）的数称为复数，其中a称为实部，b称为虚部，i称为虚数单位。当z的虚部等于零时，常称z为实数；当z的虚部不等于零时，实部等于零时，常称z为纯虚数。复数域是实数域的代数闭包，即任何复系数多项式在复数域中总有根。 复数是由意大利米兰学者卡当在十六世纪首次引入，经过达朗贝尔、棣莫弗、欧拉、高斯等人的工作，此概念逐渐为数学家所接受。（copy自百度）

　　其实就是实数与虚数的统称啦。

☞『表示』

　　复数的表示字母是z，那么一个复数z可以表示为z=ai+b，其中a，b属于实数，i属于虚数，那么a称为虚部，b称为实部，i称为虚数单位。

　　例如i可以满足i2=1。

☞『运算』

　　复数和向量不同。

　　复数的运算和实数几乎一样，支持四则运算。

▎暴力多项式乘法

☞『算法』　　

　　在之前，我们已经知道了系数表示法和点值表示法的区别，假设有两个多项式分别长这样：

　　

　　

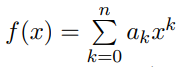
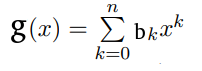
　　那么这两个多项式乘起来看着就心烦，那么怎么办呢？再看看点值表示法怎么样吧：

　　f(x)={(x0,f(x0),(x1,f(x1),(x2,f(x2),(x3,f(x3),…}

　　g(x)={(x0,g(x0),(x1,g(x1),(x2,g(x2),(x3,g(x3),…}

　　那么积是多少？

　　h(x)={(x0,f(x0)•g(x0),(x1,f(x1)•g(x1),(x2,f(x2)•g(x2),(x3,f(x3)•g(x3),…}

　　怎么样，点值表示法干题是不是爽到爆呢？

　　但是问题是：系数表示法如何变成点值表示法？

　　我们其实只需要n个数当做x带入得到f/g值即可。但是这样的做法无疑是O(n2)级别的，有时满足不了我们的需求，所以就要用到离散傅里叶变换了。

▎DFT

☞『引入』

　　这个算法有点不太对劲，百度介绍的好难呀。

　　我现在在质疑这个算法是不是处理物理的。

☞『定义』

　　离散傅里叶变换（DFT），是傅里叶变换在时域和频域上都呈现离散的形式，将时域信号的采样变换为在离散时间傅里叶变换（DTFT）频域的采样。在形式上，变换两端（时域和频域上）的序列是有限长的，而实际上这两组序列都应当被认为是离散周期信号的主值序列。即使对有限长的离散信号作DFT，也应当将其看作经过周期延拓成为周期信号再作变换。在实际应用中通常采用快速傅里叶变换以高效计算DFT。

　　我猜你也看不懂，其实就是快速系数转点值表示法呗。

☞『算法核心』

　　在之前，我们说的n个数带入转点值中的n个数是随便找的，所以出现一些棘手的问题很正常，就比如说当遇到高次的项时总会很难算。

　　所以我们如果能刻意的找到一些好算的x，那么就不难算出f/g的值了。

　　如果我们能找到一些x满足xk=1，那么就不必每个次方都算了。

　　想一想1和-1绝对是，考虑虚数的话i和-i也算。

　　那么我们可以画上这样一个平面直角坐标系：

　　

　　可是单单这么四个点显然是不够的，比如说n=8,傅里叶表示应该将这个圆平分成八份，取这样的八个点：

　　

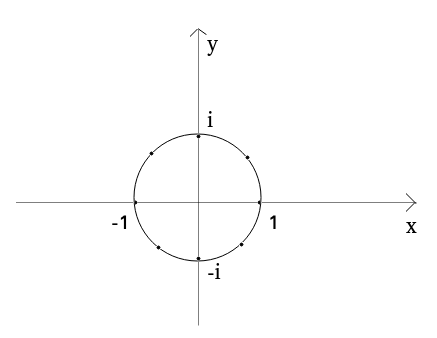
　　从（0,1）依次标号k：

　　

　　那么只要求出这八个点表示的复数即可，我们记标号k的点表示的复数为ωnk，那么就有：

　　

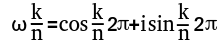
　　这里面的东西都可以算出来的。

【算法•日更•第四十二期】离散傅里叶变换（DFT）的更多相关文章

  1. 【算法•日更•第三十二期】教你用出windows体验的Linux

    ▎前言 小编昨天闲的不行,就装了一个linux系统,linux的发行版很多,小编认为ubuntu很好用,于是就在使用ubuntu. 没错,我现在就在使用ubuntu来写博客. 刚才还装了一个QQ,不过 ...

  2. 【算法•日更•第四十三期】QQ for linux

    废话不多说,直接看一张图: 没错,这是QQ,但是这有什么稀奇的?但是在Linux上使用QQ就很稀奇了. 众所周知,腾讯早就已经对Linux下的QQ和微信停止了服务,即便是网页版也不能用,通信这一直是小 ...

  3. 【算法•日更•第五十四期】知识扫盲：什么是operator？

    ▎前言 这个东西和迭代器长的很像,但是比迭代器常见的多. 今天就来浅谈operator. ▎定义 operator是C#.C++和pascal的关键字,它和运算符一起使用,表示一个运算符函数,理解时应 ...

  4. 【算法•日更•第三十九期】迭代加深搜索：洛谷SP7579 YOKOF - Power Calculus 题解

    废话不多说,直接上题: SP7579 YOKOF - Power Calculus 题意翻译 (略过没有营养的题干) 题目大意: 给出正整数n,若只能使用乘法或除法,输出使x经过运算(自己乘或除自己, ...

  5. 【算法•日更•第三十五期】FF算法优化：EK算法

    ▎写在前面 FF算法传送门 之前我们已经学过了FF算法(全称Ford-Fulkerson算法)来找最大流,但是这种算法仍有诸多不对的地方. 其实这种算法存在着严重的效率的问题,请看下面的图: 以这个图 ...

  6. 【算法•日更•第五十期】二分图（km算法）

    ▎前言 戳开这个链接看看,惊不惊喜,意不意外?传送门. 没想到我的博客竟然被别人据为己有了,还没办法投诉. 这年头写个博客太难了~~~ 之前小编写过了二分图的一些基础知识和匈牙利算法,今天来讲一讲km ...

  7. 【算法•日更•第三十一期】KMP算法

    ▎前言 这次要讲的HMP算法KMP算法很简单,是用于处理字符串的,之前一直以为很难,其实也不过如此(说白了就是优化一下暴力). ▎处理的问题 通常处理的问题是这样的:给定两个字符串s1和s2,其中s1 ...

  8. 【算法•日更•第四十七期】Mac与windows系统的差别

    小编最近装了个Mac系统,因为小编已经有笔记本可以用linux了,所以就决定在台式机上装个双系统,结果一不小心把Mac装在C盘上了,哎,说多了都是泪啊. 其实用了Mac之后才发现windows特别好用 ...

  9. 【算法•日更•第三十期】区间动态规划：洛谷P4170 [CQOI2007]涂色题解

    废话不多说,直接上题:  P4170 [CQOI2007]涂色 题目描述 假设你有一条长度为5的木版,初始时没有涂过任何颜色.你希望把它的5个单位长度分别涂上红.绿.蓝.绿.红色,用一个长度为5的字符 ...

随机推荐

  1. websphere8.5配置db2数据源

    websphere8.5配置db2数据源 1. 打开websphere控制台  2.进入websphere变量页面  3. 进入DB2UNIVERSAL_JDBC_DRIVER_NATIVEPATH变 ...

  2. 基于Python爬虫采集天气网实时信息

      相信小伙伴们都知道今冬以来范围最广.持续时间最长.影响最重的一场低温雨雪冰冻天气过程正在进行中.预计,今天安徽.江苏.浙江.湖北.湖南等地有暴雪,局地大暴雪,新增积雪深度4-8厘米,局地可达10- ...

  3. 图论相关知识（DFS、BFS、拓扑排序、最小代价生成树、最短路径）

    图的存储 假设是n点m边的图: 邻接矩阵:很简单,但是遍历图的时间复杂度和空间复杂度都为n^2,不适合数据量大的情况 邻接表:略微复杂一丢丢,空间复杂度n+m,遍历图的时间复杂度为m,适用情况更广 前 ...

  4. async基本使用

    async函数在使用上很简单,我们来看一下下面的例子 async function add(a,b){ return a+b } add(1,2).then((res) =>{ consoel. ...

  5. Mosquitto的搭建（websocket、ssl、auth-plug）及坑点总结

    Mosquitto的搭建及坑点总结 主要讲述的是eclipse-mosquitto的C语言版本的搭建,主要是为了从1.4.15版本升级到1.6.9,为解决一些webSocket和数据格式问题. 因为根 ...

  6. 萌新学渗透系列之Hack The Box_Devel

    我将我的walkthrough过程用视频解说的形式记载 视频地址https://www.bilibili.com/video/BV1Ck4y1B7DB 一是因为看我视频的后来者应该都是刚入门的新手,视 ...

  7. PHP atanh() 函数

    实例 返回不同数的反双曲正切: <?phpecho(atanh(M_PI_4) . "<br>");echo(atanh(0.50) . "<br ...

  8. Skill 中的通用输出格式规范

    https://www.cnblogs.com/yeungchie/ Skill中的通用输出格式规范 Common Output Format Specifications Format Specif ...

  9. AGC 043 C - Giant Graph SG函数 dp 贪心

    LINK:Giant Graph 神仙题目. 容易发现在图中选择某个点的贡献为\(10^{18\cdot(x+y+z)}\) 这等价于多选一个点多大一点就多乘了一个\(10^{18}\) 所以显然是贪 ...

  10. 不用注入方式使用Spring管理的对象中的方法，神奇

    在小冷工作中遇到这么一个小问题,当你的业务层对象交给spring管理之后,在普通的类中调用这个类中的方法时候,会有个问题这个类在调用时候会一直返回一个null,而且还会抛出一个空指针异常. 小冷在遇到 ...