存在！

  • 首先我们知道int的取值范围是：
  • -2147483648~2147483647，最高位为符号位
  • 2147483647的二进制为：01111111 11111111 11111111 11111111
  • 那么2147483647+1，计算机的底层逻辑是二进制相加：
    • 01111111     11111111     11111111      11111111
    • 00000000　00000000　00000000   00000001
    • 10000000    00000000    00000000   00000000
    • =-2147483648

代码验证

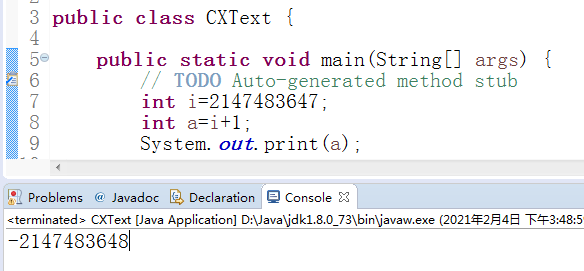
这里是拿int类型32位做例子，可以看出，当最高位为1时，它既是符号位，也是数值位

进一步推理是否存在11111111     11111111     11111111      11111111这样的数?

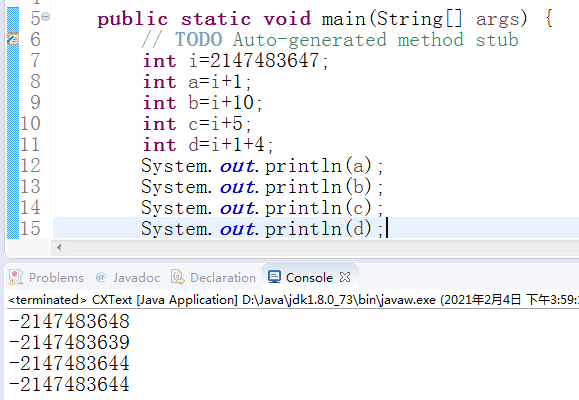
答案：不存在，可以看出，当为最小负数时，会先判断是否达到最小负数，然后再次相加

即：2147483647+5=

(2147483647+1)+4=

-2147483648+4=

-2147483644

 

java中是否存在i+1<i?的更多相关文章

  1. java中的锁

    java中有哪些锁 这个问题在我看了一遍<java并发编程>后尽然无法回答,说明自己对于锁的概念了解的不够.于是再次翻看了一下书里的内容,突然有点打开脑门的感觉.看来确实是要学习的最好方式 ...

  2. java中的字符串相关知识整理

    字符串为什么这么重要 写了多年java的开发应该对String不陌生,但是我却越发觉得它陌生.每学一门编程语言就会与字符串这个关键词打不少交道.看来它真的很重要. 字符串就是一系列的字符组合的串,如果 ...

  3. Java中的Socket的用法

                                   Java中的Socket的用法 Java中的Socket分为普通的Socket和NioSocket. 普通Socket的用法 Java中的 ...

  4. java中Action层、Service层和Dao层的功能区分

    Action/Service/DAO简介: Action是管理业务(Service)调度和管理跳转的. Service是管理具体的功能的. Action只负责管理,而Service负责实施. DAO只 ...

  5. Java中常用集合操作

    一.Map 名值对存储的. 常用派生类HashMap类 添加: put(key,value)往集合里添加数据 删除: clear()删除所有 remove(key)清除单个,根据k来找 获取: siz ...

  6. java中的移位运算符：<<,>>,>>>总结

    java中有三种移位运算符 <<      :     左移运算符,num << 1,相当于num乘以2 >>      :     右移运算符,num >& ...

  7. 关于Java中进程和线程的详解

    一.进程:是程序的一次动态执行,它对应着从代码加载,执行至执行完毕的一个完整的过程,是一个动态的实体,它有自己的生命 周期.它因创建而产生,因调度而运行,因等待资源或事件而被处于等待状态,因完成任务而 ...

  8. Java中的进程和线程

     Java中的进程与线程 一:进程与线程 概述:几乎任何的操作系统都支持运行多个任务,通常一个任务就是一个程序,而一个程序就是一个进程.当一个进程运行时,内部可能包括多个顺序执行流,每个顺序执行流就是 ...

  9. Java中的进程与线程（总结篇）

    详细文档: Java中的进程与线程.rar 474KB 1/7/2017 6:21:15 PM 概述: 几乎任何的操作系统都支持运行多个任务,通常一个任务就是一个程序,而一个程序就是一个进程.当一个进 ...

  10. 初探java中this的用法

    一般this在各类语言中都表示“调用当前函数的对象”,java中也存在这种用法: public class Leaf { int i = 0; Leaf increment(){ i++; retur ...

随机推荐

  1. swap交换2变量

    #define swap(x,y) {(x)=(x)+(y); (y)=(x)-(y); (x)=(x)-(y);} void swap(int i, int offset){ int temp; t ...

  2. 怎样将Sublime Text 设置成中文版（完整教程）

    1.打开Sublime Text,使用快捷键Shift+Ctrl+P,弹出查找栏,如图: 2.在搜索框中输入关键字 install ,出现下拉选项,点击选择其中的:Package Control: I ...

  3. Flink-v1.12官方网站翻译-P003-Real Time Reporting with the Table API

    利用表格API进行实时报告 Apache Flink提供的Table API是一个统一的.关系型的API,用于批处理和流处理,即在无边界的.实时的流或有边界的.批处理的数据集上以相同的语义执行查询,并 ...

  4. left join与inner join

    举例a.b表: bId bNum 1 20 2 30 aId aNum 1 10 2 20 3 30 left join以左表为准 select * from a left join b on a.a ...

  5. 组合数取模及Lucas定理

    引入: 组合数C(m,n)表示在m个不同的元素中取出n个元素(不要求有序),产生的方案数.定义式:C(m,n)=m!/(n!*(m-n)!)(并不会使用LaTex QAQ). 根据题目中对组合数的需要 ...

  6. 【uva 1658】Admiral（图论--网络流 最小费用最大流）

    题意:有个N个点M个边的有向加权图,求1~N的两条不相交路径(除了起点和终点外没有公共点),使得权和最小. 解法:不相交?也就是一个点只能经过一次,也就是我后面博文会讲的"结点容量问题&qu ...

  7. BKDR字符串哈希

    BKDR字符串哈希 bkdrhash冲突的可能性非常小,但是由于\(hash\)值非常大不能映射到哈希数组地址上,所以可以通过取余,用余数作为索引地址.但这样做造成了可能的地址冲突. #include ...

  8. GO - go mod使用原理

    Go Module 依赖管理 go mod使用 原理及使用ref: https://xuanwo.io/2019/05/27/go-modules/ go module的稳定路径: https://l ...

  9. C++ inline与operator

    title: C++ inline与operator date: 2020-03-10 categories: c++ tags: [c++] inline修饰符,operator关键字 1.inli ...

  10. codeforces 10C Digital Root（非原创）

    Not long ago Billy came across such a problem, where there were given three natural numbers A, B and ...