FLOYD判圈

转载一篇博客：http://blog.csdn.net/javasus/article/details/50015687

Floyd判圈算法(Floyd Cycle Detection Algorithm)，又称龟兔赛跑算法(Tortoise and Hare Algorithm)。该算法由美国科学家罗伯特·弗洛伊德发明，是一个可以在有限状态机、迭代函数或者链表上判断是否存在环，求出该环的起点与长度的算法。

如果有限状态机、迭代函数或者链表上存在环，那么在某个环上以不同速度前进的2个指针必定会在某个时刻相遇。同时显然地，如果从同一个起点(即使这个起点不在某个环上)同时开始以不同速度前进的2个指针最终相遇，那么可以判定存在一个环，且可以求出2者相遇处所在的环的起点与长度。

算法描述

如果有限状态机、迭代函数或者链表存在环，那么一定存在一个起点可以到达某个环的某处(这个起点也可以在某个环上)。

初始状态下，假设已知某个起点节点为节点S。现设两个指针t和h，将它们均指向S。

接着，同时让t和h往前推进，但是二者的速度不同：t每前进1步，h前进2步。只要二者都可以前进而且没有相遇，就如此保持二者的推进。当h无法前进，即到达某个没有后继的节点时，就可以确定从S出发不会遇到环。反之当t与h再次相遇时，就可以确定从S出发一定会进入某个环，设其为环C。

如果确定了存在某个环，就可以求此环的起点与长度。

计算环长度

上述算法刚判断出存在环C时，显然t和h位于同一节点，设其为节点M。显然，仅需令h不动，而t不断推进，最终又会返回节点M，统计这一次t推进的步数，显然这就是环C的长度。

计算环起点

为了求出环C的起点，只要令h仍位于节点M，而令t返回起点节点S。随后，同时让t和h往前推进，且保持二者的速度相同：t每前进1步，h前进1步。持续该过程直至t与h再一次相遇，设此次相遇时位于同一节点P，则节点P即为从节点S出发所到达的环C的第一个节点，即环C的一个起点。

链表起点为节点S，环起点为节点P，t和h相遇时位于同一节点M，S和P之间的距离为p，P和M之间的距离为m，环长为C，这里两点之间的距离是指从一点走多少步可以到点另外一点。

当t和h相遇时，

t走的步数，step = p + m + a * C，a表示相遇时t走的圈数

h走的步数，2 * step = p + m + b * C，b表示相遇时h走的圈数

两者相减：step = (b - a) * C = p + m + a * C，由此可知t走的步数是环C的倍数，即 p + m 刚好是环长度C的倍数。

t和h在M处相遇，为了计算环C的起点，令h仍位于节点M，而令t返回起点S，随后，同时让t和h往前推进，且保持两者的速度相同：t每前进1步，h前进1步。持续该过程直至t与h再一次相遇，则它们此次相遇时一定位于环的起始节点P。为什么它们此次相遇时一定在环起始节点呢？

t走了p步到达P，h在环C上p步在哪呢？h从M处出发走了p步，相对于环起始位置，h走过的距离是 m + p，而m + p刚好是环长度C的倍数，即h此时也位于环起始节点处，即t和h在P处相遇。据此就可以计算出环起始节点的位置。

算法复杂度

时间复杂度

注意到当指针t到达环C的一个起点节点P时(此时指针h显然在环C上)，之后指针t最多仅可能走1圈。若设节点S到P距离为，环C的长度为，则时间复杂度为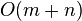，是线性时间的算法。

空间复杂度

仅需要创立指针t、指针h，保存环长n、环的一个起点P。空间复杂度为，是常数空间的算法。

应用

对于有限状态机与链表，可以判断从某个起点开始是否会返回到访问过运行过程中的某个状态和节点。

对于迭代函数，可以判断其是否存在周期，以及求出其最小正周期。

 1 int *head = list.GetHead();
 2 if (head != null) {
 3     int *fastPtr = head;
 4     int *slowPtr = head;
 5
 6     bool isCircular = true;
 7
 8     do
 9     {
10         if (fastPtr->Next == null || fastPtr->Next->Next == null) //List end found
11         {
12             isCircular = false;
13             break;
14         }
15
16         fastPtr = fastPtr->Next->Next;
17         slowPtr = slowPtr->Next;
18     } while (fastPtr != slowPtr);
19     //确定环的起点
20     slowPtr = head;
21     while(slowPtr != fastPtr)
22     {
23         slowPtr = slowPtr->Next;
24         fastPtr = fastPtr->Next;
25     }
26     cout<<"the starting point of the cycle is "<<slowPtr<<endl;
27 }