python线性回归

一.理论基础

1.回归公式
　　对于单元的线性回归，我们有：f(x) = kx + b 的方程(k代表权重，b代表截距）。
　　对于多元线性回归，我们有：
　　　
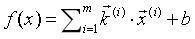
　　或者为了简化，干脆将b视为k₀·x₀,，其中k₀为1，于是我们就有：
　　　
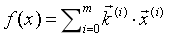
２.损失函数

3.误差衡量
MSE,RMSE,MAE越接近于0越好，R方越接近于1越好。

MSE平均平方误差(mean squared error)
　　　

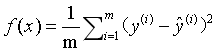
RMSE，是MSE的开根号
　　
MAE平均绝对值误差(mean absolute error)
　　　

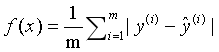
Ｒ方
　　　

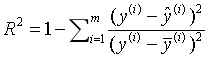
其中y_hat是预测值。

二.代码实现

本次，我们将用iris数据集实现单元线性回归的机器学习，使用boston数据集实现多元线性回归的机器学习。在python中，单元线性回归与多元线性回归的操作完全一样，这里只是为了演示而将其一分为二。
1.鸢尾花花瓣长度与宽度的线性回归

# 导入鸢尾花数据集
from sklearn.datasets import load_iris
# 导入用于分割训练集和测试集的类
from sklearn.model_selection import train_test_split
# 导入线性回归类
from sklearn.linear_model import LinearRegression
import numpy as np

iris = load_iris()

'''
iris数据集的第三列是鸢尾花长度，第四列是鸢尾花宽度
x和y就是自变量和因变量
reshape(-1,1)就是将iris.data[:,3]由一维数组转置为二维数组,
以便于与iris.data[:,2]进行运算
'''
x,y = iris.data[:,2].reshape(-1,1),iris.data[:,3]
lr = LinearRegression()

'''
train_test_split可以进行训练集与测试集的拆分，
返回值分别为训练集的x，测试集的x，训练集的y，测试集的y,
分别赋值给x_train,x_test,y_train,y_test,
test_size:测试集占比
random_state:选定随机种子
'''
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size = 0.25,random_state = 0)
# 利用训练集进行机器学习
lr.fit(x_train,y_train)
# 权重为lr.coef_
# 截距为lr.intercept_
# 运用训练出来的模型得出测试集的预测值
y_hat = lr.predict(x_test)
# 比较测试集的y值与预测出来的y值的前5条数据
print(y_train[:5])
print(y_hat[:5])

# 评价模型的准确性,用测试集来评价
# 导入分别用于求MSE,MAE和R方的包
from sklearn.metrics import mean_squared_error,mean_absolute_error,r2_score
# 求解MSE
print('MSE:',mean_squared_error(y_test,y_hat)）
# 求解RMSE,是MSE的开根号
print('RMSE:',np.sqrt(mean_squared_error(y_test,y_hat))
# 求解MAE
print('MAE:',mean_absolute_error(y_test,y_hat))
# 求解R方,有两种方法，注意lr.score的参数是x_test,y_test
print('R方:',r2_score(y_test,y_hat))
print('R方:',lr.score(x_test,y_test))

# 导入matplotlib模块，进行可视化
from matplotlib import pyplot as plt
plt.rcParams['font.family'] = 'SimHei'
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.size'] = 15
plt.figure(figsize = (20,8))
# 训练集散点图
plt.scatter(x_train,y_train,color = 'green',marker = 'o',label = '训练集')
# 测试集散点图
plt.scatter(x_test,y_test,color = 'orange',marker = 'o',label = '测试集')
# 回归线
plt.plot(x,lr.predict(x),'r-')
plt.legend()
plt.xlabel('花瓣长度')
plt.ylabel('花瓣宽度')

就这样画出了一张很丑的图，如果想画更精美的图或者其他方面的比较，各位读者不妨自己去试一试吧。

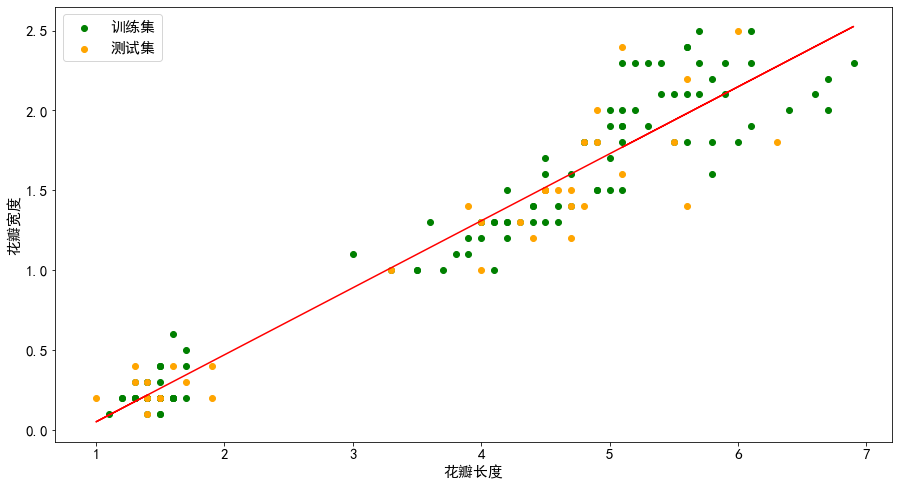
　　刚刚我们做了对鸢尾花花瓣长度和宽度的线性回归，探讨长度与宽度的关系，探究鸢尾花的花瓣宽度受长度变化的趋势是怎么样的。但是在现实生活当中的数据是十分复杂的，像这种单因素影响的事物是比较少的，我们需要引入多元线性回归来对多个因素的权重进行分配，从而与复杂事物相符合。

2.boston房价预测（多元线性回归）

呐，boston数据集的介绍在这里了，我就不详细介绍了
现在，我们要探讨boston当中每一个因素对房价的影响有多大，这就是一个多因素影响的典型例子。

import pandas as pd
import numpy as np
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
boston = load_boston()
# lr继承LinearRegression类
lr = LinearRegression()
# 因为boston.data本身就是二维数组，所以无需转置,boston.target是房价
x,y = boston.data,boston.target
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size = 0.15,random_state = 0)
lr.fit(x_train,y_train)
# 显示权重，因为有很多因素，所以权重也有很多个
print(lr.coef_)
# 显示截距
print(lr.intercept_)
y_hat = lr.predict(x_test)

# 模型评判仍然是用那几个包，这里不再赘述。

结果如下，可以发现每一个因素都有相应的权重。

[-1.24536078e-01 4.06088227e-02 5.56827689e-03 2.17301021e+00
-1.72015611e+01 4.02315239e+00 -4.62527553e-03 -1.39681074e+00
2.84078987e-01 -1.17305066e-02 -1.06970964e+00 1.02237522e-02
-4.54390752e-01]
36.09267761760974

本文的文字及图片来源于网络,仅供学习、交流使用,不具有任何商业用途,如有问题请及时联系我们以作处理

想要获取更多Python学习资料可以加
QQ:2955637827私聊
或加Q群630390733
大家一起来学习讨论吧！