RepVGG

RepVGG: Making VGG-style ConvNets Great Again

作者：elfin  
资料来源：RepVGG论文解析

---

目录

• 1、摘要
• 2、背景介绍
• 3、相关工作
  • 3.1 单分支到多分支
  • 3.2 单分支模型的高效训练
  • 3.3 模型参数重构
  • 3.4 Winograd(威诺格拉德)卷积
• 4、由结构参数重构技术构建RepVGG
  • 4.1 简单即快速、内存使用经济、灵活
  • 4.2 训练时的多分支结构
  • 4.3 推理时的模型参数重构
  • 4.4 结构规格

---

Top
 --- 
Bottom

1、摘要

​ 我们提出了一种简单而强大的卷积神经网络结构，它具有类似VGG的推理结构，仅由3×3卷积和ReLU组成，而训练模型具有多分支拓扑结构。这种训练和推理结构的解耦是通过一种结构参数重构技术(structural re-parameterization)来实现的，因此该模型被命名为RepVGG。在ImageNet上，RepVGG达到了80%以上的top-1精度，据我们所知，这是第一次使用普通模型。在nvidia1080TI gpu上，RepVGG模型的运行速度比ResNet-50快83%，比ResNet-101快101%，精度更高，与EfficientNet和RegNet等最先进的模型相比，显示出良好的精度-速度折衷。

​ 项目地址：https://github.com/megvii-model/RepVGG

​ pytorch版本：https://github.com/DingXiaoH/RepVGG

---

Top
 --- 
Bottom

2、背景介绍

​ 卷积神经网络（ConvNets）已成为解决许多问题的主流方法。VGG在图像识别方面取得了巨大的成功，但是它仅使用了一个由conv、ReLU和pooling组成的简单体系结构。随着Inception、ResNet和DenseNet的出现，许多研究兴趣转移到了设计良好的体系结构上，使得模型变得越来越复杂。最近一些强大的架构是通过自动或手动的架构搜索，或者在一个基本架构上搜索一个复合缩放策略来获得的。

​ 虽然许多复杂的卷积网络比简单的卷积网络提供更高的精度，但缺点是显著的：

• (1) 复杂的多分支设计（如ResNet中的残差分支 和 Inception中的分支级联）使得模型难以实现和定制，降低了推理速度，降低了内存利用率。
• (2) 一些组件增加了内存访问成本，并且缺乏对各种设备的支持（例如，Xception和MobileNets 中的depthwise 以及ShuffleNets中的通道shuffle。

​ 由于影响推理速度的因素很多，浮点运算（FLOPs）的数量并不能准确反映实际速度。尽管一些新的模型比老式的VGG和ResNet有更低的浮点运算，但是他们可以运行速度并不快。下表展示了运行速度的变换：

​

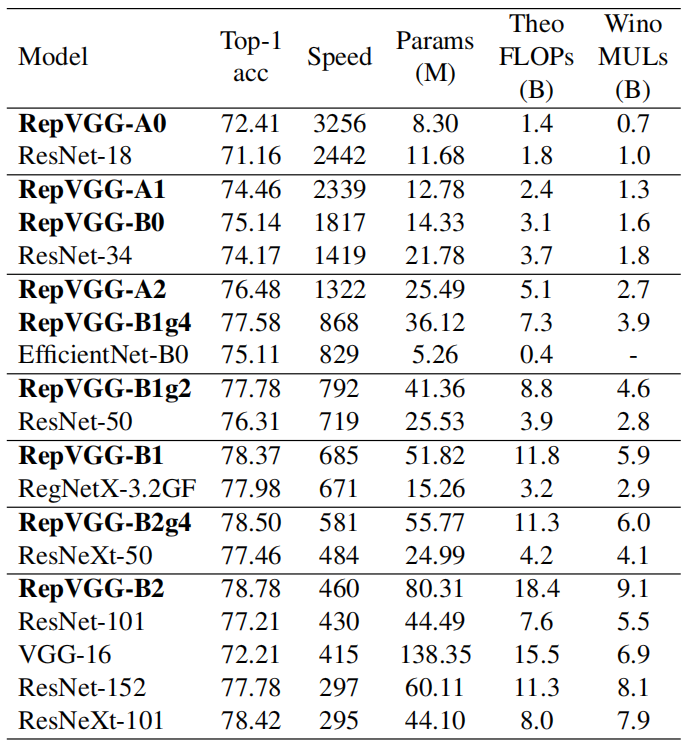
因此，VGG和ResNets的原始版本仍然大量用于学术界和工业界的实际应用。

​ 在本文中，我们提出了RepVGG，这是一种VGG风格的结构，它优于许多复杂的模型，如图所示：

​

RepVGG的优点有：

• 该模型有一个类似VGG的拓扑结构，没有任何分支。也就是说，每一层都将其前一层的输出作为输入，并将输出输入到其后一层。
• 模型仅使用 \(3 \times 3\) 的卷积结构和\(ReLU\)激活。
• 具体的架构（包括特定的深度和层宽度）是没有自动搜索、手动细化、复合缩放，也没有其他繁重设计的实例化。

​ 普通模型要达到与多分支体系结构相当的性能水平是一个挑战。一种解释是，多分支拓扑（例如ResNet）使模型成为许多较浅模型的隐式集合，因此训练多分支模型可以避免梯度消失问题。

​ 由于多分支结构的优点都是用于训练，缺点是不希望用于推理，因此我们提出通过结构参数重构将训练多分支结构和推理结构解耦，即通过参数转换将结构从一个结构转换为另一个结构。具体而言，网络结构与一组参数耦合，例如，conv层由四阶核张量表示。如果某个结构的参数可以转换成另一个结构耦合的另一组参数，就可以等价地用后者代替前者，从而改变整个网络结构。

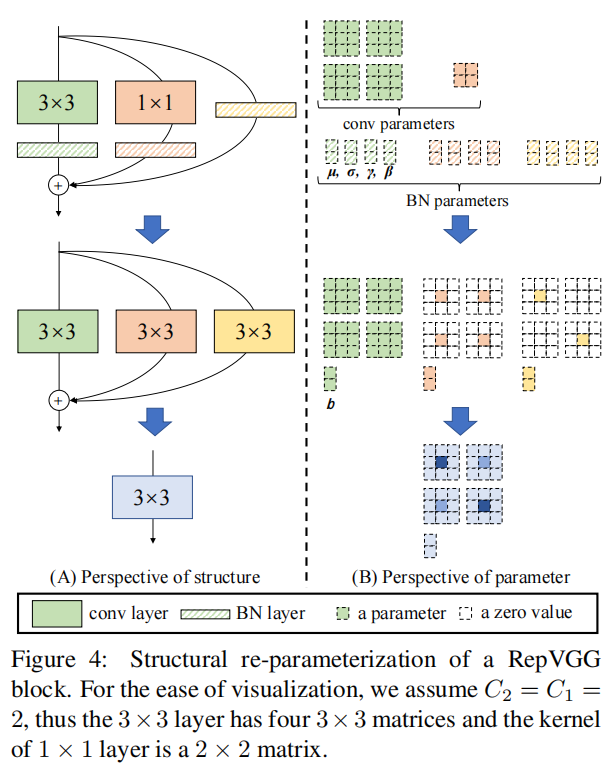
​ 具体地说，我们使用identity和1×1分支构造RepVGG的训练结构，这是受ResNet启发的，但不同的方法是通过结构参数重构去除分支（如下图所示）。经过训练后，我们用简单代数进行变换，因为一个恒等分支可以看作退化的1×1变换，后者可以进一步看作退化的3×3变换，所以我们可以用原3×3核的训练参数构造一个3×3核，identity分支和1×1分支和批量规范化（BN）层。因此，转换后的模型是一个3×3 conv层的堆栈，可以保存以供测试和部署。

​

​

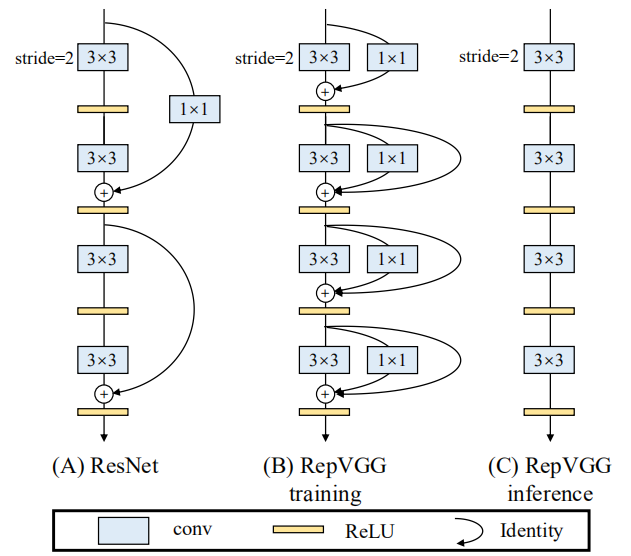
​ 值得注意的是，RepVGG的推理主体只涉及一种操作类型：3×3 conv，然后是ReLU，这使得RepVGG在gpu等通用计算设备上运行得很快。更好的是，RepVGG允许专用硬件实现更高的速度，因为考虑到芯片大小和功耗，我们需要的操作类型越少，我们可以集成到芯片上的计算单元就越多。即，专门用于RepVGG的推理芯片可以具有大量的3×3-ReLU单元和更少的存储器单元（因为普通拓扑是存储器经济的，如图3所示）。我们的贡献总结如下：

• 我们提出了RepVGG，这是一种简单的体系结构，与现有技术相比，它具有良好的速度精度折衷。
• 我们提出使用结构参数重构来将训练多分支拓扑与推理结构解耦。
• 我们已经证明了RepVGG在图像分类和语义分割方面的有效性，以及它的效率和易实现性。

​

---

Top
 --- 
Bottom

3、相关工作

3.1 单分支到多分支

​ VGG网络在ImgNet竞赛中获得最优的性能后，许多新的创新将其精确度进一步提高。如：GoogLeNet、Inception采用多分支结构； ResNet使用了简单的二分支结构；DenseNet通过连接低层和多个高层，使得拓扑结构更加复杂。神经结构搜索（NAS）和人工设计空间设计可以产生性能更高的网络，但代价是巨大的计算资源或人力。一些大版本的NAS生成模型甚至不能在普通gpu上训练，因此限制了其应用。除了实现的不便外，复杂模型也会降低并行度，从而降低推理速度。

---

Top
 --- 
Bottom

3.2 单分支模型的高效训练

​ 有人试图训练没有分支的网络。然而，以往的工作主要是为了使非常深的模型收敛到合理的精度，但并没有取得比复杂模型更好的性能。因此，这些方法和模型既不简单，也不实用。例如，提出了一种初始化方法来训练极深的平面网络。采用基于平均场理论的训练方案，在MNIST上训练了10000层网络，训练精度达到99%，在CIFAR-10上训练精度达到82%。尽管这些模型并不实用（即使LeNet-5在MNIST上的准确率也能达到99.3%，VGG-16在CIFAR-10上的准确率也能达到93%以上），但其理论贡献是深刻的。最近的一项工作[24]结合了几种技术，包括 Leaky ReLU、最大范数和谨慎初始化。在ImageNet上，一个具有147M参数的普通ConvNet可以达到74.6%的top-1精度，比其报告的基线（ResNet-101，76.6%，45M参数）低2%。值得注意的是，本文不仅证明了普通模型可以很好地收敛，而且不打算像resnet那样训练极深的convnet。相反，我们的目标是建立一个具有合理深度和良好精度-速度权衡的简单模型，该模型可以简单地用最常见的组件（如正则conv和BN）和简单代数实现。

---

Top
 --- 
Bottom

3.3 模型参数重构

​ DiracNet[38]是一种与我们相关的参数重构方法。它通过把一个卷积层的卷积核编码为：

\[\hat{W} = diag(\vec{a})I + diag(\vec{b})W_{norm}
\]

其中\(\hat{W}\) 是卷积的最终权重，是一个四阶的张量矩阵；\(W_{norm}\) 是标准化的kernel，\(\vec{a}\)、\(\vec{b}\) 是需要学习的向量。与残差神经网络相比，在性能方面，DiracNet在CIFAR-100数据集上要低 \(2.29\%\) ，ImageNet数据集上要低\(0.62\%\)。

DiracNet模型与RepVGG的差异为：

• 我们的结构参数重构是通过一个具体结构的实际数据流来实现的，这个具体结构以后可以转换成另一个结构，而DiracNet仅仅使用另一个转换核的数学表达式，以便于优化。也就是说，一个结构参数重构的平面模型是一个实时训练的多分支模型，而DiracNet不是。
• DiracNet的性能高于通常参数化的普通模型，但低于可比较的ResNet，而RepVGG模型的性能远远优于ResNet。

​ Asym Conv Block（ACB）[9]采用非对称Conv来加强规则Conv的“骨架”，这可以看作是结构参数重构的另一种形式，因为它将训练的块转换为Conv。与我们的方法相比，不同之处在于，ACB是为组件级改进而设计的，并在任何体系结构中用作conv层的替换，而我们的结构重新参数化对于训练普通convnet非常关键，如第4.2节所示。

---

Top
 --- 
Bottom

3.4 Winograd(威诺格拉德)卷积

​ RepVGG只使用3×3 conv，因为它在GPU和CPU上都被一些现代计算库（如NVIDIA cuDNN[1]和Intel MKL[16]）高度优化。下表显示了在1080TI GPU上用cudnn7.5.0测试的理论FLOPS、实际运行时间和计算密度（以每秒Tera(兆兆)浮点运算（TFLOPS）为单位）。结果表明，3×3conv的理论计算密度约为4倍，表明理论总的FLOPs数不能代表不同体系结构的实际速度。

加速3×3 conv的一个经典算法是Winograd算法[18]（仅当步长为1时），它得到了cuDNN和MKL等库的良好支持（默认情况下启用）。例如，使用标准\(F(2 \times 2, 3 \times 3)\)的Winograd，3×3 conv的乘法量（mul）减少到原来的\(\frac{4}{9}\)。由于乘法要比加法耗时得多，所以我们计算Muls来度量Winograd支持下的计算开销(后面会提到)。请注意，特定的计算库和硬件决定是否对每个操作符使用Winograd，因为小规模的卷积可能不会由于内存开销而加速。

---

Top
 --- 
Bottom

4、由结构参数重构技术构建RepVGG

4.1 简单即快速、内存使用经济、灵活

使用简单convnet至少有三个原因：它们速度快、内存经济且灵活。

Fast 许多最近的多分支架构的理论 FLOPs比VGG低，但可能运行得不快。 VGG-16的 FLOPs是EffificientNet-B3的8.4倍，但是运行速度却是其1.8倍，这意味着前者的计算密度为后者的15倍。除了Winograd conv带来的加速外，FLOPs和速度之间的差异可归因于两个重要因素，它们对速度有相当大的影响，但FLOPs没有考虑到这两个因素：内存访问成本（MAC）和并行度[23]。如：虽然所需的分支加法或级联计算可以忽略不计，但MAC是重要的。此外，MAC在分组卷积中占很大一部分时间。另一方面，在相同的FLOPs条件下，一个高并行度的模型比另一个低并行度的模型要快得多。由于多分支拓扑结构被广泛应用于初始和自动生成的体系结构中，因此使用多个小的操作符来代替几个大的操作符。先前的一项工作[23]报告说，NASNET-A[42]中的分段运算符（即单个conv或池操作在一个构建块中的数目）为13，这对GPU等具有强大并行计算能力的设备不友好，并引入额外的开销，如内核启动和同步。相反，在resnet中，这个数字是2或3，我们将它设为1：单个conv。

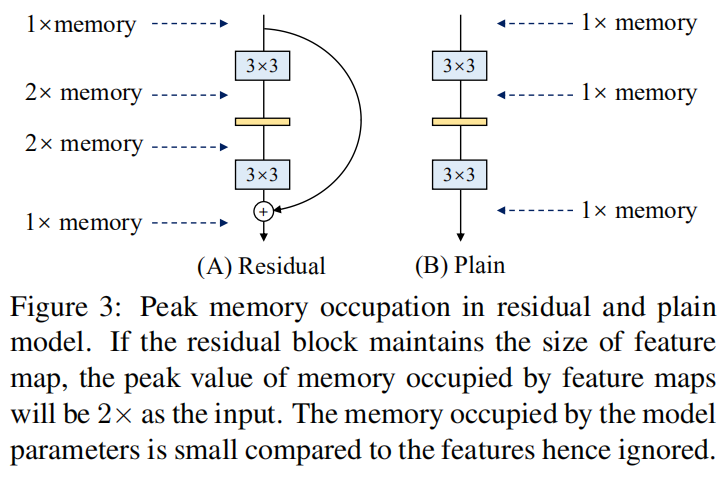
Memory-economical 多分支拓扑的内存效率很低，因为每个分支的结果都需要保留到加法或级联之后，这大大提高了内存占用的峰值。剩余块的输入需要保持，直到添加为止。假设块保持特征图大小，则内存占用峰值为输入的两倍。相反，普通拓扑允许在操作完成时立即释放特定层的输入占用的内存。在设计专用硬件时，一个普通的ConvNet允许深度内存优化并降低内存单元的成本，这样我们就可以将更多的计算单元集成到芯片上。

Flexible 多分支拓扑对体系结构规范施加了约束。ResNet要求conv层被组织为残差块，这限制了灵活性，因为每个残差块的最后一个conv层必须产生相同形状的张量，否则快捷加法就没有意义。更糟的是，多分支拓扑限制了channel修剪[20,12]的应用，这是一种去除一些不重要通道的实用技术，一些方法可以通过自动发现每层的适当宽度来优化模型结构[7]。然而，多分支模型使得剪枝变得棘手，并导致性能显著下降或加速比低[6，20，8]。相反，简单的体系结构允许我们根据需求自由配置每个conv层，并进行删减以获得更好的性能效率权衡。

---

Top
 --- 
Bottom

4.2 训练时的多分支结构

​ 普通网络有很多优点，但有一个致命的缺点：性能差。例如，有了像BN[17]这样的现代组件，VGG-16可以在ImageNet上达到72%以上的top-1精度，这似乎已经过时了。我们的结构参数重构方法受到ResNet的启发，它显式地构造一个快捷分支，将信息流建模为\(y = x + f(x)\)，并使用一个残差块来学习\(f\)。当 \(x\)与\(f(x)\)的维度不一样时，公式变为\(y=g(x)+f(x)\)，\(g(x)\)是一个\(1 \times 1\)的卷积。resnet成功的一个解释是，这种多分支架构使模型成为众多较浅模型的隐式集合[35]。特别地，对于n个块，模型可以解释为2n个模型的集合，因为每个块将流分支成两条路径。由于多分支拓扑在推理上有缺陷，但分支似乎有利于训练[35]，我们使用多个分支来对众多模型进行训练的集成。

​ 为了使大多数成员更浅或更简单，我们使用ResNet-like恒等式（仅当维度匹配时）和\(1×1\)分支，使得构建块训练时的信息流为

\[y=x+g(x)+f(x)
\]

我们简单地堆叠几个这样的区块来建构训练时间模型。(注意，这样信息流中的结构在每层都一样，运算的时候就更快了)

​ 从与[35]相同的角度来看，模型变成了一个由n个block生成的\(3^{n}\)个成员组成的集合。训练后等价地转化为\(y=h(x)\)，其中h由一个conv层实现，其参数通过训练后的一系列代数参数导出。

---

Top
 --- 
Bottom

4.3 推理时的模型参数重构

​ 这里我们将介绍把\(y=x+g(x)+f(x)\)结构转换为\(y=h(x)\)结构。需要注意的是每一个分支在合并(相加)之前都使用了BN层。

一般地，我们假设输入channel为\(C_{1}\)，输出通道为\(C_{2}\)，则\(3 \times 3\)的卷积核的权值矩阵为：

\[W^{(3)} \in \mathbb{R}^{C_{2} \times C_{1} \times 3 \times 3}
\]

对于\(1 \times 1\)的分支， \(1 \times 1\)的卷积核的权值矩阵为：

\[W^{(1)} \in \mathbb{R}^{C_{2} \times C_{1}}
\]

我们使用\(\boldsymbol{\mu}^{(3)}, \boldsymbol{\sigma}^{(3)},\boldsymbol{\gamma}^{(3)}, \boldsymbol{\beta}^{(3)}\)分别表示\(3 \times 3\)之后BN层的累计均值、标准差、缩放因子、偏置；

我们使用\(\boldsymbol{\mu}^{(1)}, \boldsymbol{\sigma}^{(1)},\boldsymbol{\gamma}^{(1)}, \boldsymbol{\beta}^{(1)}\)分别表示\(1 \times 1\)之后BN层的累计均值、标准差、缩放因子、偏置；

我们使用\(\boldsymbol{\mu}^{(0)}, \boldsymbol{\sigma}^{(0)},\boldsymbol{\gamma}^{(0)}, \boldsymbol{\beta}^{(0)}\)分别表示identity分支的累计均值、标准差、缩放因子、偏置；

令\(M^{(1)} \in \mathbb{R}^{N\times C_{1}\times H_{1}\times W_{1}}\)表示输入，\(M^{(2)} \in \mathbb{R}^{N\times C_{2}\times H_{2}\times W_{2}}\)表示输出。\(*\)表示卷积操作。

如果\(C_{1}=C_{2}, H_{1}=H_{2}, W_{1}=W_{2}\)，则有：

\[\begin{equation}
\begin{aligned}
M^{(2)} = BN(M^{(1)} * W^{(3)}, \boldsymbol{\mu}^{(3)}, \boldsymbol{\sigma}^{(3)},\boldsymbol{\gamma}^{(3)}, \boldsymbol{\beta}^{(3)})
+ BN(M^{(1)} * W^{(1)}, \boldsymbol{\mu}^{(1)}, \boldsymbol{\sigma}^{(1)},\boldsymbol{\gamma}^{(1)}, \boldsymbol{\beta}^{(1)})
+ BN(M^{(1)}, \boldsymbol{\mu}^{(0)}, \boldsymbol{\sigma}^{(0)},\boldsymbol{\gamma}^{(0)}, \boldsymbol{\beta}^{(0)})
\end{aligned}
\end{equation}
\]

否则，我们简单地不使用恒等映射分支，因此上面的方程只有前两项。对\(\forall 1\leq i\leq C_{2}\):

\[BN(M,\boldsymbol{\mu}, \boldsymbol{\sigma}, \boldsymbol{\gamma}, \boldsymbol{\beta})_{:,i,:,:}=(M_{:,i:,:}-\boldsymbol{\mu}_{i}) \frac{\boldsymbol{\gamma}_{i}}{\boldsymbol{\sigma}_{i}} + \boldsymbol{\beta}_{i}
\]

我们首先将每一个BN及其前一个conv层转换为带有偏置向量的conv。令\(\left \{{W}',{\boldsymbol{b}}' \right \}\)表示从\(\left \{W,\boldsymbol{\mu}, \boldsymbol{\sigma}, \boldsymbol{\gamma}, \boldsymbol{\beta} \right \}\)转换的kernel和bias，则有：

\[W_{i,:,:,:}^{'}=\frac{\boldsymbol{\gamma}_{i}}{\boldsymbol{\sigma}_{i}}W_{i,:,:,:}\quad, \quad{\boldsymbol{b}}'_{i}= \frac{\boldsymbol{-\boldsymbol{\mu}_{i}\gamma}_{i}}{\boldsymbol{\sigma}_{i}} + \boldsymbol{\beta}_{i}
\]

因此，容易验证对\(\forall 1\leq i\leq C_{2}\):

\[BN(M* W, \boldsymbol{\mu}, \boldsymbol{\sigma},\boldsymbol{\gamma}, \boldsymbol{\beta})_{:,i,:,:}=
(M*{W}')_{:,i,:,:} + {\boldsymbol{b}}'_{i}
\]

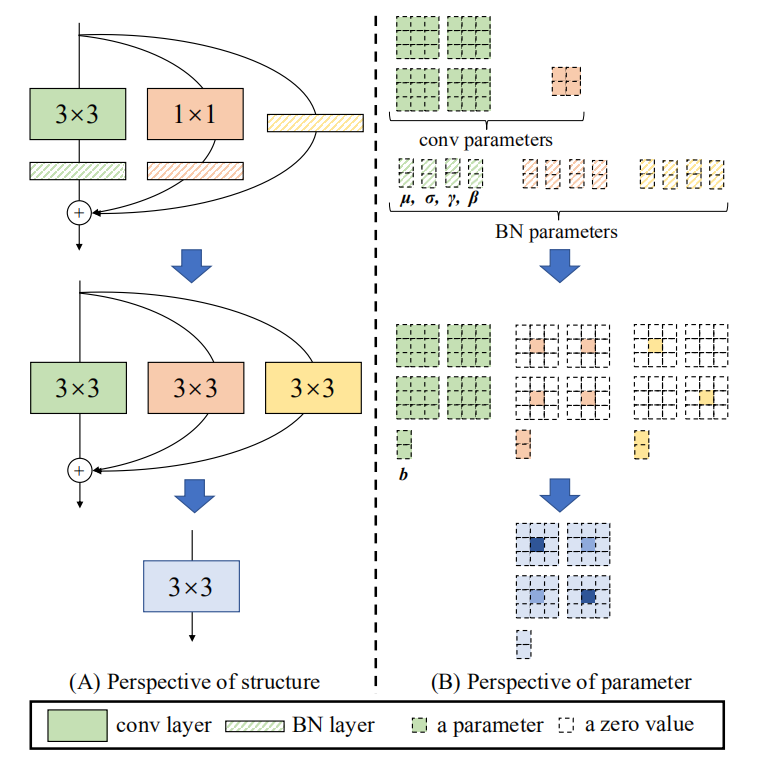
上述变换也适用于identity分支，因为identity 特征图可以看作是以单位矩阵为核的1×1变换。在这样的变换之后，我们将有一个3×3核、两个1×1核和三个偏置向量。然后我们将三个偏差向量相加得到最终偏差，将1×1的核加到3×3核的中心点得到最终的3×3核，这很容易实现，首先将两个1×1核置零到3×3，然后将三个核相加，如下图所示。注意，这种变换的等价性要求3×3和1×1层具有相同的步幅，并且后者的填充配置应比前者少一个像素。例如，对于将输入填充一个像素的3×3层（这是最常见的情况），1×1层的填充应为0。

---

Top
 --- 
Bottom

4.4 结构规格

​ 下表展示了RepVGG的规格，包括深度和宽度。RepVGG是VGG风格的平面网络，且大量使用\(3 \times 3\)的卷积，但是没有像VGG网络那样使用最大池化，因为设计这种网络只使用一种操作，可以加快运行速度。所有的stage都使用Repblock替换了\(3 \times 3\)的卷积，每层的第一个卷积操作，进行下采样。对于图像分类，使用全局平均池化接全连接层，作为head。对于其他任务，任务特定的头可以用所有层生成的特征。

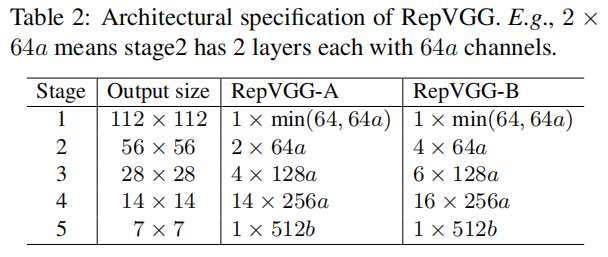
关于每个stage的layer数量，主要由如下的三个原则确定：

• 第一级的分辨率很高，非常耗时，因此我们只使用一层来降低延迟。
• 最后一级应该有更多的通道，所以我们只使用一层来保存参数。
• 我们将大多数层放在倒数第二个stage（在ImageNet上具有\(14 \times 14\)的输出分辨率），跟随ResNet及其最新变体。（如，ResNet-101使用了69个layer在\(14 \times 14\)的阶段）

最后，我们对5个stage的层数分配是：[1, 2, 4, 14, 1]，并命名为RepVGG-A。我们也构建了一个更深的RepVGG-B，在stage2、stage3、stage4都增加了2层。

​ RepVGG-A用于和其他轻量级的模型进行比较；RepVGG-B用于和ResNet-18/34/50这种中等体量的模型进行比较 。当然RepVGG-B取得了更好的性能表现。

​ 我们通过均匀缩放经典宽度设置[64、128、256、512]来确定层宽度。我们使用乘数a来缩放前四个阶段，b来缩放最后一个阶段，并且通常设置b>a，因为我们希望最后一层对于分类或其他下游任务具有更丰富的特征。由于RepVGG在最后一个阶段只有一个层，因此较大的b不会显著增加延迟或参数量。具体地 stage2、3、4、5的宽度分别为[64a、128a、256a、512b]。

​ 为了避免大特征图上的大卷积，如果\(a < 1\)，我们缩小stage1，但不放大它，因此stage1的宽度是\(min\left ( 64, 64a \right )\)。

​ 为了进一步减少参数和计算量，我们可以选择将分组的3×3 conv层与密集的conv层交错，以精度换取效率。具体来说，我们为RepVGG-A的第3、5、7、…、21层以及RepVGG-B的附加第23、25和27层设置groups数目为\(g\)。为了简单起见，我们将\(g\)全局设置为1、2或4，没有按层调整。我们不使用相邻的groupwise conv层，因为这将禁用通道间的信息交换并带来副作用：某个通道的输出只能从输入通道的一小部分中导出。注意，1×1分支应具有与3×3 conv相同的groups数目为\(g\)。

---

Top
 --- 
Bottom

完