牛客网多校第5场 F take 【思维+数学期望】

题目：戳这里

思路来源：视频讲解

题意：有n个箱子按1...n标号，每个箱子有大小为di的钻石概率为pi，我们初始有个大小为0的钻石，从1到n按顺序打开箱子，遇到比手中大的箱子就换，求交换次数的数学期望。

解题思路：这题跟上题[点这里]很像，都是找到一个子状态，利用数学期望的可加性，处理求和即可。这里的子状态为每一次交换的状态，即

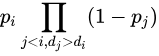
前j个比i大的概率积用树状数组维护。

附ac代码：

  1 #include <cstdio>
  2 #include <cstdlib>
  3 #include <iostream>
  4 #include <cstring>
  5 #include <algorithm>
  6 #include <cmath>
  7 #include <queue>
  8 #include <vector>
  9 #include <string>
 10 #include <map>
 11 #include <set>
 12 using namespace std;
 13 typedef long long ll;
 14 const ll mod = 998244353;
 15 const int maxn = 1e5 + 10;
 16 int n;
 17 struct nod
 18 {
 19     int id;
 20     ll d;
 21     ll p;
 22 }bx[maxn];
 23 bool cmp(nod a, nod b)
 24 {
 25     if(a.d > b.d)   return 1;
 26     else if(a.d == b.d && a.id < b.id) return 1;
 27     return 0;
 28 }
 29 ll pmul(ll a, ll b)
 30 {
 31     ll res = 0;
 32     while(b)
 33     {
 34         if(b&1)
 35             res = (res + a) % mod;
 36         b >>= 1;
 37         a = (a + a) % mod;
 38     }
 39     return res;
 40 }
 41 ll pmod(ll a, ll b)
 42 {
 43     ll res = 1;
 44     while(b)
 45     {
 46         if(b&1)
 47             res = pmul(res, a) % mod;
 48         b >>= 1;
 49         a = pmul(a, a) % mod;
 50     }
 51     return res;
 52 }
 53 ll exgcd(ll a, ll b, ll &x, ll &y)
 54 {
 55     if(a == 0 && b == 0) return -1;
 56     if(b == 0)
 57     {
 58         x = 1;y = 0;
 59         return a;
 60     }
 61     ll d = exgcd(b, a % b, y, x);
 62     y -= a/b*x;
 63     return d;
 64 }
 65 ll mod_rev(ll a, ll n)
 66 {
 67     ll x, y;
 68     ll d = exgcd(a, n, x, y);
 69     if(d == 1) return (x % n + n) % n;
 70     else return -1;
 71 }
 72 int lowbit(int x)
 73 {
 74     return x&(-x);
 75 }
 76 ll c[maxn * 4];
 77 ll getm(int i)
 78 {
 79     ll s = 1;
 80     while(i > 0)
 81     {
 82         s = pmul(s , c[i]) % mod;
 83         i -= lowbit(i);
 84     }
 85     return s;
 86 }
 87 void add(int i, ll val)
 88 {
 89     while(i <= n)
 90     {
 91         c[i] = pmul(c[i], val) %mod;
 92         i += lowbit(i);
 93     }
 94 }
 95 int main()
 96 {
 97
 98     ll inv = mod_rev(100ll, mod);
 99   //  printf("%lld\n", inv);
100     scanf("%d", &n);
101     for(int i = 0; i < maxn; ++i)
102         c[i] = 1;
103     for(int i = 1; i <= n; ++i)
104     {
105         scanf("%lld %lld", &bx[i].p, &bx[i].d);
106         bx[i].id = i;
107     }
108     sort(bx + 1, bx + 1 + n, cmp);
109
110     ll ans = 0;
111     for(int i = 1; i <= n; ++i)
112     {
113        // printf("%lld\n", getm(bx[i].id));
114         //printf("%lld %lld %d\n", bx[i].p, bx[i].d, bx[i].id);
115         ans = (ans + getm(bx[i].id) * bx[i].p % mod * inv % mod) % mod;
116         add(bx[i].id, ((100 - bx[i].p) * inv) % mod);
117     }
118     printf("%lld\n", ans);
119 }