树状数组 && 板子

本文树状数组讲解转载于：https://www.cnblogs.com/xenny/p/9739600.html

本文新加内容为模板代码部分

1.什么是树状数组？

顾名思义，就是用数组来模拟树形结构呗。那么衍生出一个问题，为什么不直接建树？答案是没必要，因为树状数组能处理的问题就没必要建树。和Trie树的构造方式有类似之处。

2.树状数组可以解决什么问题

可以解决大部分基于区间上的更新以及求和问题。

3.树状数组和线段树的区别在哪里

树状数组可以解决的问题都可以用线段树解决，这两者的区别在哪里呢？树状数组的系数要少很多，就比如字符串模拟大数可以解决大数问题，也可以解决1+1的问题，但没人会在1+1的问题上用大数模拟。

4.树状数组的优点和缺点

修改和查询的复杂度都是O(logN)，而且相比线段树系数要少很多，比传统数组要快，而且容易写。

缺点是遇到复杂的区间问题还是不能解决，功能还是有限。

5.树状数组的时间复杂度

树状数组建树时间复杂度为O(N）

树状数组查询和修改时间复杂度为O(logN)

一、树状数组介绍

二叉树大家一定都知道，如下图

如果每个父亲都存的是两个儿子的值，是不是就可以解决这类区间问题了呢。是的没错，但是这样的树形结构，叫做线段树。

那真的的树形结构是怎样的，和上图类似，但省去了一些节点，以达到用数组建树。

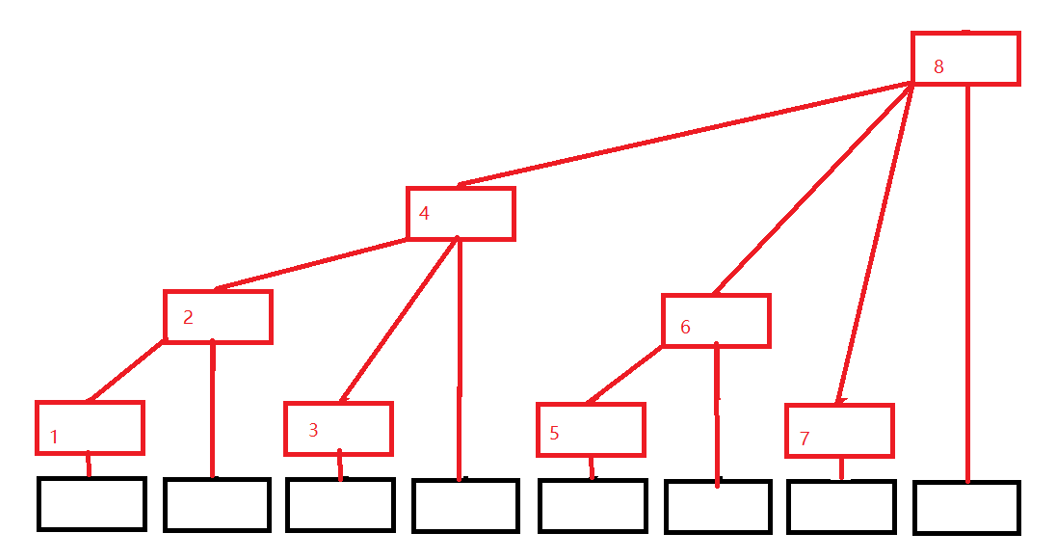
黑色数组代表原来的数组（下面用A[i]代替），红色结构代表我们的树状数组(下面用C[i]代替)，发现没有，每个位置只有一个方框，令每个位置存的就是子节点的值的和，则有

• C[1] = A[1];
• C[2] = A[1] + A[2];
• C[3] = A[3];
• C[4] = A[1] + A[2] + A[3] + A[4];
• C[5] = A[5];
• C[6] = A[5] + A[6];
• C[7] = A[7];
• C[8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8];

可以发现，这颗树是有规律的

C[i] = A[i - 2^k+1] + A[i - 2^k+2] + ... + A[i];   //k为i的二进制中从最低位到高位连续零的长度，get_sum函数原理就是这个

例如i = 8(1000)时候，k = 3，可自行验证。

这个怎么实现求和呢，比如我们要找前7项和，那么应该是SUM = C[7] + C[6] + C[4];

而根据上面的式子，容易的出SUM_i = C[i] + C[i-2^k1] + C[(i - 2^k1) - 2^k2] + .....；(SUM_i表示区间[1,i]内所有数之和) 

　　　　　　　　　　　　　这里的k1为i的“二进制中从最低位到高位连续零”，k2为（i-2^k1）的“二进制中从最低位到高位连续零”，之后的也是这样

其实树状数组就是一个二进制上面的应用。

现在新的问题来了2^k（单独对一个i求2^k）该怎么求呢，不难得出2^k = i&(i^(i-1));但这个还是不好求出呀，前辈的智慧就出来了，2^k = i&(-i);

为什么呢？

这里利用的负数的存储特性，负数是以补码存储的，对于整数运算 x&(-x)有

       ● 当x为0时，即 0 & 0，结果为0；

       ●当x为奇数时，最后一个比特位为1，取反加1没有进位，故x和-x除最后一位外前面的位正好相反，按位与结果为0。结果为1。

       ●当x为偶数，且为2的m次方时，x的二进制表示中只有一位是1（从右往左的第m+1位），其右边有m位0，故x取反加1后，从右到左第有m个0，第m+1位及其左边全是1。这样，x& (-x) 得到的就是x。 

       ●当x为偶数，却不为2的m次方的形式时，可以写作x= y * (2^k)。其中，y的最低位为1。实际上就是把x用一个奇数左移k位来表示。这时，x的二进制表示最右边有k个0，从右往左第k+1位为1。当对x取反时，最右边的k位0变成1，第k+1位变为0；再加1，最右边的k位就又变成了0，第k+1位因为进位的关系变成了1。左边的位因为没有进位，正好和x原来对应的位上的值相反。二者按位与，得到：第k+1位上为1，左边右边都为0。结果为2^k。

        总结一下：x&(-x)，当x为0时结果为0；x为奇数时，结果为1；x为偶数时，结果为x中2的最大次方的因子。

而且这个有一个专门的称呼，叫做lowbit，即取2^k。

二、模板代码

1、建立树状数组、修改某位置点的大小、询问区间内所有数之和

上面已经解释了如何用树状数组求区间和，那么如果我们要更新某一个点的值呢，还是一样的，上面说了C[i] = A[i - 2^k+1] + A[i - 2^k+2] + ... + A[i]，那么如果我们更新某个A[i]的值，则会影响到所有包含有A[i]位置。如果求A[i]包含哪些位置里呢，同理有

A[i] 包含于 C[i + 2^k]、C[(i + 2^k) + 2^k]...；  //update函数的原理就是这个

模板例题：hdu 1166

代码：

 1 #include<stdio.h>
 2 #include<iostream>
 3 #include<algorithm>
 4 #include<string.h>
 5 using namespace std;
 6 const int maxn=5e5+10;
 7 int v,tree[maxn];
 8 int n;
 9 int lowbit(int x)
10 {
11     return x&(-x);
12 }
13 void update(int i,int x)
14 {
15     while(i<=n)
16     {
17         tree[i]+=x;
18         i+=lowbit(i);
19     }
20 }
21 int get_sum(int i)  //获取区间[1,i]所有数之和
22 {
23     int ans=0;
24     while(i>0)
25     {
26         ans+=tree[i];
27         i-=lowbit(i);
28     }
29     return ans;
30 }
31 int main()
32 {
33     int t,p=0;
34     scanf("%d",&t);
35     while(t--)
36     {
37         memset(tree,0,sizeof(tree));
38         scanf("%d",&n);
39         for(int i=1;i<=n;++i)
40         {
41             scanf("%d",&v);
42             update(i,v);
43         }
44         char s[20];
45         int  x,y;
46         printf("Case %d:\n",++p);
47         while(~scanf("%s",s))
48         {
49             if(s[0]=='E') break;
50             else if(s[0]=='Q')
51             {
52                 scanf("%d%d",&x,&y);
53                 printf("%d\n",get_sum(y)-get_sum(x-1));
54             }
55             else if(s[0]=='A')
56             {
57                 scanf("%d%d",&x,&y);
58                 update(x,y);
59             }
60             else if(s[0]=='S')
61             {
62                 scanf("%d%d",&x,&y);
63                 update(x,-y);
64             }
65         }
66     }
67     return 0;
68 }

2、建立树状数组、区间更新、单点查询：

如果题目是让你把x-y区间内的所有值全部加上k或者减去k，然后查询操作是问某个点的值，这种时候该怎么做呢。如果是像上面的树状数组来说，就必须把x-y区间内每个值都更新，这样的复杂度肯定是不行的，这个时候，就不能再用数据的值建树了，这里我们引入差分，利用差分建树。

假设我们规定A[0] = 0;

则有 A[i] = Σⁱ_{j = 1}D[j];(D[j] = A[j] - A[j-1])，即前面i项的差值和，这个有什么用呢？例如对于下面这个数组

• A[] = 1 2 3 5 6 9
• D[] = 1 1 1 2 1 3

如果我们把[2,5]区间内值加上2，则变成了

• A[] = 1 4 5 7 8 9
• D[] = 1 3 1 2 1 1

发现了没有，当某个区间[x,y]值改变了，区间内的差值是不变的，只有D[x]和D[y+1]的值发生改变，至于为什么我想我就不用解释了吧。

所以我们就可以利用这个性质对D[]数组建立树状数组。

例题：P3368 【模板】树状数组 2

代码：

 1 #include<stdio.h>
 2 #include<string.h>
 3 #include<iostream>
 4 #include<algorithm>
 5 using namespace std;
 6 const int maxn=5e5+10;
 7 int n,m,tree[maxn];
 8 int lowbit(int x)
 9 {
10     return x&(-x);
11 }
12 void update(int x,int y)
13 {
14     while(x<=n)
15     {
16         tree[x]+=y;
17         x+=lowbit(x);
18     }
19 }
20 int get_sum(int x)
21 {
22     int ans=0;
23     while(x>0)
24     {
25         ans+=tree[x];
26         x-=lowbit(x);
27     }
28     return ans;
29 }
30 int main()
31 {
32     while(~scanf("%d%d",&n,&m))
33     {
34         memset(tree,0,sizeof(tree));
35         int start,now;
36         scanf("%d",&start);
37         update(1,start);
38         for(int i=2; i<=n; ++i)
39         {
40             scanf("%d",&now);
41             update(i,now-start);
42             start=now;
43         }
44         while(m--)
45         {
46             int x,y,z;
47             scanf("%d",&x);
48             if(x==1)
49             {
50                 scanf("%d%d%d",&x,&y,&z);
51                 update(x,z);
52                 update(y+1,-z);
53             }
54             else
55             {
56                 scanf("%d",&x);
57                 printf("%d\n",get_sum(x));
58             }
59         }
60
61     }
62     return 0;
63 }

3、建立树状数组、区间修改、区间查询

上面我们说的差值建树状数组，得到的是某个点的值，那如果我既要区间更新，又要区间查询怎么办。这里我们还是利用差分，由上面可知

∑ⁿ_{i = 1}A[i] = ∑ⁿ_{i = 1} ∑ⁱ_{j = 1}D[j];

则A[1]+A[2]+...+A[n]

= (D[1]) + (D[1]+D[2]) + ... + (D[1]+D[2]+...+D[n])

= n*D[1] + (n-1)*D[2] +... +D[n]

= n * (D[1]+D[2]+...+D[n]) - (0*D[1]+1*D[2]+...+(n-1)*D[n])

所以上式可以变为∑ⁿ_{i = 1}A[i] = n*∑ⁿ_{i = 1}D[i] -  ∑ⁿ_{i = 1}( D[i]*(i-1) );

如果你理解前面的都比较轻松的话，这里也就知道要干嘛了，维护两个数状数组，sum1[i] = D[i]，sum2[i] = D[i]*(i-1);

例题：A Simple Problem with Integers

代码：

 1 #include<stdio.h>
 2 #include<string.h>
 3 #include<iostream>
 4 #include<algorithm>
 5 using namespace std;
 6 const int maxn=1e5+10;
 7 typedef long long ll;
 8 ll n,m,tree[maxn],tree2[maxn];
 9 ll lowbit(ll x)
10 {
11     return x&(-x);
12 }
13 void update(ll x,ll y)
14 {
15     ll i=x-1;
16     while(x<=n)
17     {
18         tree[x]+=y;
19         tree2[x]+=i*y;
20         x+=lowbit(x);
21     }
22 }
23 ll get_sum(ll x)
24 {
25     ll ans=0;
26     ll i=x;
27     while(x>0)
28     {
29         ans=ans+i*tree[x]-tree2[x];
30         x-=lowbit(x);
31     }
32     return ans;
33 }
34 int main()
35 {
36     while(~scanf("%lld%lld",&n,&m))
37     {
38         memset(tree,0,sizeof(tree));
39         memset(tree2,0,sizeof(tree2));
40         ll start,now;
41         scanf("%lld",&start);
42         update(1,start);
43         for(ll i=2; i<=n; ++i)
44         {
45             scanf("%lld",&now);
46             update(i,now-start);
47             start=now;
48         }
49         while(m--)
50         {
51             char s[5];
52             ll x,y,z;
53             scanf("%s",s);
54             if(s[0]=='C')
55             {
56                 scanf("%lld%lld%lld",&x,&y,&z);
57                 update(x,z);
58                 update(y+1,-z);
59             }
60             else
61             {
62                 scanf("%lld%lld",&x,&y);
63                 printf("%lld\n",get_sum(y)-get_sum(x-1));
64             }
65         }
66     }
67     return 0;
68 }