7.9 NOI模拟赛 C.走路 背包 dp 特异性

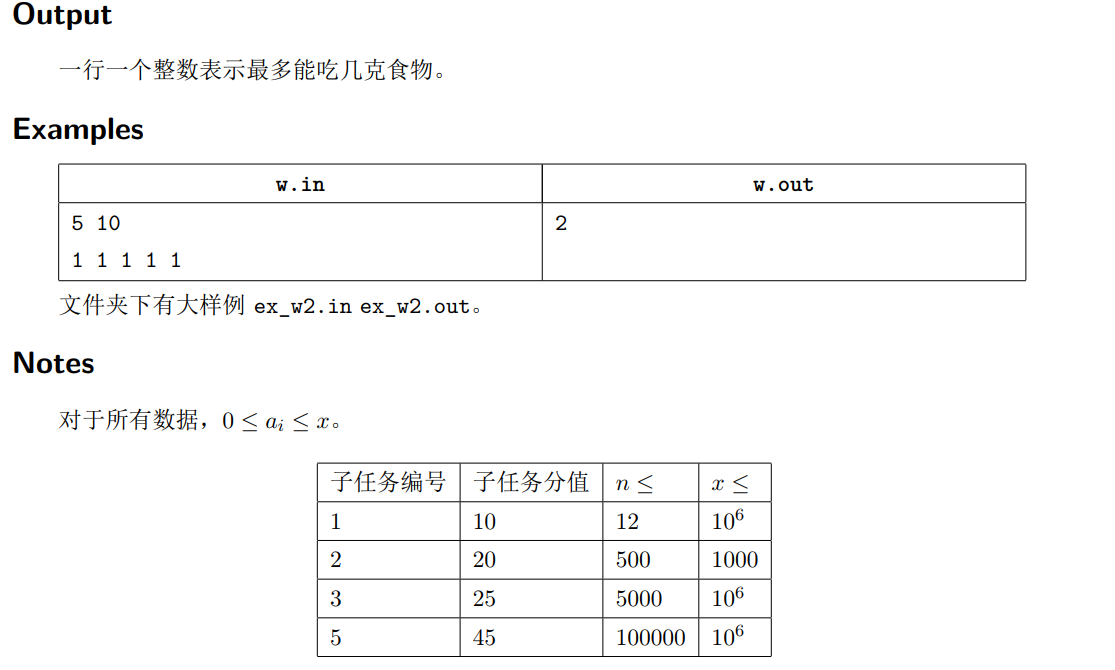
(啊啊啊 什么考试的时候突然降智这题目硬生生没想出来。

容易发现是先走到某个地方 然后再走回来的 然后在倒着走的路径上选择一些点使得最后的得到的最多。

设\(f_{i,j}\)表示到达i这个点选择的价值为j的最大获得的值 这显然是一个01背包。

然后不断更新答案即可。可以直接从前往后坐。复杂度\(n\cdot m\)

code

//#include<bits\stdc++.h>
#include<iostream>
#include<iomanip>
#include<cstdio>
#include<cstring>
#include<string>
#include<ctime>
#include<cmath>
#include<cctype>
#include<cstdlib>
#include<queue>
#include<deque>
#include<stack>
#include<vector>
#include<algorithm>
#include<utility>
#include<bitset>
#include<set>
#include<map>
#define ll long long
#define db double
#define INF 10000000000000010ll
#define ldb long double
#define pb push_back
#define put_(x) printf("%d ",x);
#define get(x) x=read()
#define gt(x) scanf("%d",&x)
#define gi(x) scanf("%lf",&x)
#define put(x) printf("%d\n",x)
#define putl(x) printf("%lld\n",x)
#define gc(a) scanf("%s",a+1)
#define rep(p,n,i) for(RE int i=p;i<=n;++i)
#define go(x) for(int i=lin[x],tn=ver[i];i;tn=ver[i=nex[i]])
#define fep(n,p,i) for(RE int i=n;i>=p;--i)
#define vep(p,n,i) for(RE int i=p;i<n;++i)
#define pii pair<int,int>
#define mk make_pair
#define RE register
#define P 1000000007
#define gf(x) scanf("%lf",&x)
#define pf(x) ((x)*(x))
#define uint unsigned long long
#define ui unsigned
#define EPS 1e-8
#define sq sqrt
#define S second
#define F first
#define mod 998244353
using namespace std;
char buf[1<<15],*fs,*ft;
inline char getc()
{
    return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline int read()
{
    RE int x=0,f=1;RE char ch=getc();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();}
    while(ch>='0'&&ch<='9'){x=((ll)x*10+ch-'0')%mod;ch=getc();}
    return x*f;
}
const int MAXN=1000010,maxn=100010;
int n,m,ans;
int f[MAXN];
int a[MAXN];
int main()
{
	freopen("w.in","r",stdin);
	freopen("w.out","w",stdout);
	get(n);get(m);
	rep(1,n,i)get(a[i]);
	rep(1,n,i)
	{
		fep(m-2*i,(ll)i*a[i],j)f[j]=max(f[j],f[j-i*a[i]]+a[i]);
		ans=max(ans,f[m-2*i]);
	}
	put(ans);
	return 0;
}

这样只有30分 发现这是一个标准的01背包 而众所周知 01背包的复杂度的下界就是$n\cdot m$所以是优化不了的。

上午我也止步于此 不断的挣扎却毫无思路。

其实主要是观察到 获得的值域是m的 这一点是和原本普通的01背包是有所不同的 这点特异性还是很容易发现的吧？

所以可以想到把状态翻转 \(f_i\)表示得到i所花费的最小代价。

考虑正着做不太爽 和上面复杂度一样 倒着做 就可以发现了 对于每个i 状态数量为\(\frac{m}{i}\)

所以就可以过了。我真的是太弱了。

code

//#include<bits\stdc++.h>
#include<iostream>
#include<iomanip>
#include<cstdio>
#include<cstring>
#include<string>
#include<ctime>
#include<cmath>
#include<cctype>
#include<cstdlib>
#include<queue>
#include<deque>
#include<stack>
#include<vector>
#include<algorithm>
#include<utility>
#include<bitset>
#include<set>
#include<map>
#define ll long long
#define db double
#define INF 1000000000
#define ldb long double
#define pb push_back
#define put_(x) printf("%d ",x);
#define get(x) x=read()
#define gt(x) scanf("%d",&x)
#define gi(x) scanf("%lf",&x)
#define put(x) printf("%d\n",x)
#define putl(x) printf("%lld\n",x)
#define gc(a) scanf("%s",a+1)
#define rep(p,n,i) for(RE int i=p;i<=n;++i)
#define go(x) for(int i=lin[x],tn=ver[i];i;tn=ver[i=nex[i]])
#define fep(n,p,i) for(RE int i=n;i>=p;--i)
#define vep(p,n,i) for(RE int i=p;i<n;++i)
#define pii pair<int,int>
#define mk make_pair
#define RE register
#define P 1000000007
#define gf(x) scanf("%lf",&x)
#define pf(x) ((x)*(x))
#define uint unsigned long long
#define ui unsigned
#define EPS 1e-8
#define sq sqrt
#define S second
#define F first
#define mod 998244353
using namespace std;
char buf[1<<15],*fs,*ft;
inline char getc()
{
    return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline int read()
{
    RE int x=0,f=1;RE char ch=getc();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();}
    while(ch>='0'&&ch<='9'){x=((ll)x*10+ch-'0')%mod;ch=getc();}
    return x*f;
}
const int MAXN=1000010,maxn=100010;
int n,m,ans;
ll f[MAXN];//f[i]表示拿了i的最小代价.
ll a[MAXN];
int main()
{
	freopen("w.in","r",stdin);
	freopen("w.out","w",stdout);
	gt(n);gt(m);
	rep(1,n,i)gt(a[i]);
	memset(f,0x3f,sizeof(f));f[0]=0;
	fep(n,1,i)
	{
		if(!a[i])continue;
		fep(m/i,a[i]+1,j)f[j]=min(f[j],f[j-a[i]]+a[i]*i);
		f[a[i]]=min(f[a[i]],a[i]*i+2*i);
	}
	fep(m,0,j)if(f[j]<=m){put(j);return 0;}
}

注意开long long.