【2019北京集训2】Elephant 平衡树

题目大意：给你一个长度为$n$的序列$A_i$，有$q$次操作，每次操作为以下三种之一：

询问区间的$F_M(A_i)$的最大公约数。

区间翻转，区间加一个正数。

我们定义$gcd(0,0)=0$，且$F_M(A_i)$为在一个$M$个点的无向完全图中从第一个点开始走$k$步后回到第一个点的方案数。

数据范围：$n,q≤10^5$，$0≤A_i≤10^8$，$2≤M≤10^9$。

我们先考虑下如何求$F_M(x)$。

经过打表（大雾），我们发现：

若$x$为偶数，则$F_M(x)=M\times(F_M(x-1)+1)$

若$x$为奇数，则$F_M(x)=M\times(F_M(x-1)-1)$

特别地，$F_M(0)=1$，$F_M(1)=0$

我们显然可以$O(2\times 10^8)$预处理或者直接矩阵快速幂计算。

继续打表，我们发现：$gcd(F_M(x-1),F_M(y-1))=F_M(gcd(x-1,y-1))$，感兴趣的同学可以证明一下（反正我不会）

我们发现，如果询问的区间中存在数字0，则这个区间的GCD显然为1

考虑到要资瓷区间翻转，区间查询0的个数，区间抹去0，对于这部分我们需要单独开一棵splay来维护。

考虑维护>1部分的数。

我们先不考虑翻转的情况。

我们将差分后的数列丢入一棵splay中，每个节点维护整棵子树内的权值和，还有子树内的GCD

我们需要查询区间$[l,r]$的$GCD$时，我们只需要查询$[l+1,r]$的区间GCD，然后再和第$l$个位置的值求GCD即可输出。

原因显然

考虑翻转区间$[l,r]$的情况：不难发现受到影响的区间为$[l,r+1]$。

然后，经过冷静分析（大雾），我们发现翻转前后有这样的性质：

1，第$l$个位置的查分值和第$r+1$个位置的差分值需要单独更新。

2，区间$[l+1,r]$内的差分值等于原区间$[l+1,r]$内的差分值翻转再取相反数。

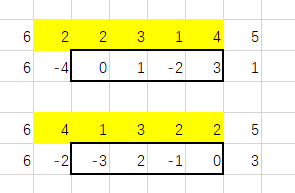
上面这张图是一个例子，证明显然。

然后，我们开几个标记打一下就可以了。

然后就没有然后了，注意细节

时间复杂度：$O(n\log^2\ n)$

 #include<bits/stdc++.h>
 #define M 200005
 #define MOD 323232323
 #define L long long
 #define lc(x) ch[(x)][0]
 #define rc(x) ch[(x)][1]
 using namespace std;

 int GCD(int x,int y){return __gcd(abs(x),abs(y));}

 struct mat{
     L a[][]; mat(){memset(a,,sizeof(a));}
     void danwei(){a[][]=a[][]=a[][]=;}
     friend mat operator *(mat a,mat b){
         mat c;
         for(int i=;i<;i++)
         for(int j=;j<;j++)
         for(int k=;k<;k++)
         c.a[i][j]=(c.a[i][j]+a.a[i][k]*b.a[k][j])%MOD;
         return c;
     }
     friend mat operator ^(mat x,int b){
         mat ans; ans.danwei();
         while(b){
             if(b&) ans=ans*x;
             x=x*x; b>>=;
         }
         return ans;
     }
 };
 L P;
 L getans(int n){
     if(n==) return ;
     mat a;
     a.a[][]=a.a[][]=;
     a.a[][]=P*P%MOD;
     a.a[][]=(P-+MOD)%MOD;
     a=a^(n-);
     L res=a.a[][]*P%MOD;
     if(n&) res=P*(res+)%MOD;
     return res;
 }

 namespace FF{
     int siz[M]={},ch[M][]={},sum[M]={},tagf[M]={},val[M]={},rev[M]={},fa[M]={},use=;

     int root=;
     void pushup(int x){
         siz[x]=siz[lc(x)]+siz[rc(x)]+;
         sum[x]=sum[lc(x)]+sum[rc(x)]+val[x];
     }
     void upd(int x){rev[x]^=; swap(lc(x),rc(x)); }
     void cls(int x){tagf[x]=; sum[x]=val[x]=;}
     void pushdown(int x){
         if(rev[x]) upd(lc(x)),upd(rc(x)); rev[x]=;
         if(tagf[x]) cls(lc(x)),cls(rc(x)); tagf[x]=;
     }
     void rotate(int x,int &k){
         int y=fa[x],z=fa[y],l,r;
         l=(ch[y][]!=x); r=l^;
         if(y==k) k=x;
         else{
             if(lc(z)==y) ch[z][]=x;
             else ch[z][]=x;
         }
         fa[y]=x; fa[x]=z; fa[ch[x][r]]=y;
         ch[y][l]=ch[x][r]; ch[x][r]=y;
         pushup(y); pushup(x);
     }
     void pud(int x,int k){if(x!=k) pud(fa[x],k); pushdown(x);}

     void splay(int x,int &k){
         pud(x,k);
         while(x!=k){
             int y=fa[x],z=fa[y];
             if(y!=k){
                 if((lc(y)==x)==(lc(z)==y)) rotate(y,k);
                 else rotate(x,k);
             }
             rotate(x,k);
         }
     }
     int insert(int x,int id,int zhi){
         pushdown(x);
         if(!x){x=++use; val[x]=zhi;}
         else{
             if(siz[lc(x)]+<=id) rc(x)=insert(rc(x),id-siz[lc(x)]-,zhi),fa[rc(x)]=x;
             else lc(x)=insert(lc(x),id,zhi),fa[lc(x)]=x;
         }
         pushup(x); return x;
     }
     int find(int x,int k){
         pushdown(x);
         if(siz[lc(x)]+==k) return x;
         if(siz[lc(x)]>=k) return find(lc(x),k);
         return find(rc(x),k-siz[lc(x)]-);
     }
     void ins(int x,int k){
         root=insert(root,k,x);
         splay(use,root);
     }

     int query(int x,int y){
         int X=find(root,x),Y=find(root,y+);
         splay(X,root); splay(Y,rc(root));
         return sum[lc(Y)];
     }
     void updata(int x,int y){
         int X=find(root,x),Y=find(root,y+);
         splay(X,root); splay(Y,rc(root));
         cls(lc(Y));
         pushup(Y);
         pushup(root);
     }
     void setrev(int x,int y){
         int X=find(root,x),Y=find(root,y+);
         splay(X,root); splay(Y,rc(root));
         upd(lc(Y));
     }
 }

 int siz[M]={},ch[M][]={},gcd[M]={},sum[M]={},val[M]={},rev[M]={},fa[M]={},use=;

 int root=;
 void pushup(int x){
     siz[x]=siz[lc(x)]+siz[rc(x)]+;
     sum[x]=sum[lc(x)]+sum[rc(x)]+val[x];
     gcd[x]=GCD(GCD(gcd[lc(x)],gcd[rc(x)]),val[x]);
 }
 void upd(int x){rev[x]^=; swap(lc(x),rc(x)); sum[x]=-sum[x]; val[x]=-val[x];}
 void pushdown(int x){if(rev[x]) upd(lc(x)),upd(rc(x)); rev[x]=;}
 void rotate(int x,int &k){
     int y=fa[x],z=fa[y],l,r;
     l=(ch[y][]!=x); r=l^;
     if(y==k) k=x;
     else{
         if(lc(z)==y) ch[z][]=x;
         else ch[z][]=x;
     }
     fa[y]=x; fa[x]=z; fa[ch[x][r]]=y;
     ch[y][l]=ch[x][r]; ch[x][r]=y;
     pushup(y); pushup(x);
 }
 void pud(int x){if(x!=root) pud(fa[x]); pushdown(x);}

 void splay(int x,int &k){
     pud(x);
     while(x!=k){
         int y=fa[x],z=fa[y];
         if(y!=k){
             if((lc(y)==x)==(lc(z)==y)) rotate(y,k);
             else rotate(x,k);
         }
         rotate(x,k);
     }
 }
 int insert(int x,int id,int zhi){
     pushdown(x);
     if(!x){x=++use; val[x]=zhi;}
     else{
         if(siz[lc(x)]+<=id) rc(x)=insert(rc(x),id-siz[lc(x)]-,zhi),fa[rc(x)]=x;
         else lc(x)=insert(lc(x),id,zhi),fa[lc(x)]=x;
     }
     pushup(x); return x;
 }
 int find(int x,int k){
     pushdown(x);
     if(siz[lc(x)]+==k) return x;
     if(siz[lc(x)]>=k) return find(lc(x),k);
     return find(rc(x),k-siz[lc(x)]-);
 }
 void ins(int x,int k){
     root=insert(root,k,x);
     splay(use,root);
 }
 void del(int k){
     int x=find(root,k); splay(x,root);
     int y=find(root,k+); lc(y)=lc(x);
     fa[lc(x)]=y; fa[rc(x)]=; root=rc(x);
     splay(y,root); 

 }

 int getval(int id){
     int x=find(root,id+);
     splay(x,root);
     return val[x]+sum[lc(x)];
 }
 int query(int x,int y){
     if(x>y) return ;
     int X=find(root,x),Y=find(root,y+);
     splay(X,root);
     splay(Y,rc(root));
     return gcd[lc(Y)];
 }
 void updata(int id,int delta){
     int x=find(root,id);
     splay(x,root);
     val[x]+=delta;
     pushup(x);
 }

 void setrev(int x,int y){
     int X=find(root,x),Y=find(root,y+);
     splay(X,root);
     splay(Y,rc(root));
     upd(lc(Y));
     pushup(lc(Y));
     splay(lc(Y),root);
 }

 void setval(int x,int V){
     int X=find(root,x+);
     splay(X,root);
     val[X]=V;
     pushup(X);
 }

 int n,m,a[M]={};

 int main(){
     ins(,); ins(,);
     FF::ins(,); FF::ins(,);
     int cas; scanf("%d",&cas);
     scanf("%d%d%d",&P,&n,&m); P--;
     for(int i=;i<=n;i++) scanf("%d",a+i),a[i]--;

     for(int i=;i<=n+;i++){
         ins(a[i]-a[i-],i);
         FF::ins(a[i]==-,i);
     }

     while(m--){
         int op,x,y;
         scanf("%d%d%d",&op,&x,&y);
         if(op==){
             int F=FF::query(x,y);
             if(F) {printf("1\n"); continue;}
             int ans=query(x+,y);
             int las=getval(x);
             printf("%lld\n",getans(GCD(las,ans)));
         }
         if(op==){
             int k; scanf("%d",&k);
             updata(x+,k);
             updata(y+,-k);
             FF::updata(x,y);
         }
         if(op==){
             if(x==y) continue;
             int Vl=getval(x-);
             int VR=getval(y);
             int Vr=getval(y+);
             setrev(x+,y);
             FF::setrev(x,y);
             setval(x,VR-Vl);

             VR=getval(y);

             setval(y+,Vr-VR);
         }
     }
 }