Appium+python自动化1-环境搭建（上）

前言

appium可以说是做app最火的一个自动化框架，它的主要优势是支持android和ios，另外脚本语言也是支持java和Python。小编擅长Python，所以接下来的教程是appium+python的实例。

学习appium最大的难处在于环境的安装，80%的人死于环境安装，然后就没然后了，10%的人被环境折腾一周以上，只有剩下的10%人品好，可以顺利安装。

一、环境准备

小编的环境是Windows 7版本 64位系统（32位的同学自己想办法哦）

1.jdk1.6.0 （64位）

2.android-sdk_r24.3.4-windows

3.python:2.7（3.6也可以）

4.appium：1.4.13.1

5.Node.js：node-v4.4.7-x64

6.Appium-Python-Client

二、jdk安装

1.下载jdk包，小编的是64位1.6版本，其它高级版本应该也是可以的。根据自己的系统选择对应版本

2.一路傻瓜式安装，注意安装路径不要有空格，不要有中文。jdk和jre不要放在一个文件夹下

3.设置三个环境变量,我的电脑>选择“属性”->“高级”->“环境变量”->“系统变量”->“新建”

JAVA_HOME----D:\Java\jdk1.6.0” （根据自己安装路径填写）

1471426392934219.png746x404 18.4 KB

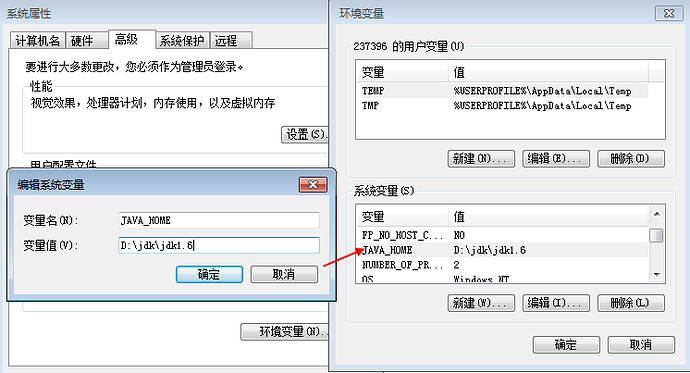
CLASSPATH--- .;%JAVA_HOME%\lib;%JAVA_HOME%\lib\tools.jar;

1471426406862959.png783x404 19.6 KB

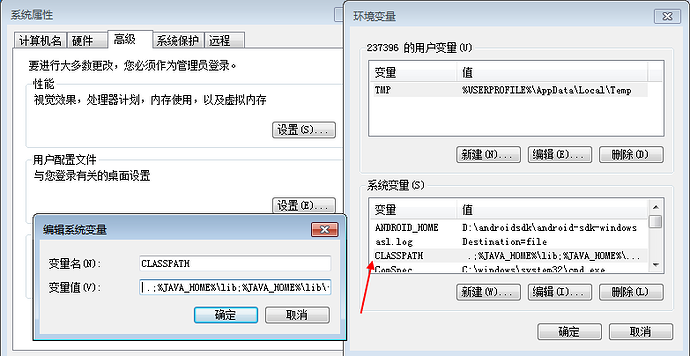
PATH-----;%JAVA_HOME%\bin;%JAVA_HOME%\jre\bin;

在path路径下加上面那两个，这里就不多说了

4.打开cmd验证是否安装成功，输入java -version，然后输入javac

能显示版本号和下面的帮助信息说明安装成功

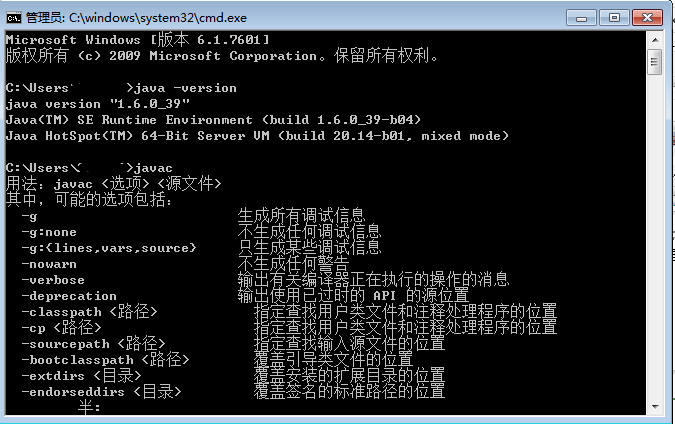
三、android-sdk下载安装

1.下载android-sdk,这个是做android测试和开发的必备环境，如果不会下载的话，在QQ群：512200893群文件下载

2.解压后，里面有个SDK manager.exe双击打开

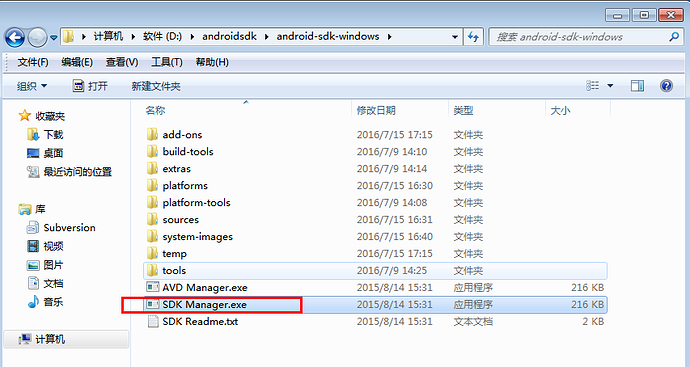
3.勾选你要下载的API版本和对应的android版本，后面模拟器会用到（不下载用其它模拟器也行，或者真机），然后坐等下载

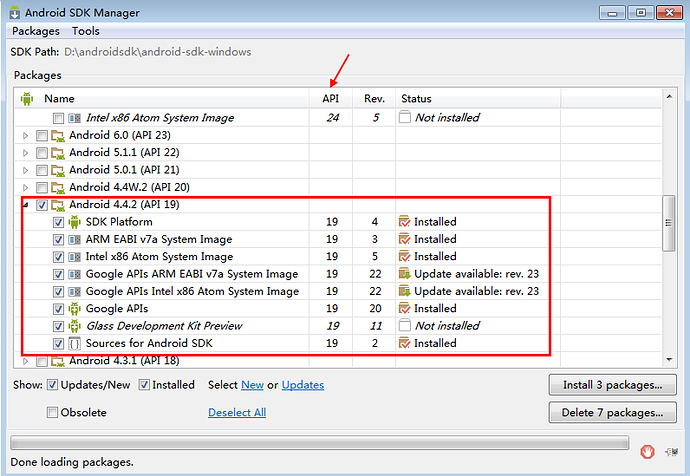
四、android-sdk环境变量

1.在系统变量新建：ANDROID_HOME，对应变量值为：D:\androidsdk\android-sdk-windows（sdk安装路径）

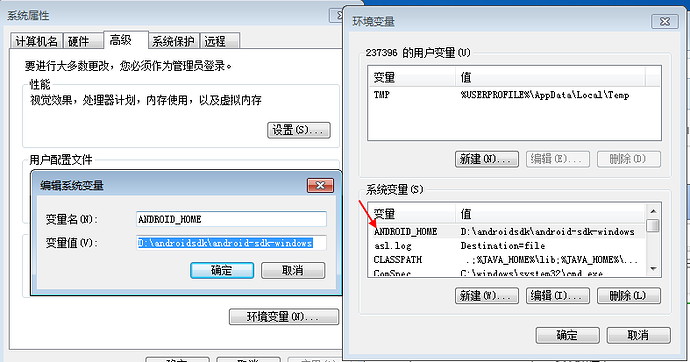
2.path添加两个变量，将以下箭头所指的两个文件路径添加到path里

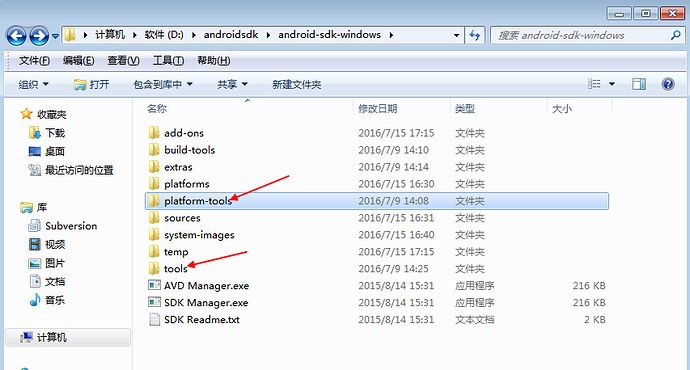
3.path里面添加D:\androidsdk\android-sdk-windows\tools和D:\androidsdk\android-sdk-windows\platform-tools

五、adb环境

1.因为adb是在D:\androidsdk\android-sdk-windows\platform-tools这个目录下的，所以上面添加了环境变量后，可以直接在cmd里面运行了。

2.在cmd输入adb可以查看对应版本号

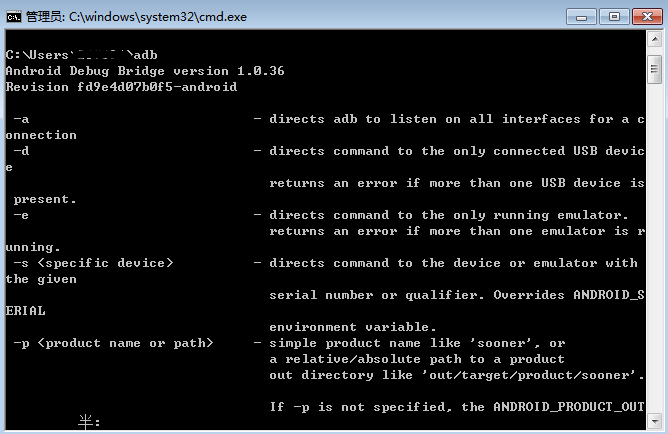
六、连接手机

1.手机用数据线连电脑，如果安装了91助手或者360什么的可以先下载手机驱动，确认手机能连上

2.打开cmd输入：adb devices,当屏幕上出现一串字符，后面显示devices说明连接成功（出现其它的提示，得检查自己的环境了）

到这里android的测试开发环境已经装好了，下一篇会教搭建搭建appium环境。安装过程中遇到各种奇葩问题，请卸载完后，仔细阅读，从第一行开始，一步一步走下来，中间任何一个环境出问题，都会导致最后appium运行失败。

在学习过程中有遇到疑问的，可以加appium（python+java） QQ群交流:330467341