使用.NET Core与Google Optimization Tools实现加工车间任务规划

前一篇文章《使用.NET Core与Google Optimization Tools实现员工排班计划Scheduling》算是一种针对内容的规划，而针对时间顺序任务规划，加工车间的工活儿是一个典型的场景。在加工车间有不同的工活儿，一般称为作业，每种作业都有多道工序，每道工序只能在特定的机器上完成。工序有不同的时长，而且是不能更改先后的。这些作业正是制造车间大规模生产线的任务，比如汽车零件制造。问题就是，工厂需要做一个最优的规划，使得作业严格按工序进行的前提下，消耗的时间最短，这样就保证了生产效率是最佳的。如果想做到最优规划，以下约束必不可少：

1. 在作业中必须要前一道工序完成才能进行下一道工序。

2. 对于一台机器，一次只能支持一个作业中的一道工序的运转。

3. 对于每道工序，一旦开始就必须完整地结束。

案例背景

---

以下是某个车间的作业情况，job代表作业，（m,p）代表了工序，其中m表示从0开始的机器编号，p代表了这道工序需要消耗的时长。本文假设了一个作业计划：

job 0 =  [(0, 3), (1, 2), (2, 2)]

job 1 =  [(0, 2), (2, 1), (1, 4)]

job 2 =  [(1, 4), (2, 3)]

如上所示，job 0有三道工序，第一道工序在0号机器用掉3个单位时长，第二道在1号机器用掉2个单位时长，第三道在2号机器用掉2个单位时长，以此类推，总共八道工序。

解决方案

---

有一种解决方案如下图，在一个时间轴上，每道工序有一个开始时间，占据一定的时长代表消耗部分，互相不会重叠，所有工序安置完毕，最长的地方就是整个作业全部完成的时长。

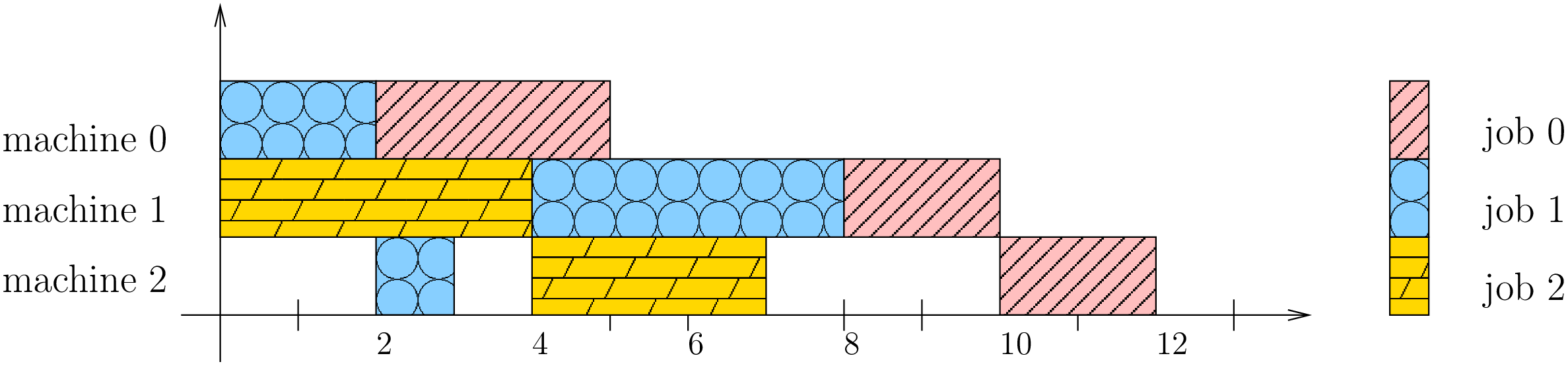
上图给了一个示范，一共消耗12个单位时长，当然这也不是最优的，后面通过编码我们再计算出最优的结果。

定义约束

---

首先我们将工序时长定义为task(i, j)，表示job i的第j道工序，定义t_i, j表示task(i, j)开始的时间点。有了这两种定义，按照之间的要求，于是有了如下的关系约束：

1. 连接约束，对于同一个作业，前一道工序加上消耗的时长就是后一道工序。比如，对于作业job 0来说，t_0, 2表示第二道工序开始的位置，最多消耗2个单位时长之后，就是第三道工序的位置，即：t_0, 2   + 2  ≤  t_0, 3。

2. 非连接约束，对于不同的作业，要保证前一道工序完成后才能进行下一道工序。比如在1号的机器上有task(0, 2)和task(2, 1)，它们消耗的时长分别是2和4个单位，那么就有：

t_0, 2   + 2  ≤  t_2, 1     如果task(0, 2)在task(2, 1)前运行的话

或者

t_2, 1   + 4  ≤  t_0, 2      如果task(2, 1)在task(0, 2)前运行的话

基于这个关系，前面案例的作业计划的约束关系如图所示：

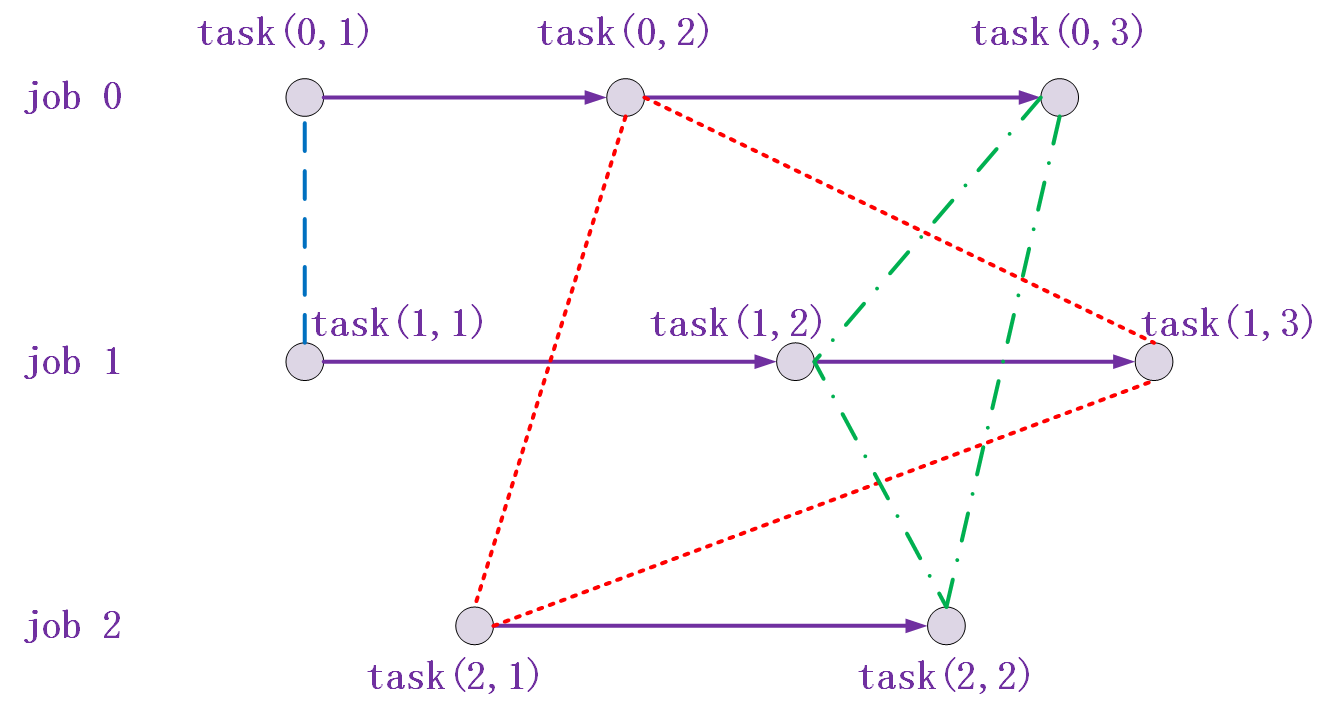
带箭头的实线表示了每个作业的工序，有连接约束的情况，而虚线表示了非连接约束的情况，实线有箭头是因为每个作业的工序是确定的，而虚线没有箭头也就说明顺序是没有确定的，这也正是我们要通过规划解决的问题。

最终求解目标

---

如果假定p_i, j表示task(i, j)的消耗时长，那么我们要解决的全局问题就是在所有task都完成后，求一个max_i, j  t_i, j +  p_i, j的最小值，表示生产效率最优的结果。

代码分解

---

看过本文开头谈到的前一篇文章后，对于项目初始化和相同的基本概念就不再介绍了。

首先定义一些初始化用的值。

// 创建约束求解器.
var solver = new Solver("jobshop");
var machines_count = ;
var jobs_count = ;
var all_machines = Enumerable.Range(, machines_count);
var all_jobs = Enumerable.Range(, jobs_count);

再定义出所有的工序。MakeFixedDurationIntervalVar就是OR-Tools专门用来创建间隔时间的变量类型。

// 将任务拆分成对应的机器和用时的结构
// job 0 = [(0, 3), (1, 2), (2, 2)]
// job 1 = [(0, 2), (2, 1), (1, 4)]
// job 2 = [(1, 4), (2, 3)]
var machines = new int[][]
{
    new[] { , ,  },
    new[] { , ,  },
    new[] { ,  }
};
 
var processing_times = new int[][]
{
    new[] { , ,  },
    new[] {, ,  },
    new[] { ,  }
};
 
// 计算总用时
var horizon = ;
foreach (var i in all_jobs)
    horizon += processing_times[i].Sum();
 
// 创建工序变量
var all_tasks = new Dictionary<(int, int), IntervalVar>();
foreach (var i in all_jobs)
{
    foreach (var j in Enumerable.Range(, machines[i].Length))
    {
        all_tasks[(i, j)] = solver.MakeFixedDurationIntervalVar(,
                                                    horizon,
                                                    processing_times[i][j],
                                                    false,
                                                    $"Job_{i}_{j}");
    }
}

然后定义连接约束和非连接约束，MakeDisjunctiveConstraints专门用来创建非连接约束的，StartsAfterEnd专门用来创建连接约束。

// 创建连接的顺序变量及连接关系
var all_sequences = new SequenceVarVector();
//var all_machines_jobs = new List<IntervalVar>();
foreach (var i in all_machines)
{
    var machines_jobs = new IntervalVarVector();
    foreach (var j in all_jobs)
    {
        foreach (var k in Enumerable.Range(, machines[j].Length))
        {
            if (machines[j][k] == i)
            {
                machines_jobs.Add(all_tasks[(j, k)]);
            }
        }
    }
    var disj = solver.MakeDisjunctiveConstraint(machines_jobs, $"machine {i}");
    all_sequences.Add(disj.SequenceVar());
    solver.Add(disj);
}
 
// 定义连接约束
foreach (var i in all_jobs)
{
    foreach (var j in Enumerable.Range(, machines[i].Length - ))
    {
        solver.Add(all_tasks[(i, j + )].StartsAfterEnd(all_tasks[(i, j)]));
    }
}

重点的部分，就是创建求解目标了。MakeMinimize用来求最小值，第二个参数表示每次移动的步长，直到有解为止。

// 创建求解的极值目标
var end_tasks = new IntVarVector();
foreach (var i in all_jobs)
{
    end_tasks.Add(all_tasks[(i, machines[i].Length - )].EndExpr().Var());
}
var obj_var = solver.MakeMax(end_tasks);
var objective_monitor = solver.MakeMinimize(obj_var.Var(), );
 
// 创建求解的对象
var sequence_phase = solver.MakePhase(all_sequences.ToArray(), Solver.SEQUENCE_DEFAULT);
var vars_phase = solver.MakePhase(new[] { obj_var.Var() }, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);
var main_phase = solver.Compose(new[] { sequence_phase, vars_phase });

最后是显示最优解结果的部分。

// 创建最后一个解决方案
var collector = solver.MakeLastSolutionCollector();
 
// 添加需要关注的变量
collector.Add(all_sequences.ToArray());
collector.AddObjective(obj_var.Var());
 
foreach (var i in all_machines)
{
    var sequence = all_sequences[i];
    var sequence_count = sequence.Size();
    for (var j = ; j < sequence_count; j++)
    {
        var t = sequence.Interval(j);
        collector.Add(t.StartExpr().Var());
        collector.Add(t.EndExpr().Var());
    }
}
 
// 显示结果
var disp_col_width = ;
if (solver.Solve(main_phase, new SearchMonitor[] { objective_monitor, collector }))
{
    Console.WriteLine("\nOptimal Schedule Length: {0}\n", collector.ObjectiveValue());
    var sol_line = "";
    var sol_line_tasks = "";
    Console.WriteLine("Optimal Schedule\n");
 
    foreach (var i in all_machines)
    {
        var seq = all_sequences[i];
        sol_line += $"Machine {i}: ";
        sol_line_tasks += $"Machine {i}: ";
        var sequence = collector.ForwardSequence(, seq);
        var seq_size = sequence.Count;
 
        foreach (var j in Enumerable.Range(, seq_size))
        {
            var t = seq.Interval(sequence[j]);
            sol_line_tasks += t.Name().PadRight(disp_col_width, ' ');
        }
 
        foreach (var j in Enumerable.Range(, seq_size))
        {
            var t = seq.Interval(sequence[j]);
            var sol_tmp = $"[{collector.Value(0, t.StartExpr().Var())},{collector.Value(0, t.EndExpr().Var())}]";
            sol_line += sol_tmp.PadRight(disp_col_width, ' ');
        }
        sol_line += "\n";
        sol_line_tasks += "\n";
    }
    Console.WriteLine(sol_line_tasks);
    Console.WriteLine("Time Intervals for Tasks\n");
    Console.WriteLine(sol_line);
}

运行后结果如下：

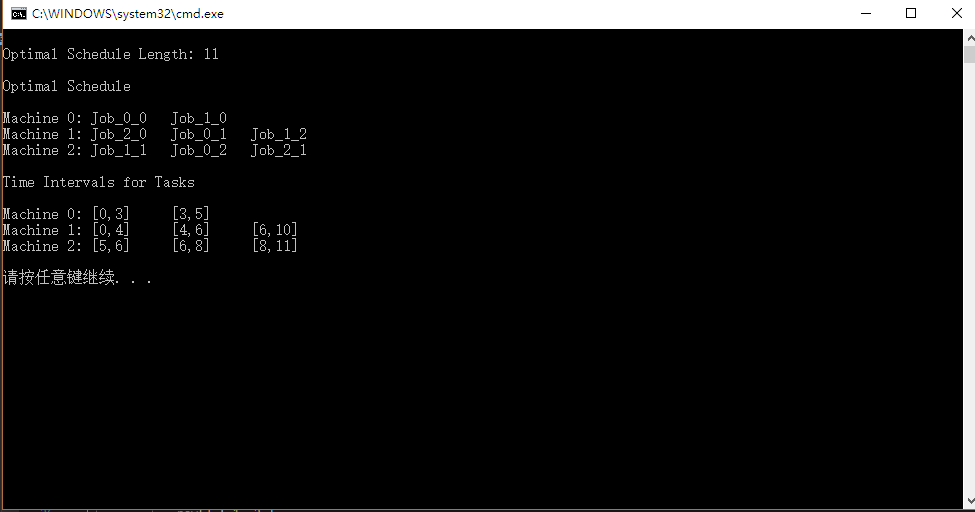
可以看到，这一次求得了最优解，与前面给的示范的结果不一样了，总时长上更少，是11而不是12了。对应的图解是这样：

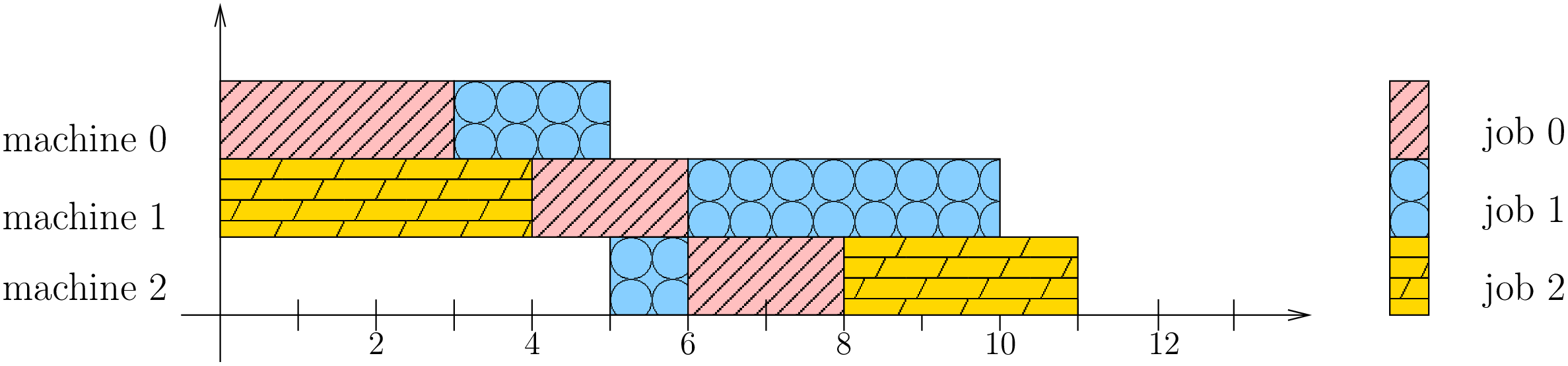
是不是觉得很有趣，跃跃欲试了！动手做就是最好的开始。

最后放出完整代码：

using Google.OrTools.ConstraintSolver;
using System;
using System.Collections.Generic;
using System.Linq;
 
public class ConsoleApp1
{
    static void Main()
    {
        // 创建约束求解器.
        var solver = new Solver("jobshop");
        var machines_count = ;
        var jobs_count = ;
        var all_machines = Enumerable.Range(, machines_count);
        var all_jobs = Enumerable.Range(, jobs_count);
 
        // 将任务拆分成对应的机器和用时的结构
        // job 0 = [(0, 3), (1, 2), (2, 2)]
        // job 1 = [(0, 2), (2, 1), (1, 4)]
        // job 2 = [(1, 4), (2, 3)]
        var machines = new int[][]
        {
            new[] { , ,  },
            new[] { , ,  },
            new[] { ,  }
        };
 
        var processing_times = new int[][]
        {
            new[] { , ,  },
            new[] {, ,  },
            new[] { ,  }
        };
 
        // 计算总用时
        var horizon = ;
        foreach (var i in all_jobs)
            horizon += processing_times[i].Sum();
 
        // 创建工序变量
        var all_tasks = new Dictionary<(int, int), IntervalVar>();
        foreach (var i in all_jobs)
        {
            foreach (var j in Enumerable.Range(, machines[i].Length))
            {
                all_tasks[(i, j)] = solver.MakeFixedDurationIntervalVar(,
                                                          horizon,
                                                          processing_times[i][j],
                                                          false,
                                                          $"Job_{i}_{j}");
            }
        }
 
        // 创建连接的顺序变量及连接关系
        var all_sequences = new SequenceVarVector();
        //var all_machines_jobs = new List<IntervalVar>();
        foreach (var i in all_machines)
        {
            var machines_jobs = new IntervalVarVector();
            foreach (var j in all_jobs)
            {
                foreach (var k in Enumerable.Range(, machines[j].Length))
                {
                    if (machines[j][k] == i)
                    {
                        machines_jobs.Add(all_tasks[(j, k)]);
                    }
                }
            }
            var disj = solver.MakeDisjunctiveConstraint(machines_jobs, $"machine {i}");
            all_sequences.Add(disj.SequenceVar());
            solver.Add(disj);
        }
 
        // 定义连接约束
        foreach (var i in all_jobs)
        {
            foreach (var j in Enumerable.Range(, machines[i].Length - ))
            {
                solver.Add(all_tasks[(i, j + )].StartsAfterEnd(all_tasks[(i, j)]));
            }
        }
 
        // 创建求解的极值目标
        var end_tasks = new IntVarVector();
        foreach (var i in all_jobs)
        {
            end_tasks.Add(all_tasks[(i, machines[i].Length - )].EndExpr().Var());
        }
        var obj_var = solver.MakeMax(end_tasks);
        var objective_monitor = solver.MakeMinimize(obj_var.Var(), );
 
        // 创建求解的对象
        var sequence_phase = solver.MakePhase(all_sequences.ToArray(), Solver.SEQUENCE_DEFAULT);
        var vars_phase = solver.MakePhase(new[] { obj_var.Var() }, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);
        var main_phase = solver.Compose(new[] { sequence_phase, vars_phase });
 
        // 创建最后一个解决方案
        var collector = solver.MakeLastSolutionCollector();
 
        // 添加需要关注的变量
        collector.Add(all_sequences.ToArray());
        collector.AddObjective(obj_var.Var());
 
        foreach (var i in all_machines)
        {
            var sequence = all_sequences[i];
            var sequence_count = sequence.Size();
            for (var j = ; j < sequence_count; j++)
            {
                var t = sequence.Interval(j);
                collector.Add(t.StartExpr().Var());
                collector.Add(t.EndExpr().Var());
            }
        }
 
        // 显示结果
        var disp_col_width = ;
        if (solver.Solve(main_phase, new SearchMonitor[] { objective_monitor, collector }))
        {
            Console.WriteLine("\nOptimal Schedule Length: {0}\n", collector.ObjectiveValue());
            var sol_line = "";
            var sol_line_tasks = "";
            Console.WriteLine("Optimal Schedule\n");
 
            foreach (var i in all_machines)
            {
                var seq = all_sequences[i];
                sol_line += $"Machine {i}: ";
                sol_line_tasks += $"Machine {i}: ";
                var sequence = collector.ForwardSequence(, seq);
                var seq_size = sequence.Count;
 
                foreach (var j in Enumerable.Range(, seq_size))
                {
                    var t = seq.Interval(sequence[j]);
                    sol_line_tasks += t.Name().PadRight(disp_col_width, ' ');
                }
 
                foreach (var j in Enumerable.Range(, seq_size))
                {
                    var t = seq.Interval(sequence[j]);
                    var sol_tmp = $"[{collector.Value(0, t.StartExpr().Var())},{collector.Value(0, t.EndExpr().Var())}]";
                    sol_line += sol_tmp.PadRight(disp_col_width, ' ');
                }
                sol_line += "\n";
                sol_line_tasks += "\n";
            }
            Console.WriteLine(sol_line_tasks);
            Console.WriteLine("Time Intervals for Tasks\n");
            Console.WriteLine(sol_line);
        }
    }
}