python 冒泡法 排序

冒泡排序

冒泡排序（Bubble Sort）：重复地遍历要排序的数列，依次比较两个元素，如果他们的顺序不符就把他们交换过来。就像气泡一样，需要排序的元素通过比较、交换位置，一点一点浮到对应的位置。

个人理解的原理：

　　1、比较相邻的元素。例：需要进行升序排列，如果：元素1 > 元素2   那么元素1和元素2就互换位置。（每次比较就像一个小步骤）

　　2、依次对每一对相邻元素比较，从第一对到最后一对。每次完成后就把最大的元素排到当次的最后了。（这样就完成了一个大步骤）

　　3、重复从头开始进行1、2的内容，但是因为前一次的比较后，都会有一个元素的位置确定，所以需要比较的元素会越来越少。

个人小节：

　　升序就每次循环把最大的排每次循环的后面

　　降序排列，就是每次循环把最小的排每次循环的最后面

list1 = [3, 5, 1, 2]  从左往右进行升序排列

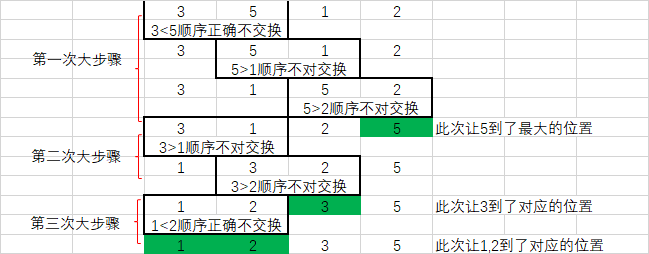
具体实现：

for i in range(len(list1)-1):    # 这个循环负责设置冒泡排序进行(大步骤)的次数
    for index in range(len(list1)-i-1):  # 负责每个小步骤的进行，并提供索引
        if list1[index] > list1[index+1]:
            list1[index], list1[index+1] = list1[index+1], list1[index]
    print(list1)