洛谷 P1436 棋盘分割 解题报告

P1436 棋盘分割

题目描述

将一个8*8的棋盘进行如下分割：将原棋盘割下一块矩形棋盘并使剩下部分也是矩形，再将剩下的两部分中的任意一块继续如此分割，这样割了(n-1)次后，连同最后剩下的矩形棋盘共有n块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行)

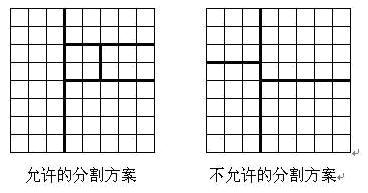
原棋盘上每一格有一个分值，一块矩形棋盘的总分为其所含各格分值之和。现在需要把棋盘按上述规则分割成n块矩形棋盘，并使各矩形棋盘总分的平方和最小。

请编程对给出的棋盘及n，求出平方和的最小值。

输入输出格式

输入格式：

第1行为一个整数n(1 < n < 15)。

第2行至第9行每行为8个小于100的非负整数，表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。

输出格式：

仅一个数，为平方和。

---

大力区间DP

\(dp[i][j][k][l][dep]\)表示左上角坐标为\((i,j)\),右下角为\((k,l)\)的矩形在处于第\(dep\)次切割时产生的答案

我打的是记忆化搜索

---

Code:

#include <cstdio>
#include <cstring>
const int inf=0x3f3f3f3f;
int min(int x,int y){return x<y?x:y;}
int n,score[9][9],f[9][9],dp[9][9][9][9][16];//左上角，右下角
int get(int i,int j,int k,int l)
{
    return f[k][l]-f[k][j-1]-f[i-1][l]+f[i-1][j-1];
}
int dfs(int x1,int y1,int x2,int y2,int dep)
{
    if(~dp[x1][y1][x2][y2][dep]) return dp[x1][y1][x2][y2][dep];
    dp[x1][y1][x2][y2][dep]=inf;
    for(int i=x1;i<x2;i++)
    {
        dp[x1][y1][x2][y2][dep]=min(dp[x1][y1][x2][y2][dep],dfs(x1,y1,i,y2,dep+1)+get(i+1,y1,x2,y2)*get(i+1,y1,x2,y2));
        dp[x1][y1][x2][y2][dep]=min(dp[x1][y1][x2][y2][dep],dfs(i+1,y1,x2,y2,dep+1)+get(x1,y1,i,y2)*get(x1,y1,i,y2));
    }
    for(int i=y1;i<y2;i++)
    {
        dp[x1][y1][x2][y2][dep]=min(dp[x1][y1][x2][y2][dep],dfs(x1,y1,x2,i,dep+1)+get(x1,i+1,x2,y2)*get(x1,i+1,x2,y2));
        dp[x1][y1][x2][y2][dep]=min(dp[x1][y1][x2][y2][dep],dfs(x1,i+1,x2,y2,dep+1)+get(x1,y1,x2,i)*get(x1,y1,x2,i));
    }
    return dp[x1][y1][x2][y2][dep];
}
int main()
{
    scanf("%d",&n);
    memset(dp,-1,sizeof(dp));
    for(int i=1;i<=8;i++)
        for(int j=1;j<=8;j++)
        {
            scanf("%d",&score[i][j]);
            f[i][j]=f[i-1][j]+f[i][j-1]-f[i-1][j-1]+score[i][j];
        }
    for(int i=1;i<=8;i++)
        for(int j=1;j<=8;j++)
            for(int k=1;k<=8;k++)
                for(int l=1;l<=8;l++)
                    dp[i][j][k][l][n]=get(i,j,k,l)*get(i,j,k,l);
    printf("%d\n",dfs(1,1,8,8,1));
    return 0;
}

---

2018.7.11