容斥原理&&莫比乌斯专题

A题：A - Eddy's爱好   HDU - 2204

具体思路：如果是求n中，为平方数的有多少个，那么答案肯定是sqrt（n）,同理，如果是三次根号的话，那么答案肯定是n的三分之一次方。然后继续按照这个思路来，对于1e18次方的数，最多就是2的64次方，也就是说我们最多枚举大小不超过63的素数就可以了，然后还需要考虑一种情况，比如说6的时候，被素数2算了一遍，然后又被素数3算了一遍，这个地方会有重复的计算，又因为2^(3*5*7)已经超过2的60次方了，所以我们只需要考虑三部分就可以了。

AC代码（1）：

 #include <iostream>
 #include <string>
 #include <deque>
 #include <stack>
 #include<cmath>
 #include <algorithm>
 #include<cstring>
 #include<stdio.h>
 #include<map>
 using namespace std;
 # define ll long long
 # define inf 0x3f3f3f3f
 # define ll_inf 1ll<<
 const int maxn = 1e6+;
 ll prim[]= {,,,,,,,,,,,,,,,,,};
 ll cal(ll t)
 {
     ll sum=;
     for(int i=;; i++)
     {
         ll tmp=pow(t,1.0/(prim[i]*1.0));
         if(tmp<)
             break;
         sum+=tmp-;
         for(int j=i+;; j++)
         {
             tmp=pow(t,1.0/(prim[i]*prim[j]*1.0));
             if(tmp<)
                 break;
             sum-=tmp-;
             for(int k=j+;; k++)
             {
                 tmp=pow(t,1.0/(prim[i]*prim[j]*prim[k]*1.0));
                 if(tmp<)
                     break;
                 sum+=tmp-;
             }
         }
     }
     return sum;
 }
     int main()
     {
         ll tmp;
         while(cin>>tmp)
         {
             cout<<cal(tmp)<<endl;
         }
         return ;
     }

AC代码（2）：

我们可以利用莫比乌斯系数进行简化计算，在上一个版本中，我们是按照奇加偶减的原则来进行的，同样这个计算的过程可以通过莫比乌斯中的mu函数来直接算出，每次相乘的系数是-mu[i]。

 #include <iostream>
 #include <string>
 #include <deque>
 #include <stack>
 #include<cmath>
 #include <algorithm>
 #include<cstring>
 #include<stdio.h>
 #include<map>
 using namespace std;
 # define ll long long
 # define inf 0x3f3f3f3f
 # define ll_inf 1ll<<
 const int maxn = +;
 ll mu[maxn*],prim[maxn*],check[maxn*];
 int tot=;
 void getmu()
 {
     mu[]=;
     for(int i=; i<maxn; i++)
     {
         // cout<<i<<endl;
         if(!check[i])
         {
             prim[tot++]=i;
             mu[i]=-;
         }
         for(int j=; j<tot; j++)
         {
             // cout<<i<<endl;
             if(prim[j]>maxn/i)
             {
                 break;
             }
             check[i*prim[j]]=;
             if(i%prim[j]==)
             {
                 mu[i*prim[j]]=;
                 break;
             }
             else
             {
                 mu[i*prim[j]]=-mu[i];
             }
         }
     }
     // cout<<1<<endl;
 }
 int main()
 {
     getmu();
     ll tmp;
     while(cin>>tmp)
     {
         ll sum=;
         for(ll  i=; i<=; i++)
         {
             sum-=mu[i]*(ll)(pow(tmp*1.0,1.0/i)-);
         }
         cout<<sum<<endl;
     }
     return ;
 }

B题：

题目链接：

B - How many integers can you find

HDU - 1796

题目大意：输入n，m.然后再输入m个数，问你1-(n-1)中，是这些数中任意个倍数的有多少？

具体思路：我们可以运用容斥的原理，最终答案等于sum=（能被一个数整除）-（能被两个数整除）+（能被三个数整除）-------.然后按照这个思路，我们运用二进制枚举直接暴力就可以了。 （int会爆掉）

AC代码：

 #include<iostream>
 #include<stack>
 #include<iomanip>
 #include<cstring>
 #include<string>
 #include<cmath>
 #include<algorithm>
 #include<stdio.h>
 using namespace std;
 # define int long long
 const int maxn = +;
 int a[maxn];
 int gcd(int a,int b){
 if(a<b)swap(a,b);
 return a%b==?b:gcd(b,a%b);
 }
 int lcm(int a,int b)
 {
     return a*b/gcd(a,b);
 }
 int cal(int n,int t)
 {
     int ans=;
     int maxstate=(<<t)-;
     for(int i=; i<=maxstate; i++)
     {
         int ind=;
         int tmp=;
         for(int j=; j<=t; j++)
         {
             if((<<j)&i)
             {
                 ind++;
                 tmp=lcm(tmp,a[j+]);
             }
         }
         ans-=mu[tmp]*(n/tmp);//其实这个地方也可以直接通过一个莫比乌斯中的mu函数求，但是这样的话mu函数就需要求的比较大，所以对于这个题还是建议下面这个方法，按照容斥原理。
         if(ind&)
         {
             ans+=n/tmp;
         }
         else
             ans-=n/tmp;
     }
     return ans;
 }
 signed main()
 {
     int n,m;
     while(cin>>n>>m)
     {
         int tot=;
         int tmp;
         n--;
         for(int i=; i<=m; i++)
         {
             cin>>tmp;
             if(!tmp)
                 continue;
             a[++tot]=tmp;
         }
         int ans=cal(n,tot);
         cout<<ans<<endl;
     }
  //   return 0;
 }
 //ll mu[maxn+100],prim[maxn+100],check[maxn+100];
 //void getmu()
 //{
 //    int tot=0;
 //    mu[1]=1;
 //    for(int i=2; i<maxn; i++)
 //    {
 //        if(!check[i])
 //        {
 //            prim[tot++]=i;
 //            mu[i]=-1;
 //        }
 //        for(int j=0; j<tot; j++)
 //        {
 //            if(prim[j]>maxn/i)
 //            {
 //                break;
 //            }
 //            check[i*prim[j]]=1;
 //            if(i%prim[j]==0)
 //            {
 //                mu[i*prim[j]]
 //                    =0;
 //                break;
 //            }
 //            else
 //            {
 //                mu[i*prim[j]]=-mu[i];
 //            }
 //        }
 //    }
 //}
 //int main()
 //{
 //    getmu();
 //    ll n,m;
 //    while(~scanf("%lld %lld",&n,&m))
 //    {
 //        ll minn=1ll<<60,maxx=0;
 //        ll tmp=0;
 //        n--;
 //        for(int i=1; i<=m; i++)
 //        {
 //            scanf("%lld",&tmp);
 //            maxx=max(maxx,tmp);
 //            minn=min(minn,tmp);
 //        }
 //        ll sum=1;
 //        for(int i=minn; i<=maxx; i++)
 //        {
 //            sum-=mu[i]*(n/i);
 //        }
 //        cout<<sum<<endl;
 //           printf("%lldn")
 //    }
 //}

C题：

C - Visible Trees

HDU - 2841

题目大意：给你一个n*m的图，你站在（0.0）这个点上，这个田地上从）（1,1）这个点开始有树，如果一个树和另外树在一条一个直线，这个时候后面那棵树就会看不到，然后问你这个人能看到多少树？

具体思路：首先来分析一波，如果一个树能被这个人看到，也就是说不会有别的树挡住当前这棵树，再分析到这棵树的坐标，也就说这个树的坐标不会被分解，也就说这个树的坐标x和y互素，分析到这里就可以了。我们只需要判断给定的（x，y）,(1,x)和（1，y）这段区间互素的数有多少就可以了。莫比乌斯反演、、

计算过程：

然后对于当前这个题,选择(1,b),(1,d) 中满足gcd(x,y)==1的对数,(1<=x<=b),(1<=y<=d) .

也就是说 gcd(x,y)==1满足的对数.

然后再开始分析一波:

我们令f(k)为满足(a,b),(c,d)中的gcd为1的对数.然后F(1)就是满足(a,b),(c,d)中的gcd为k的倍数的对数.

F(k)就等于(b/k)*(d/k).

f（1）= .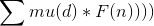

AC代码：

 #include<iostream>
 #include<stack>
 #include<iomanip>
 #include<cstring>
 #include<string>
 #include<cmath>
 #include<algorithm>
 #include<stdio.h>
 using namespace std;
 const int maxn = +;
 # define int long long
 int a[maxn];
 int mu[maxn+],prim[maxn+],check[maxn+];
 void getmu()
 {
     int tot=;
     mu[]=;
     for(int i=; i<maxn; i++)
     {
         if(!check[i])
         {
             prim[tot++]=i;
             mu[i]=-;
         }
         for(int j=; j<tot; j++)
         {
             if(prim[j]>maxn/i)
             {
                 break;
             }
             check[i*prim[j]]=;
             if(i%prim[j]==)
             {
                 mu[i*prim[j]]
                     =;
                 break;
             }
             else
             {
                 mu[i*prim[j]]=-mu[i];
             }
         }
     }
 }
 signed main()
 {
     getmu();
     int T;
     int n,m;
     cin>>T;
     while(T--)
     {
         cin>>n>>m;
         int sum=;
         int minn=min(n,m);
         for(int i=; i<=minn; i++)
         {
             sum+=mu[i]*(n/i)*(m/i);
         }
         cout<<sum<<endl;
     }
     return ;
 }
 D题：

 #include<iostream>
 #include<stack>
 #include<iomanip>
 #include<cstring>
 #include<string>
 #include<cmath>
 #include<algorithm>
 #include<stdio.h>
 using namespace std;
 const int maxn = 1e6+;
 # define ll long long
 ll a[maxn];
 ll mu[maxn+],prim[maxn+],check[maxn+];
 void getmu()
 {
     int tot=;
     mu[]=;
     for(int i=; i<maxn; i++)
     {
         if(!check[i])
         {
             prim[tot++]=i;
             mu[i]=-;
         }
         for(int j=; j<tot; j++)
         {
             if(prim[j]>maxn/i)
             {
                 break;
             }
             check[i*prim[j]]=;
             if(i%prim[j]==)
             {
                 mu[i*prim[j]]
                     =;
                 break;
             }
             else
             {
                 mu[i*prim[j]]=-mu[i];
             }
         }
     }
 }
 int main()
 {
     getmu();
     int T;
     cin>>T;
     int Case=;
     while(T--)
     {
         ll  x1,y1,x2,y2;
         cin>>x1>>y1>>x2>>y2;
         ll k;
         cin>>k;
         if(k==){
                         printf("Case %d: %lld\n",++Case,);
         }
         else {

         y1/=k;
         y2/=k;
         ll sum1=,sum2=;
         ll minn=min(y1,y2);
         for(int i=; i<=minn; i++)
         {
             sum1+=mu[i]*(y1/i)*(y2/i);
             sum2+=mu[i]*(minn/i)*(minn/i);
         }
         printf("Case %d: %lld\n",++Case,sum1-sum2/);
         }
     }
     return ;
 }