【IUML】支持向量机SVM[续]
支持向量机基本上是最好的有监督学习算法了。看很多正统的讲法都是从VC 维理论和结构风险最小原理出发,然后引出SVM什么的,还有些资料上来就讲分类超平面什么的。我们logistic回归出发,引出了SVM,既揭示了模型间的联系,也让人觉得过渡更自然。
logistic回归
Logistic回归目的是从特征学习出一个0/1分类模型,而这个模型是将特性的线性组合作为自变量,由于自变量的取值范围是负无穷到正无穷。因此,使用logistic函数(或称作sigmoid函数)将自变量映射到(0,1)上,映射后的值被认为是属于y=1的概率。形式化表示就是假设函数
其中x是n维特征向量,函数g就是logistic函数。
图像如下所示:
可以看到,将无穷映射到了(0,1)。而假设函数就是特征属于y=1的概率。
当我们要判别一个新来的特征属于哪个类时,只需求
再审视一下






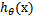 =1,反之
=1,反之




图形化表示如下:

中间那条线是
形式化表示
我们这次使用的结果标签是y=-1,y=1,替换在logistic回归中使用的y=0和y=1。同时将





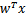 )。这样,我们让
)。这样,我们让

上一节提到过我们只需考虑
函数间隔(functional margin)和几何间隔(geometric margin)
给定一个训练样本
可想而知,当







刚刚我们定义的函数间隔是针对某一个样本的,现在我们定义全局样本上的函数间隔
说白了就是在训练样本上分类正例和负例确信度最小那个函数间隔。接下来定义几何间隔,先看图
假设我们有了B点所在的





进一步得到
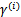 实际上就是点到平面距离。
实际上就是点到平面距离。
再换种更加优雅的写法:
当


最优间隔分类器(optimal margin classifier)
回想前面我们提到我们的目标是寻找一个超平面,使得离超平面比较近的点能有更大的间距。也就是我们不考虑所有的点都必须远离超平面,我们关心求得的超平面能够让所有点中离它最近的点具有最大间距。形象的说,我们将上面的图看作是一张纸,我们要找一条折线,按照这条折线折叠后,离折线最近的点的间距比其他折线都要大。形式化表示为:
这里用

到此,我们已经将模型定义出来了。如果求得了w和b,那么来一个特征x,我们就能够分类了,称为最优间隔分类器。接下的问题就是如何求解w和b的问题了。
由于

这时候其实我们求的最大值仍然是几何间隔,只不过此时的w不受
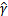 做一些限制,以保证我们解是唯一的。这里为了简便我们取
做一些限制,以保证我们解是唯一的。这里为了简便我们取



只有线性约束了,而且是个典型的二次规划问题(目标函数是自变量的二次函数)。代入优化软件可解。到这里发现,画好分类超平面,在图上标示出间隔那么直观,但每一步推导有理有据,依靠思路的流畅性来推导出目标函数和约束。
======================================================== 转载请注明出处:http://blog.csdn.net/utimes/article/details/9259301 ========================================================【IUML】支持向量机SVM[续]的更多相关文章
- 【IUML】支持向量机SVM
从1995年Vapnik等人提出一种机器学习的新方法支持向量机(SVM)之后,支持向量机成为继人工神经网络之后又一研究热点,国内外研究都很多.支持向量机方法是建立在统计学习理论的VC维理论和结构风险最 ...
- 机器学习——支持向量机SVM
前言 学习本章节前需要先学习: <机器学习--最优化问题:拉格朗日乘子法.KKT条件以及对偶问题> <机器学习--感知机> 1 摘要: 支持向量机(SVM)是一种二类分类模型, ...
- 机器学习:Python中如何使用支持向量机(SVM)算法
(简单介绍一下支持向量机,详细介绍尤其是算法过程可以查阅其他资) 在机器学习领域,支持向量机SVM(Support Vector Machine)是一个有监督的学习模型,通常用来进行模式识别.分类(异 ...
- 以图像分割为例浅谈支持向量机(SVM)
1. 什么是支持向量机? 在机器学习中,分类问题是一种非常常见也非常重要的问题.常见的分类方法有决策树.聚类方法.贝叶斯分类等等.举一个常见的分类的例子.如下图1所示,在平面直角坐标系中,有一些点 ...
- 机器学习算法 - 支持向量机SVM
在上两节中,我们讲解了机器学习的决策树和k-近邻算法,本节我们讲解另外一种分类算法:支持向量机SVM. SVM是迄今为止最好使用的分类器之一,它可以不加修改即可直接使用,从而得到低错误率的结果. [案 ...
- 机器学习之支持向量机—SVM原理代码实现
支持向量机—SVM原理代码实现 本文系作者原创,转载请注明出处:https://www.cnblogs.com/further-further-further/p/9596898.html 1. 解决 ...
- 支持向量机SVM——专治线性不可分
SVM原理 线性可分与线性不可分 线性可分 线性不可分-------[无论用哪条直线都无法将女生情绪正确分类] SVM的核函数可以帮助我们: 假设‘开心’是轻飘飘的,“不开心”是沉重的 将三维视图还原 ...
- 一步步教你轻松学支持向量机SVM算法之案例篇2
一步步教你轻松学支持向量机SVM算法之案例篇2 (白宁超 2018年10月22日10:09:07) 摘要:支持向量机即SVM(Support Vector Machine) ,是一种监督学习算法,属于 ...
- 一步步教你轻松学支持向量机SVM算法之理论篇1
一步步教你轻松学支持向量机SVM算法之理论篇1 (白宁超 2018年10月22日10:03:35) 摘要:支持向量机即SVM(Support Vector Machine) ,是一种监督学习算法,属于 ...
随机推荐
- Ionic Tabs
Ionic 默认的 Tabs 模板 ,Android的在上方,IOS的在下方.在www/js/app.js修改配置,添加一个变量,再修改相应属性: .config(function($statePro ...
- iuap
2017.12 用友今年着力点往云平台发展,是时候整理一下思路 第一:iuap 第二:Linux 第三:财务会计业务入门 第四:NC节点视频教程--财务模块 2019年3月4日 all in iuap ...
- matplotlib 中文显示 的问题
第一种方法 from pylab import mpl import numpy as np mpl.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体 ...
- scrapy爬虫,爬取图片
一.scrapy的安装: 本文基于Anacoda3, Anacoda2和3如何同时安装? 将Anacoda3安装在C:\ProgramData\Anaconda2\envs文件夹中即可. 如何用con ...
- Django-高级特性
分页 1.固定显示分页数目 2.点击相应分页取出对应数据 具体实现: from django.utils.safestring import mark_safe class Pagination(ob ...
- android studio 汉化包 美化包
韩梦飞沙 韩亚飞 313134555@qq.com yue31313 han_meng_fei_sha 汉化包 百度云盘 下载地址:https://pan.baidu.com/s/1pLjwy ...
- android 打开 res raw目录 中 数据库文件
韩梦飞沙 韩亚飞 313134555@qq.com yue31313 han_meng_fei_sha 安卓不能直接打开 res raw 中的 数据库 文件. 通过 资源 获取资源 方法 , ...
- loj#2718. 「NOI2018」归程
题目链接 loj#2718. 「NOI2018」归程 题解 按照高度做克鲁斯卡尔重构树 那么对于询问倍增找到当前点能到达的高度最小可行点,该点的子树就是能到达的联通快,维护子树中到1节点的最短距离 s ...
- BZOJ.4552.[HEOI2016/TJOI2016]排序(线段树合并/二分 线段树)
题目链接 对于序列上每一段连续区间的数我们都可以动态开点建一棵值域线段树.初始时就是\(n\)棵. 对于每次操作,我们可以将\([l,r]\)的数分别从之前它所属的若干段区间中分离出来,合并. 对于升 ...
- SPOJ GSS
GSS1 题目大意:给出一个数列,多次询问区间最长连续子段和 题解:线段树维护区间最长连续子段和gss,区间从最左元素开始的最长连续子段和lgss 区间以最右元素为结尾的最长连续子段和rgss以及区间 ...















