Table.Group分组…Group（Power Query 之 M 语言）

数据源：

　　10列55行数据，其中包括含有重复项的“部门”列和可求和的“金额”列。

目标：

　　按“部门”列进行分组，显示各部门金额小计。

操作过程：

　　【主页】》【分组依据】》“部门”》新列名“金额小计”》操作【求和】》柱“金额”

　　【转换】》【分组依据】》“部门”》新列名“金额小计”》操作【求和】》柱“金额”

M公式：

　　= Table.Group( 表, { "分级列1",…, "分级列n"},{{ "新列名1", 函数1, 数据类型1},…,{ "新列名n",  函数n, 数据类型n}}, 分组模式, 自定义分组条件)

　　　　为“分列级”去除重复项：= Table.Group( 表, "分列级", {})

　　　　将表转换成一个组：= Table.Group( 表, {},{ "新列名", each _})

说明：

　　分组模式

　　　　0：局部模式，按分级列进行分类汇总

　　　　1/缺省：全局模式，将分级列排序后再进行分类汇总

最终效果：

 

扩展：

　　= Table.FuzzyGroup( 表, { "分级列1",…, "分级列n"},{{ "新列名1", 函数1, 数据类型1},…,{ "新列名n",  函数n, 数据类型n}}, 设定条件)

　　　　示例，如图中所示进行分组，结果不理想：

　　　　　　换成Fuzzy会有意想不到的收获：

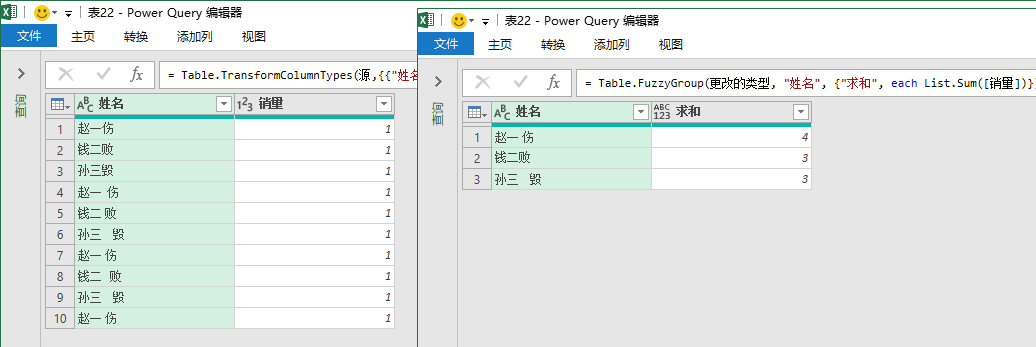
　　　　　　（当然，完全指望电脑来判断也是不太现实的……）

　　　　设定条件：

　　　　　　[IgnoreCase = true / false]：true或缺省时区分大小写

　　　　　　[IgnoreSpace = true / false]：true或缺省时忽略空格（其实只是针对蚯蚓文）

　　　　　　还有几个，好像用处不大，话说上面两个貌似用处也……咳咳……不大……