Missing Data in Kernel PCA

引
主要内容
- 关于缺失数据的导数
附录
- 极大似然估计
代码

Sanguinetti G, Lawrence N D. Missing data in kernel PCA[J]. european conference on machine learning, 2006: 751-758.

引

普通的kernel PCA是通过$K$，其中$K_{ij} = \Phi^T(y_i) \Phi(y_j)$来获得，很显然，如果数据有缺失，就不能直接进行kernel PCA了，这篇文章所研究的问题就是，在数据有缺失的情况下，该怎么进行kernel PCA。

这篇文章的亮点，在我看来，是将kernel PCA和数据缺失结合起来。把kernel 去掉，已经有现存的文章了，至少那篇PPCA就是一个例子吧。kernel的作用就是，非显示地将样本映射到高维空间，所以，就得想办法把这玩意儿给造出来。

假设样本已经中心化。

主要内容

在PPCA中，每个样本服从：

\[y_i = W x_i + \epsilon
\]

其中$y_i \in \mathbb{R}^d$为样本，$x_i \in \mathbb{R}^q$为隐变量，$W \in \mathbb{R}^{d \times q}， d > q$，$\epsilon \sim N(0, \sigma^2 I)$。

PPCA中，假设$x_i$服从一个正态分布，而作者是通过一个对偶，将$W$设置为随机向量，每个$w_{ij} \sim N(0,1)$（说实话，我对啥是对偶越来越晕了），通过将$W$积分掉，可得：

\[y^{(j)} \sim N(0, XX^T + \sigma^2I)
\]

其中，$y^{(j)}$是$Y$的第j列，$Y$的第i行是$y_i$，$X$的第i行是$x_i$。这个的证明和在贝叶斯优化中推导的证明是类似的，这里就不多赘述了。

其似然函数关于$X$求极大可以得到：

\[X = U \Lambda R
\]

其中$U$是$K=\frac{1}{d}YY^T$的特征向量，而

\[\Lambda = (V - \sigma^2 I)^{\frac{1}{2}}
\]

其中$V$是$U$所对应的特征值，而$R$是任意的正交矩阵。

虽然论文里没讲，但是$\sigma^2$d的估计应该是下面的这个吧：

\[\sigma^2 = \frac{1}{N-q}\sum_{i=q+1}^N \lambda_i
\]

这部分的推导见附录。

上面的过程可以这么理解，我们用$XX^T + \sigma^2 I$来近似$K$，因为实际上，似然函数有下面的形态（舍掉了一些常数）：

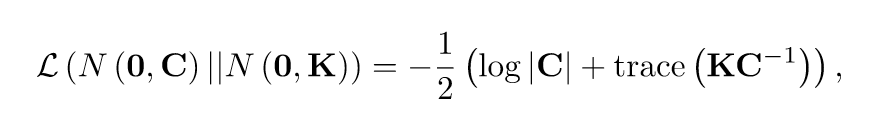
上面这个式子不仅是对数似然函数，也是交叉熵，交叉熵又和K-L散度(描述俩个分布之间距离的)有关，所以我们极大化似然函数的过程，实际上就是在找一个$K$的近似$C$。

直到现在，我们依然没有将kernel结合进去，注意到：

\[K = \frac{1}{d}YY^T
\]

$K_{ij} = \frac{1}{d}y_i^T y_j$，所以，对于任意的$\Phi(\cdot)$作用于$y_i$，

\[K_{ij} = \frac{1}{d}\Phi^T(y_i)\Phi(y_j)
\]

kernel PCA呼之预出，我们逼近$K$实际上就是去近似kernel PCA。

这里有一个假设，就是$y_i$是已知的，如果$y_i$是缺失的，那么我们没有办法找到$C$，现在的问题也就是有缺失数据的时候，如何进行kernel PCA。

根据上面的分析，很自然的一个想法就是，先通过插补补全数据，计算$K$，然后再计算$C$，这个时候，似然函数里面，将缺失数据视作变量，再关于其最小化交叉熵，反复迭代，直至收敛，便完成了缺失数据下的kernel PCA。我有点搞不懂为什么是最小化交叉熵了，如果我没理解错，这里的交叉熵是指-L吧。俩个分布的交叉熵如下：

\[-\int p(x) \ln q(x) \mathrm{d}x
\]

所以$N(0,K),N(0,C)$的交叉熵应该是-L。而且，我做了实验，至少只有极大化似然函数，结果才算让人满意。所以文章中的交叉熵应该是-L，所以我们要做的就是最小化交叉熵，最大化似然函数。

关于缺失数据的导数

假设$C$是已知的，$Y_{ij}$是缺失的，那么我们希望关于$Y_{ij}$最大化下式（擅作主张了）：

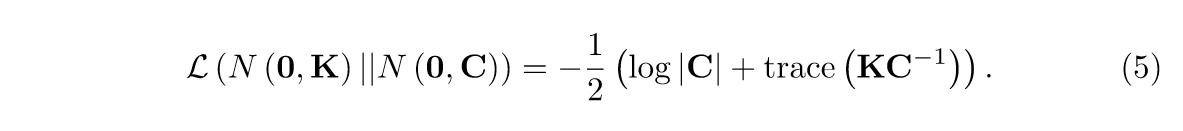
记$C^{-1}$的第$i$列(行)为$c$(因为是对称的)，假设kernel选择的是$k(x,y)=\exp \{-\frac{\gamma}{2}(||x-y||_2^2)\}$

\[\mathrm{d}K_{ik} = -\frac{\gamma}{d} \exp \{-\frac{\gamma}{2}\|Y_i-Y_k\|^2\}(Y_{ij}-Y_{kj}), \quad k \ne i
\]

\[\begin{array}{ll}
\mathrm{d}L &= -\frac{1}{2}\mathrm{Tr}(\mathrm{d}KC^{-1})\\
&= [\gamma \sum \limits_{k=1}^N K_{ik} (Y_{ij}-Y_{kj})c_k] \mathrm{d}Y_{ij} \\
&= [\gamma Y_{ij} K_i^T c - \gamma K_i^T diag(c)Y^{(j)}] \mathrm{d}Y_{ij}
\end{array}
\]

令其为0，可得：

\[K_i^TcY_{ij} = K_i^T diag(c)Y^{(j)}
\]

这个方程咋子解咯，而且是如果有不止一个缺失值不就凉凉了。

文章说用共轭梯度法，所以说没显示解？

附录

极大似然估计

容易知道，其对数似然函数为：

\[L = -\frac{Nd}{2} \ln 2\pi - \frac{d}{2} \ln |C| - \frac{d\mathrm{Tr}(C^{-1}K)}{2}
\]

其中$C = XX^T+\sigma^2 I$，容易获得：

\[\mathrm{d}L = -d\mathrm{Tr}(C^{-1}X \mathrm{d}X^T) + d \mathrm{Tr}(C^{-1}KC^{-1}XdX^T)
\]

所以，在满足下式的点中取得极值：

\[C^{-1}X = C^{-1}KC^{-1}X \\
\Rightarrow \quad KC^{-1}X = X
\]

$X = 0$，没有什么意义；

\[X = U\Lambda R
\]

此时$KC^{-1}X=X$,注意当$K$可逆的时候，此时$KC^{-1}=I$，但是当$K$不可逆的时候，需要用$K = \sum_{i=1}^l \lambda_i(K)u_i(K)u_i^T(K)$来考虑(不过凉凉的是，$\lambda_i \ge \sigma^2$好像就可能失效了)。

就是PPCA里面讲过的,令$X=U'L'V'^T$

\[KU'=U'(\sigma^2 L+L^2)
\]

即$U'$为$K$的特征向量，结果是类似的。

到这里，我们也只讲了什么点是能取得极值的候选点，为什么取得极值，还是没弄懂。

代码

在做实验的时候，对初始点，也就是缺失值的补全要求还是蛮高的，差20%就GG了，而且开始几步收敛很快，后面收敛超级慢，所以我不知道怎么设置收敛条件了。

import numpy as np

class MissingData:

    def __init__(self, data, index, q):

        """

        :param data:缺失数据集，缺失部分通过平均值补全

        :param index: ij==1表示缺失

        :param q: 隐变量的维度

        """

        self.__data = np.array(data, dtype=float)

        self.__index = index

        self.__n, self.__d = data.shape

        self.gamma = 1 #kernel的参数

        assert self.__d > q, "Invalid q"

        self.q = q

    @property

    def data(self):

        return self.__data

    @property

    def index(self):

        return self.__index

    @property

    def n(self):

        return self.__n

    @property

    def d(self):

        return self.__d

    def kernel(self, x, y, gamma):

        """kernel exp"""

        return np.exp(-gamma / 2 *

                      (x-y) @ (x-y))

    def compute_K(self):

        K = np.zeros((self.n, self.n))

        for i in range(self.n):

            x = self.data[i]

            for j in range(i, self.n):

                y = self.data[j]

                K[i, j] = K[j, i] = self.kernel(x, y, self.gamma)

        self.K = K / self.d

    def ordereig(self, A):

        """晕了，没想到linalg.eig出来的特征值不一定是按序的"""

        value, vector = np.linalg.eig(A)

        order = np.argsort(value)[::-1]

        value = value[order]

        vector = vector.T[order].T

        return value, vector

    def compute_C(self):

        value, vector = self.ordereig(self.K)

        value1 = value[:self.q]

        value1 = value1[value1 > 0]

        value2 = value[self.q:]

        U = vector[:, :len(value1)]

        sigma2 = np.mean(value2)

        self.X = U * np.sqrt(value1 - sigma2)

        self.C = self.X @ self.X.T + sigma2 * np.identity(self.n)

        self.invC = np.linalg.inv(self.C)

    def compute_unit(self, i, j):

        c = self.invC[i]

        return -self.gamma * (

            self.data[i, j] * self.K[i] @ c -

            (self.K[i] * c) @ self.data[:, j]

        )

    def compute_grad(self):

        """计算导数，但愿我的公式没推错"""

        delta = np.zeros((self.n, self.d), dtype=float)

        for i in range(self.n):

            for j in range(self.d):

                if self.index[i, j] == 1:

                    delta[i, j] = self.compute_unit(i, j)

        self.delta = delta

    def likehood(self, K):

        return 1 / 2 * np.trace(K @ self.invC)

    def temp_K(self, data):

        K = np.zeros((self.n, self.n), dtype=float)

        for i in range(self.n):

            x = data[i]

            for j in range(i, self.n):

                y = data[j]

                K[i, j] = K[j, i] = self.kernel(x, y, self.gamma)

        return K / self.d

    def backtrack(self, alpha=0.4, beta=0.7):

        """

        采用回溯梯度下降

        :param alpha:

        :param beta:

        :return:

        """

        count = 0

        time = 0

        self.compute_K()

        self.compute_C()

        self.compute_grad()

        norm = -np.sum(self.delta ** 2)

        t = 1

        L1 = self.likehood(self.K)

        while True:

            time += 1

            while True:

                count += 1

                data = self.data - self.delta * t

                tempK = self.temp_K(data)

                L2 = self.likehood(tempK)

                if L2 > L1 + alpha * t * norm:

                    t = beta * t

                else:

                    self.__data = np.array(data, dtype=float)

                    break

            delta = np.array(self.delta)

            self.compute_K()

            self.compute_grad()

            print(time, count, L1, L2)

            if np.sum((delta - self.delta) ** 2) < 1e-6:

                break

            norm = -np.sum(self.delta ** 2)

            t = 1

            L1 = self.likehood(self.K)

            count = 0

    def processing(self, alpha=0.4, beta=0.7):

        count = 0

        while count < 7: #我不知道怎么判断收敛就这么玩一玩吧

            count += 1

            print("**********{0}**********".format(count))

            self.backtrack(alpha, beta)