位运算符在JS中的妙用

正文

位运算

JavaScript 中最臭名昭著的 Bug 就是 0.1 + 0.2 !== 0.3，因为精度的问题，导致所有的浮点运算都是不安全的，具体原因可详见《0.1 + 0.2不等于0.3？为什么JavaScript有这种“骚”操作？》。

因此，之前有大牛提出，不要在 JS 中使用位运算：

Javascript 完全套用了 Java 的位运算符，包括按位与&、按位或|、按位异或^、按位非~、左移<<、带符号的右移>>和用0补足的右移>>>。 这套运算符针对的是整数，所以对 JavaScript 完全无用，因为 JavaScript 内部，所有数字都保存为双精度浮点数。如果使用它们的话，JavaScript 不得不将运算数先转为整数，然后再进行运算，这样就降低了速度。而且"按位与运算符"&同"逻辑与运算符"&&，很容易混淆。

但是在我看来，如果对 JS 的运用达到炉火纯青的地步，能避开各种“Feature”的话，偶尔用一下位运算符也无所谓，还能提升运算性能，毕竟直接操作的是计算机最熟悉的二进制。

位运算的原理可以参考这篇文章 《位运算符在JS中的妙用》

1. 使用左移运算符 << 迅速得出2的次方

1 << 2  // 4, 即 2的2次方
1 << 10 // 1024, 即 2的10次方

// 但是要注意使用场景
a = 2e9;   // 2000000000
a << 1;    // -294967296

2. 使用 ^ 切换变量 0 或 1

// --- before ---
// if 判断
if (toggle) {
    toggle = 0;
} else {
    toggle = 1;
}
// 三目运算符
togle = toggle ? 0 : 1;

// --- after ---
toggle ^= 1;

3. 使用 & 判断奇偶性

偶数 & 1 = 0

奇数 & 1 = 1

console.log(7 & 1);    // 1
console.log(8 & 1) ;   // 0

4. 使用 !! 将数字转为布尔值

所有非0的值都是true，包括负数、浮点数：

console.log(!!7);       // true
console.log(!!0);       // false
console.log(!!-1);      // true
console.log(!!0.71);    // true

5. 使用~、>>、<<、>>>、|来取整

相当于使用了 Math.floor()

console.log(~~11.71)     // 11
console.log(11.71 >> 0)  // 11
console.log(11.71 << 0)  // 11
console.log(11.71 | 0)   // 11
console.log(11.71 >>> 0) // 11

注意 >>> 不可对负数取整

6. 使用^来完成值交换

这个符号的用法前面提到过，下面介绍一些高级的用法，在 ES6 的解构赋值出来之前，用这种方式会更快(但必须是整数)：

// --- before ---
let temp = a; a = b; b = temp; // 传统，但需要借助临时变量
b = [a, a = b][0] // 借助数组

// --- after ---
let a = 7
let b = 1
a ^= b
b ^= a
a ^= b
console.log(a)   // 1
console.log(b)   // 7

[a, b] = [b, a]; // ES6，解构赋值

7. 使用^判断符号是否相同

(a ^ b) >= 0; //  true 相同; false 不相同

8. 使用^来检查数字是否不相等

// --- before ---
if (a !== 1171) {...};

// --- after ---
if (a ^ 1171) {...};

9. n & (n - 1)，如果为 0，说明 n 是 2 的整数幂

10. 使用 A + 0.5 | 0 来替代 Math.round()

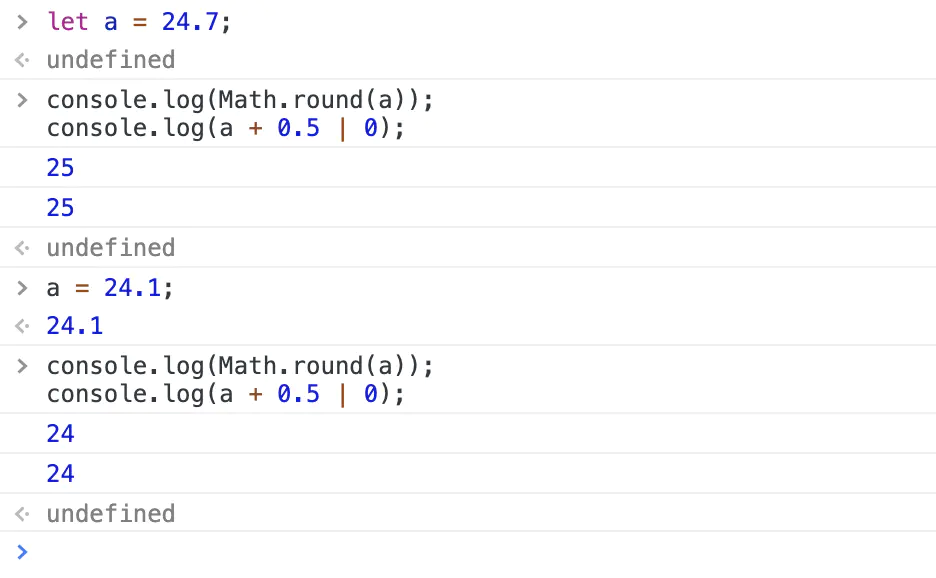
如果是负数，只需要-0.5

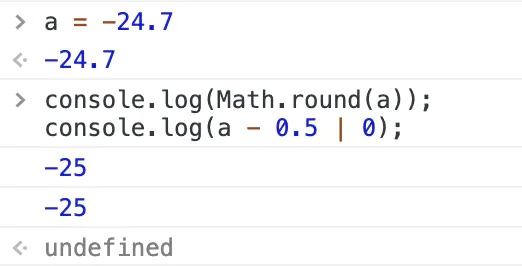
String

1. 使用toString(16)取随机字符串

Math.random().toString(16).substring(2, 15);

.substring() 的第二个参数控制取多少位 (最多可取13位)

2. 使用 split(0)

使用数字来做为 split 的分隔条件可以节省2字节

// --- before ---
"alpha,bravo,charlie".split(",");

// --- after ---
"alpha0bravo0charlie".split(0);

3. 使用.link() 创建链接

一个鲜为人知的方法，可以快速创建 a 标签

// --- before ---
let b = `<a herf="www.google.com">google</a>`;

// --- after ---
let b = 'google'.link('www.google.com');

3. 使用 Array 来重复字符

// --- before ---
for (let a = "", i = 7; i--;) a+= 0;

// --- after ---
let b = Array(7).join(0); // "000000"
let c = Array(7).join('La') // "LaLaLaLaLaLa"

// ES6
let d = "0".repeat(7); // "0000000"

其他一些花里胡哨的操作

1. 使用当前时间创建一个随机数

// --- before ---
let b = 0 | Math.random() * 100

// --- after ---
let a;
a = new Date % 100; // 两位随机数
a = new Date % 1000; // 三位随机数
a = new Date % 10000; // 四位随机数...依次类推
// 不要在快速循环中使用，因为毫秒可能没有变化；

2. 一些可以替代 undefined 的操作

1. ""._, 1.._ 和 0[0]

1. void 0 会比写 undefined 要快一些

let d = void 0;
console.log(d); // undefined

3. 使用 1/0 来替代 Infinity

// --- before ---
[Infinity, -Infinity]

// --- after ---
[1/0, -1/0]

4. 使用 Array.length = 0 来清空数组

5. 使用 Array.slice(0) 实现数组浅拷贝

6. 使用 !+"\v1" 快速判断 IE8 以下的浏览器

谷歌浏览器：

IE 9（10，11）：

IE 8（7，6，5）：

7. for 循环条件的简写

// --- before ---
for(let i = 0; i < arr.length; i++) {...}

// --- after ---
for(let i = arr.length; i--;) {...} // 注意 i-- 后面的分号别漏了

原文链接：https://juejin.im/post/5e044eb5f265da33b50748c8