noip模拟5[string·matrix·big·所驼门王的宝藏]

怎么说呢这一场考得还算可以呢

拿了120pts，主要是最后一个题灵光开窍，想起来是tarjan，然后勉勉强强拿了40pts，本来是可以拿满分的，害

没事考完了就要反思

这场考试我心态超好，从第一个题开始打暴力，一直打到第三题，嘿嘿自我感觉良好

不过我这个dfs的能力还是差了一点，得在磨练磨练！！！

要保持这种状态先打暴力，再想正解！！！加油！！！

那就是正解环节了。。。。

T1  string

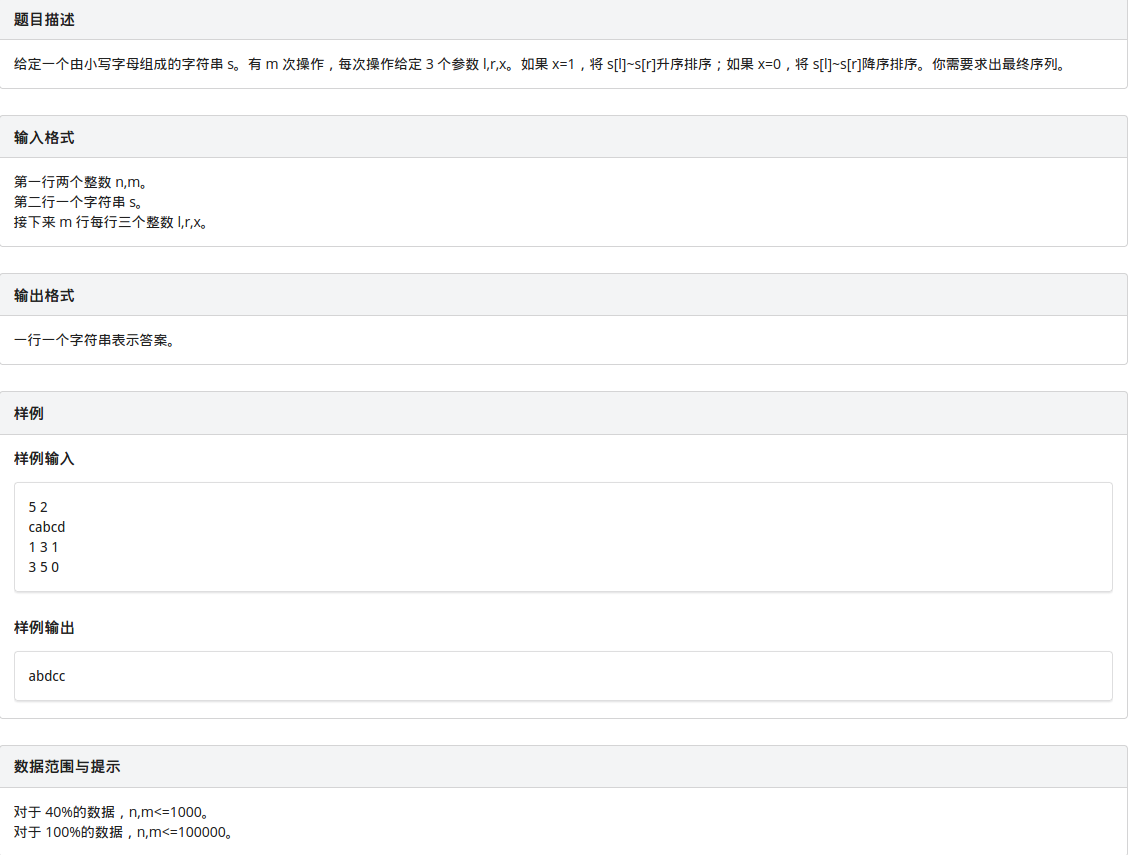
第一眼看到这个题，我说：：：暴力有分了，看我10min把它A了，来来来。。。

我就上了

#include<bits/stdc++.h>
using namespace std;
#define re register int
const int N=100005;
int n,m;
char ch[N];
signed main(){
    scanf("%d%d",&n,&m);
    scanf("%s",ch+1);
    for(re i=1;i<=m;i++){
        int l,r,x;
        scanf("%d%d%d",&l,&r,&x);
        if(x==1)sort(ch+l,ch+r+1);
        else sort(ch+l,ch+r+1,greater<char>());
    }
    for(re i=1;i<=n;i++)printf("%c",ch[i]);
}

sort大法好，直接拿到四十分，

于是就这样我们成功的打完了第一题，用时：7min

不扯了，上正解

我们发现，上面的代码复杂度是m*n*logn的

所以我们尽量省去一个n，m是肯定在这里的，搞不掉

大佬们说过一句话：

遇到线性问题时，我们要用线段树;　　

遇到树上的问题时，我们要用dfs序+线段树;

那这个题我们就尝试用线段树来解决问题;

一开始是这么想的，每个点就存这个点的字符就好了，后来发现我连线段树是啥都不知道了，竟然只维护点。。。

在每个点上加一个桶（这名词高大上吧！！就是开个数组，统计每个字符出现的次数）

然后就可以开开心心的用了

每一次排序，先把这个区间内的所有权值都提取出来，再一部分一部分的插入回去

一开始我觉得这样会T的吧，但是好像没有比这个更快的办法了

#include<bits/stdc++.h>
using namespace std;
#define re register int
#define mem(a) memset(a,0,sizeof(a))
const int N=100005;
int n,m;
char ch[N];
int num[N];
int now[27];
struct node{
    #define ls x<<1
    #define rs x<<1|1
    int val[N*4][27];
    int laz[N*4];
    inline void pushup(int x){
        for(re i=1;i<=26;i++)
            val[x][i]=val[ls][i]+val[rs][i];
    }
    inline void pushdown(int x,int l,int r){
        if(laz[x]){
            int mid=l+r>>1;
            laz[ls]=laz[x];
            laz[rs]=laz[x];
            mem(val[ls]);
            mem(val[rs]);
            val[ls][laz[x]]=mid-l+1;
            val[rs][laz[x]]=r-mid;
            laz[x]=0;
        }
    }
    inline void build(int x,int l,int r){
        if(l==r){
            val[x][num[l]]=1;
            //cout<<(char)(num[l]+'a'-1)<<" ";
            return ;
        }
        int mid=l+r>>1;
        build(ls,l,mid);
        build(rs,mid+1,r);
        pushup(x);
    }
    inline void ins(int x,int l,int r,int ql,int qr,int c){
        //if(ql>qr)return ;
        if(ql<=l&&r<=qr){
            laz[x]=c;
            mem(val[x]);
            val[x][c]=r-l+1;
            return ;
        }
        pushdown(x,l,r);
        int mid=l+r>>1;
        if(ql<=mid)ins(ls,l,mid,ql,qr,c);
        if(qr>mid)ins(rs,mid+1,r,ql,qr,c);
        pushup(x);
    }
    inline void query(int x,int l,int r,int ql,int qr){
        if(ql<=l&&r<=qr){
            for(re i=1;i<=26;i++)now[i]+=val[x][i];
            return ;
        }
        pushdown(x,l,r);
        int mid=l+r>>1;
        if(ql<=mid)query(ls,l,mid,ql,qr);
        if(qr>mid)query(rs,mid+1,r,ql,qr);
    }
    inline void dfs(int x,int l,int r){
        if(l==r){
            for(re i=1;i<=26;i++)
                if(val[x][i]){
                    printf("%c",i+'a'-1);
                    break;
                }
            return ;
        }
        pushdown(x,l,r);
        int mid=l+r>>1;
        dfs(ls,l,mid);
        dfs(rs,mid+1,r);
    }
    #undef ls
    #undef rs
}xds;
signed main(){
    scanf("%d%d",&n,&m);
    scanf("%s",ch+1);
    for(re i=1;i<=n;i++)num[i]=ch[i]-'a'+1;
    xds.build(1,1,n);
    for(re i=1;i<=m;i++){
        int l,r,x;
        scanf("%d%d%d",&l,&r,&x);
        mem(now);
        xds.query(1,1,n,l,r);
        if(x==1){
            for(re i=1;i<=26;i++){
                if(!now[i])continue;
                xds.ins(1,1,n,l,l+now[i]-1,i);
                l+=now[i];
            }
        }
        else{
            for(re i=26;i>=1;i--){
                if(!now[i])continue;
                xds.ins(1,1,n,l,l+now[i]-1,i);
                l+=now[i];
            }
        }
    }
    xds.dfs(1,1,n);
}

T1

过了这个题我觉得我又行了哈哈哈

T2   matrix

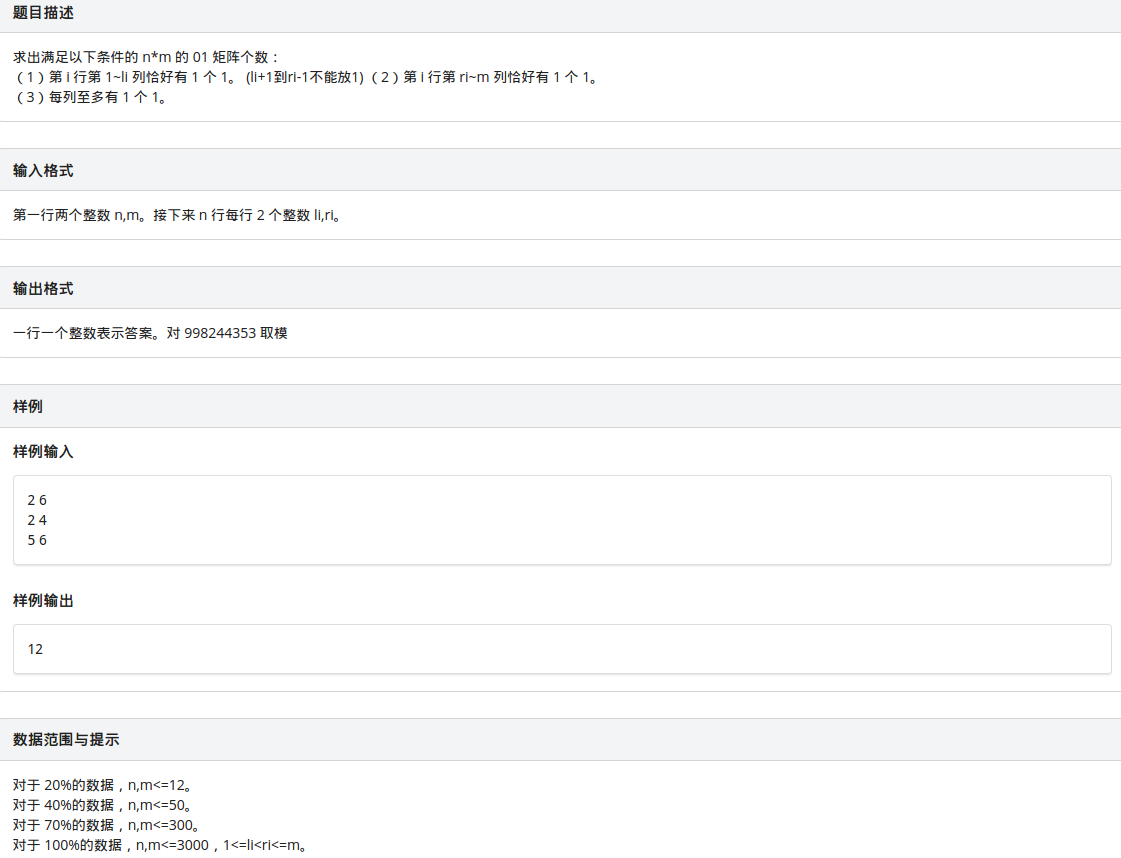
这个我在考场上的时候想了一个多小时，可就是没想出来，一直在捣鼓我的组合数，就没往dp上想

然后喜提0蛋一个；；；；；；

虽然我觉得我的思路还是没有问题滴但他就是错了

正解是dp诶

我们从左往右转移，那么我们发现左区间的方案数是可以直接通过A求得的

所以我们把重点放在右区间的转移上，

我们设dp[i][j]表示，目前到了第i列，右区间内放了j个1，左区间的方案在每一次转移的时候乘上就好了

那么我们就先考虑左区间的转移：

（等会我们先处理一个数据，这里l[i]表示左区间的终点（就是输入的l）小于等于i的个数，r[i]表示右区间的起点（就是输入的r）小于等于i的个数）

　　1、l[i]==l[i-1]那么这个时候没有新的1要放进去，所以直接由上一个状态转移  dp[i][j]+=dp[i-1][j];

　　2、l[i]>l[i-1]这个时候乘方案数了，此时一共放了j+l[i-1]个1,所以还剩下i-j-l[i-1]列可以放1,要放进去l[i]-l[i-1]个点所以乘上A(i-j-l[i-1],l[i]-l[i-1])

哎呀呀，上面那个太麻烦了，直接乘不就好了嘛，反正l[i]==l[i-1]的时候A返回的是1，，，都一样都一样啦

再考虑右区间的转移：就按照上面说的，不用分开算了

右区间一定一定从dp[i-1][j-1]转移过来因为只能加一个1嘛，这没问题吧，再乘上目前有多少个点可以用来放1，乘上A

所以dp[i][j]+=dp[i-1][j-1]*(r[i]-(j-1))*A（A同上）

因为最后一定会占满所有的矩阵，所以答案就是dp[m][n];

代码来了

#include<bits/stdc++.h>
using namespace std;
#define re register int
const int N=3005;
const int mod=998244353;
int n,m;
int f[N],b[N];
int l[N],r[N];
int jc[N],inv[N];
int dp[N][N],ans;
int ksm(int x,int y){
    int ret=1;
    while(y){
        if(y&1)ret=1ll*ret*x%mod;
        x=1ll*x*x%mod;
        y>>=1;
    }
    return ret;
}
int A(int x,int y){
    //cout<<jc[x]<<" "<<inv[x-y]<<endl;
    return 1ll*jc[x]*inv[x-y]%mod;
}
signed main(){
    scanf("%d%d",&n,&m);
    for(re i=1;i<=n;i++){
        scanf("%d%d",&f[i],&b[i]);
        l[f[i]]++;
        r[b[i]]++;
    }
    dp[0][0]=1;jc[0]=1;
    for(re i=1;i<=m;i++){
        l[i]+=l[i-1];
        r[i]+=r[i-1];
        jc[i]=1ll*jc[i-1]*i%mod;
    }
    inv[0]=1;inv[m]=ksm(jc[m],mod-2);
    //cout<<inv[m]<<endl;
    for(re i=m-1;i>=1;i--){
        inv[i]=1ll*inv[i+1]*(i+1)%mod;
    }
    for(re i=1;i<=m;i++){
        for(re j=0;j<=r[i];j++){
            //cout<<dp[i][j]<<endl;
            if(l[i]==l[i-1])dp[i][j]=(1ll*dp[i][j]+dp[i-1][j])%mod;
            else dp[i][j]=1ll*dp[i-1][j]*A(i-j-l[i-1],l[i]-l[i-1])%mod;
            if(j) dp[i][j]=(dp[i][j]+1ll*dp[i-1][j-1]*(r[i]-(j-1))%mod*A(i-j-l[i-1],l[i]-l[i-1])%mod)%mod;
        }
    }
    printf("%d",dp[m][n]);
}

T2

（心情愉悦，粘张图片）

所以T3 big

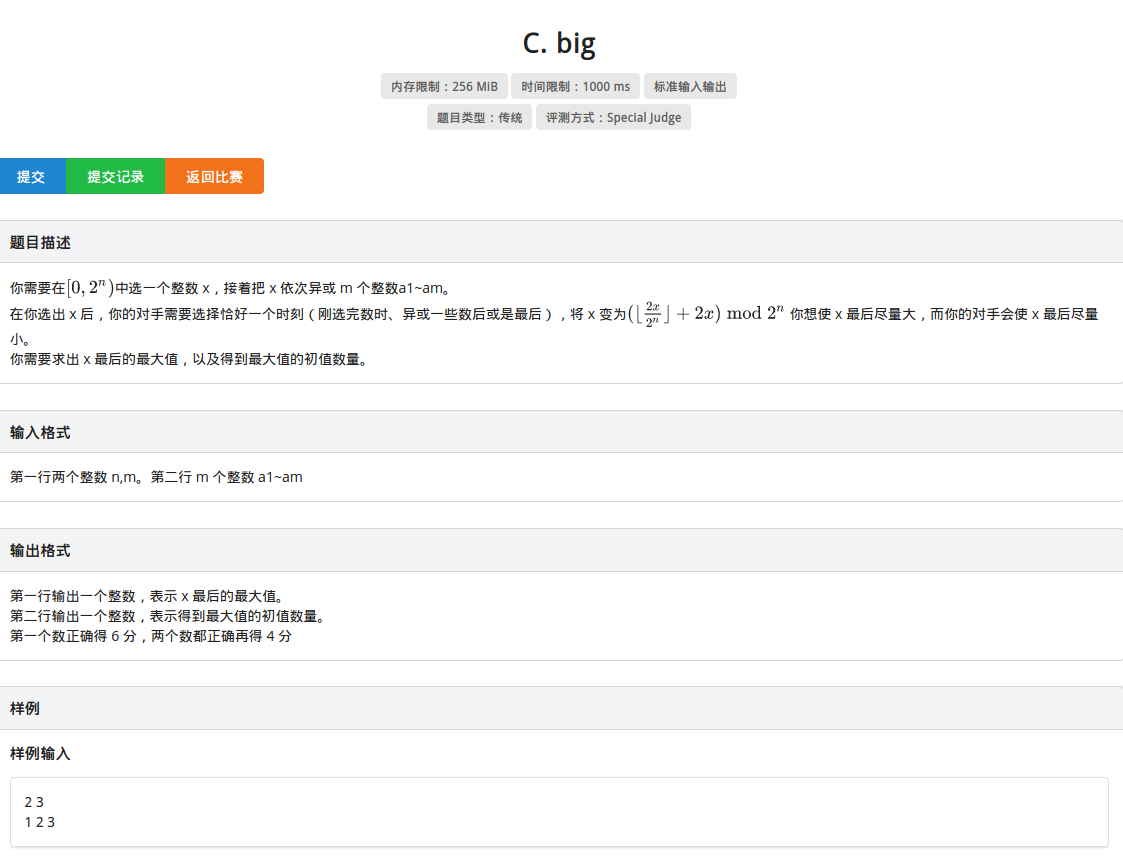
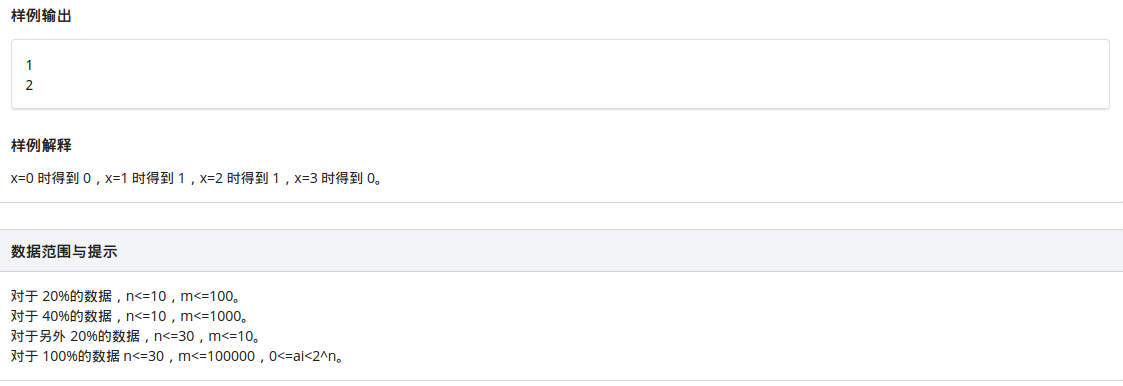
那么这个题我暴力拿到了40pts，下面是暴力代码，分别求取前缀和，然后枚举

#include<bits/stdc++.h>
using namespace std;
#define re register int
const int N=1e5+10;
int n,m;
int a[N],fro[N];
int maxn,ans,sum;
signed main(){
    scanf("%d%d",&n,&m);
    for(re i=1;i<=m;i++){
        scanf("%d",&a[i]);
        fro[i]=fro[i-1]^a[i];
    }
    for(re i=0;i<(1<<n);i++){
        int tmp;maxn=(1<<n);
        for(re j=0;j<=m;j++){
            tmp=i;
            tmp^=fro[j];
            tmp=(2*tmp/(1<<n)+2*tmp)%(1<<n);
            tmp^=fro[m]^fro[j];
            if(tmp<maxn)maxn=tmp;
        }
        if(maxn==ans)sum++;
        if(maxn>ans)ans=maxn,sum=1;
    }
    printf("%d\n%d",ans,sum);
}

全部都是TLE啊

然后正解其实是trie树

你发现他给你的那一长串，就是把x循环左移

就是1100000变成1000001,就是左移一位，然后最高位的放到最低位去，循环节就是n

然后左移的操作就成为一个分界点

可以发现如果将一个数左移一下，就相当于把他自己和那些要异或的数都左移以为

然后我们枚举每个分界点，的到了一个数组存的就是可以通过一步异或得到答案的数组

把它们放到trie树上

然后如果有一位既能取到0,也能取到1，那这一位就是一个无效位，不会对答案作出任何贡献，因为无论你拿出来的数是啥我总能把这一位变成0

所以这样就可以统计最大值和数目了

#include<bits/stdc++.h>
using namespace std;
#define re register int
const int N=100005;
int n,m;
int a[N],fro[N],beh[N];
int b[N];
struct trie{
    int v,son[2];
}tr[N*50];
int seg;
int an;
long long su;
void ins(int x){
    int u=0;
    for(re i=n-1;i>=0;i--){
        int tmp=1&(x>>i);
        //cout<<tmp<<" ";
        if(!tr[u].son[tmp])
            tr[u].son[tmp]=++seg;
        u=tr[u].son[tmp];
    }
    //cout<<endl;
}
void dfs(int x,int dep,int ans,long long sum){
    dep--;
    if(dep==-1){
        if(an<ans)an=ans,su=1;
        else if(an==ans)su++;
    }
    //cout<<x<<" "<<dep<<" "<<tr[x].son[0]<<" "<<tr[x].son[1]<<endl;
    if(!tr[x].son[0]&&!tr[x].son[1])return ;
    if(!tr[x].son[0]||!tr[x].son[1]){
        ans+=(1<<dep);
        if(tr[x].son[0])dfs(tr[x].son[0],dep,ans,sum);
        else dfs(tr[x].son[1],dep,ans,sum);
        return ;
    }
    dfs(tr[x].son[0],dep,ans,sum);
    dfs(tr[x].son[1],dep,ans,sum);
}
signed main(){
    scanf("%d%d",&n,&m);
    for(re i=1;i<=m;i++){
        scanf("%d",&a[i]);
        fro[i]=fro[i-1]^a[i];
    }
    for(re i=1;i<=m;i++){
        int t=a[i]>>(n-1);
        a[i]=a[i]<<1;
        a[i]|=t;
        b[i]=b[i-1]^a[i];
    }
    for(re i=0;i<=m;i++){
        b[i]^=fro[m]^fro[i];
        //cout<<b[i]<<endl;
        ins(b[i]);
    }
    dfs(0,n,0,1);
    printf("%d\n%lld",an,su);
}

T3

这么看的话，这个题也不算难

T4   所驼门王的宝藏

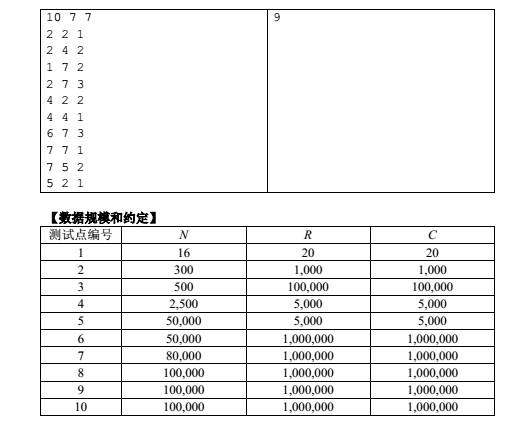
说实话这题真水，水暴了

就一个tarjan缩点

+临接表+map+记忆化搜索

#include<bits/stdc++.h>
using namespace std;
#define re register int
#define pa pair<int,int>
const int N=2000100;
int n,r,c;
struct node{
    int x,y,typ;
}mea[N];
struct edge{
    int nxt,id;
}xe[N*2],ye[N*2];
int hrp,xea[N],yea[N];
map<pa,int> zym;
int zx[10]={0,-1,-1,-1,0,0,1,1,1};
int zy[10]={0,-1,0,1,-1,1,-1,0,1};
int to[N*2],nxt[N*2],head[N],rp;
void add_edg(int x,int y){
    to[++rp]=y;
    nxt[rp]=head[x];
    head[x]=rp;
}
int dfn[N],low[N],cnt;
int pos[N],val[N],col;
int du[N],dp[N];
stack<int> q;
void dfs(int x){
    dfn[x]=low[x]=++cnt;
    q.push(x);
    for(re i=head[x];i;i=nxt[i]){
        int y=to[i];
        if(!dfn[y]){
            dfs(y);
            low[x]=min(low[x],low[y]);
        }
        else if(!pos[y]){
            low[x]=min(low[x],low[y]);
        }
    }
    if(dfn[x]==low[x]){
        pos[x]=++col;
        val[col]++;
        while(x!=q.top()&&!q.empty()){
            int y=q.top();//cout<<y<<" ";
            q.pop();
            pos[y]=col;
            val[col]++;
        }
        q.pop();
    }
}
int t_[N*2],n_[N*2],h_[N*2],r_;
void add_ed(int x,int y){
    t_[++r_]=y;
    n_[r_]=h_[x];
    h_[x]=r_;
}
int vis[N],ans;
void dfs_(int x){
    if(dp[x]>val[x])return ;
    dp[x]=val[x];
    for(re i=h_[x];i;i=n_[i]){
        int y=t_[i];
        dfs_(y);
        dp[x]=max(dp[x],dp[y]+val[x]);
    }
}
signed main(){
    scanf("%d%d%d",&n,&r,&c);
    for(re i=1;i<=n;i++){
        scanf("%d%d%d",&mea[i].x,&mea[i].y,&mea[i].typ);
        xe[++hrp].id=i;xe[hrp].nxt=xea[mea[i].x];xea[mea[i].x]=hrp;
        ye[hrp].id=i;ye[hrp].nxt=yea[mea[i].y];yea[mea[i].y]=hrp;
        pa a=(pa){mea[i].x,mea[i].y};zym[a]=i;
    }
    for(re i=1;i<=n;i++){
        int x=mea[i].x,y=mea[i].y,typ=mea[i].typ;
        if(typ==1){
            for(re j=xea[x];j;j=xe[j].nxt)
                if(i!=xe[j].id)add_edg(i,xe[j].id);
        }
        else if(typ==2){
            for(re j=yea[y];j;j=ye[j].nxt)
                if(i!=ye[j].id)add_edg(i,ye[j].id);
        }
        else{
            for(re j=1;j<=8;j++){
                pa a=(pa){x+zx[j],y+zy[j]};
                if(zym[a])add_edg(i,zym[a]);
            }
        }
    }
    for(re i=1;i<=n;i++)
        if(!dfn[i])dfs(i);
    for(re i=1;i<=n;i++){
        for(re j=head[i];j;j=nxt[j])
            if(pos[i]!=pos[to[j]])
                add_ed(pos[i],pos[to[j]]),du[pos[to[j]]]++;//cout<<pos[to[j]]<<" ";
    }
    for(re i=col;i>=1;i--){
        if(du[i]==0){
            dfs_(i);
            ans=max(ans,dp[i]);
        }
    }
    printf("%d",ans);
}

T3

完结撒花！！！！！