JQuery的链式编程，隐式迭代是啥意思？

链式编程

1.好处

“一句话，链式编程可以省去很多重复的代码。”

这话什么意思呢？举个例子。

/*设置obj对象的两个属性*/

//普通做法是这样的

obj.name = '小明';

obj.age =  155；

//链式编程是这样的。

obj.name('小明').age(15);

2.注意

链式编程注意：

$(‘div’).html(‘设置值’).val(‘设置值’);这样是可以的。

但是$(‘div’).html().text()这样是不对的，因为获取值时返回的是获取的字符串而不是对象本身所以不能链式编程。

3.断链了咋整

链式编程的时候一定要注意在什么时候“破坏”了链，当前对象的传递，如果传递被破坏，则继续链式编程会有意想不到的结果！nextAll(),prevAll(),sibilings()

如何解决：调用end()方法。（返回链 被破坏前的对象。）

隐式迭代

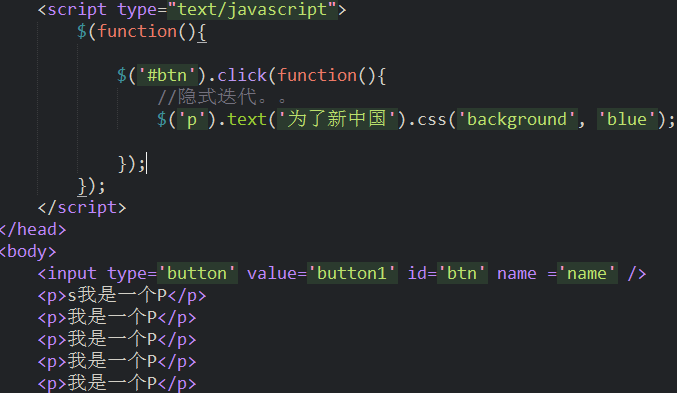
上面例子中

$('#btn').click(function(){

//隐式迭代。。

$('p').text('为了新中国').css('background', 'blue');

});

获取元素P，在传统的dom写法中getElementsByTagName 发现没有方法名Elements 是复数形式。

也就是说获得的应该是一个集合。

我们知道设置集合中元素的属性，那必须的迭代啊。（就是遍历一下啊）

但是Jquery中不需要遍历可以直接设置。  为啥呢？ 这就是隐式迭代呗。