SPSS 分布类型的检验

假设检验的标准步骤：

1、建立假设：根据问题的需要提出原假设H₀，以及其对立面备择假设H₁。

2、确立检验水准：即设立小概率事件的界值α。

3、进行试验：得到用于统计分析的样本，以该试验的结果作为假设检验的根据。

4、选定检验方法，计算检验统计量。

5、确定P值。

原假设也称为零假设，备择假设也称为对立假设。对立假设就是对立于原假设，备择假设的意思是，一旦你决定不采纳原假设，则这假设可备你选择。

根据统计学观点，接受原假设和否定原假设，二者的意义并非对等。接受原假设只是意味着，按所获数据来看，并无足够的根据认为原假设不对，而不是说，从所获数据证明了原假设是对的，因此，问题多少仍处于未决的局面。反之，否定原假设则意味着，按所获数据有充足理由（而非绝对地证明，因为数据有随机性）认为原假设不对，即有充足理由认为对立假设成立。故在一定限度内，可以说问题由了一个明确的结论。

假设检验的基本思想是统计学的“小概率反证法”原理：对于一个小概率事件而言，其对立面发生的可能性显然要大大高于这一小概率事件，可以认为小概率事件在一次试验中不应当发生。

假设检验除了分为单/双侧检验外，还可以分为参数检验和非参数检验。参数检验是已知数据的分布形式，只是不了解相应参数时的检验形式。如果数据的分布形式不了解，就必须使用非参数检验确定数据的分布形式。下面将介绍几种常用分布的假设检验。

一、正态分布的检验

正太分布的考察方法有：通过计算偏度系数和峰度系数加以考察；通过绘制直方图、PP图等图形工具来考察；也可以进行各种假设检验。最常用的就是K-S单样本检验。

K-S检验通过对两个分布之间的差异的分析，判断样本的观察结果是否来自制定分布的总体。计算P值的公式比较复杂，可不必深究。

分析者可以直接使用K-S检验对样本数据进行正态分布的检验，但值得推荐的第一步是对样本数据进行图形描述，图形可以给分析者一个直观的印象：该数据可能服从什么样的分布类型。

文彤老师的书中对消费者信心指数进行了K-S检验，大致步骤是“分析”——“非参数检验”——“单样本”……，当然首先要选择个案：数据——选择个案——如果条件满足time=200704。然后再进行K-S检验，我的SPSS可能由于版本问题，运行时出现“停止执行该命令”。但是使用旧对话框是可以的，分析——非参数检验——旧对话框——1样本K-S。

文彤老师对检验结果的批注很值得一读：既然此处拒绝了正态分布假设，那么分析时还可以使用如t检验等对变量分布有要求的方法吗？事实上，K-S检验从实用性角度来说远不如图形工具，因为在样本量少的时候它不够敏感，而样本量大时又总是过于敏感。本例就属于敏感过头的情况，实际上读者们只需要绘制P-P图就可以发现，该数据实际上是基本符合正态分布趋势的，进行后续数据分析时遵循正态分布的分析思路应当不会有任何问题。

二、二项分布检验

二项分布检验是对二分类变量的拟合优度检验，用于考察每个类别中观察值的频数与特定分布下的预期频数间是否存在统计学差异。例子详见参考资料1。

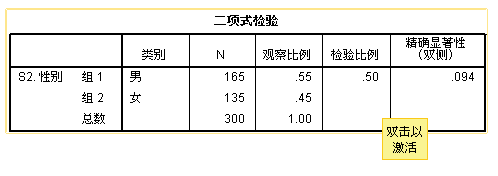
三、游程检验

游程检验是对二分变量的随机检验，判断观察值的顺序是否为随机的。

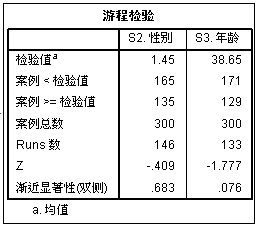
文彤老师提醒： 在对连续性变量进行游程检验时，采用不同的分割点，就可能得到截然不同的分析结果，因此在实际分析中，应当尽可能多取几个在专业背景上有实际意义的数值作为分割点，比较其游程检验的结果，以得到对序列随机性更为稳健和客观的结论。

参考资料：

1. 张文彤. 《SPSS统计分析基础教程》

2. 陈希孺. 《统计学漫话》