Gnome桌面的下拉式终端： Guake

什么是Guake？

Guake是应用于Gnome环境的下拉式终端。主要由Python编写，使用了一些C，它以GPL2+许可证发布，适用于Linux以及类似的系统。Guake的灵感来源于电脑游戏Quake（雷神之锤）中的终端，Quake的终端能通过按下特定按键（默认为F12）从屏幕上滑下来，并在按下同样的键后滑上去。

值得注意的是，Guake并不是第一个这样的应用。Yakuake（Yet Another Kuake）是一个运行于KDE的终端模拟器，Tilda是一个用GTK+写成的终端模拟器。它们的灵感都来自于雷神之锤那上下滑动的终端。

Guake的功能

1. 轻量级
2. 简单而优雅
3. 功能众多
4. 强大
5. 美观
6. 将终端平滑地集成于GUI中
7. 在按下预定义的键后出现/消失
8. 支持热键、标签、透明化背景，这使得它适合所有Gnome用户
9. 可配置各种方面
10. 包括许多颜色的调色板
11. 设定透明度的快捷方式
12. 通过Guake配置，可在启动时运行一个脚本
13. 可以在多个显示器上运行

在Linux中安装Guake终端

Guake可以在许多的发行版中通过添加额外的仓库来安装。这里我们将在Debian、Ubuntu、Linux Mint和Fedora下安装Guake。

首先从仓库获取最新的软件包列表，并从默认的仓库安装Guake，如下所示：

---------------- 在 Debian, Ubuntu 和 Linux Mint 上 ----------------
$ sudo apt-get update
$ apt-get install guake

---------------- 在 Fedora 19 及其以后版本 ----------------
# yum update
# yum install guake

安装后，可以从另一个终端中启动Guake：

$ guake

在启动它后，便可以在Gnome桌面中使用F12（默认配置）来拉下、收回终端。

看起来非常漂亮，尤其是透明背景。滑下来...滑上去...滑下来...滑上去...执行命令，打开另一个标签，执行命令，滑上去...滑下来...

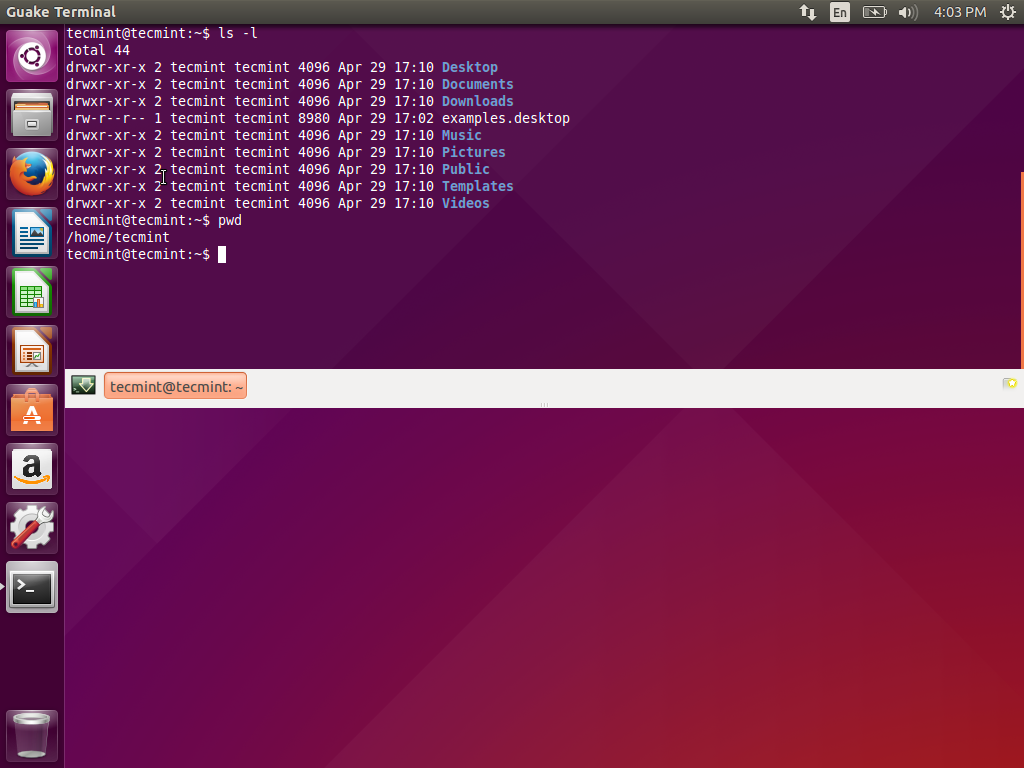
如果您的壁纸或活动窗口的颜色和Guake的颜色有些不搭。您可以改变您的壁纸，减少透明度或者改变Guake的颜色。

下一步便是进入Guake的配置，根据每个人的需求修改设置。可以通过应用菜单或者下面的命令来运行Guake的配置。

$ guake --preferences

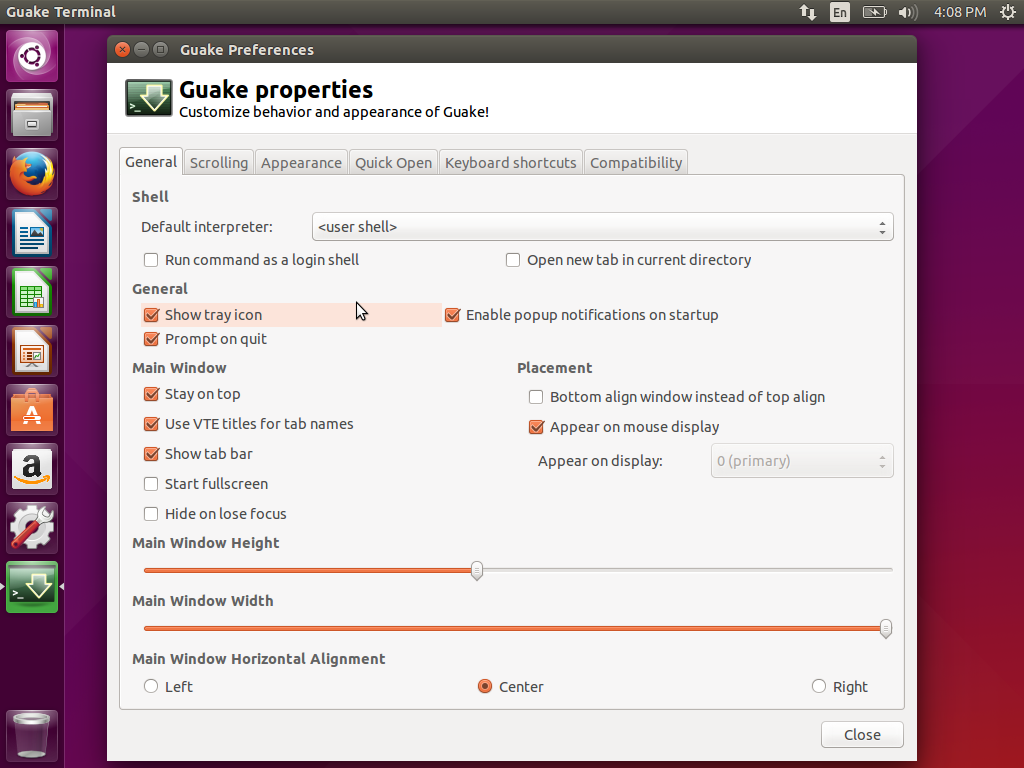
设置滚动

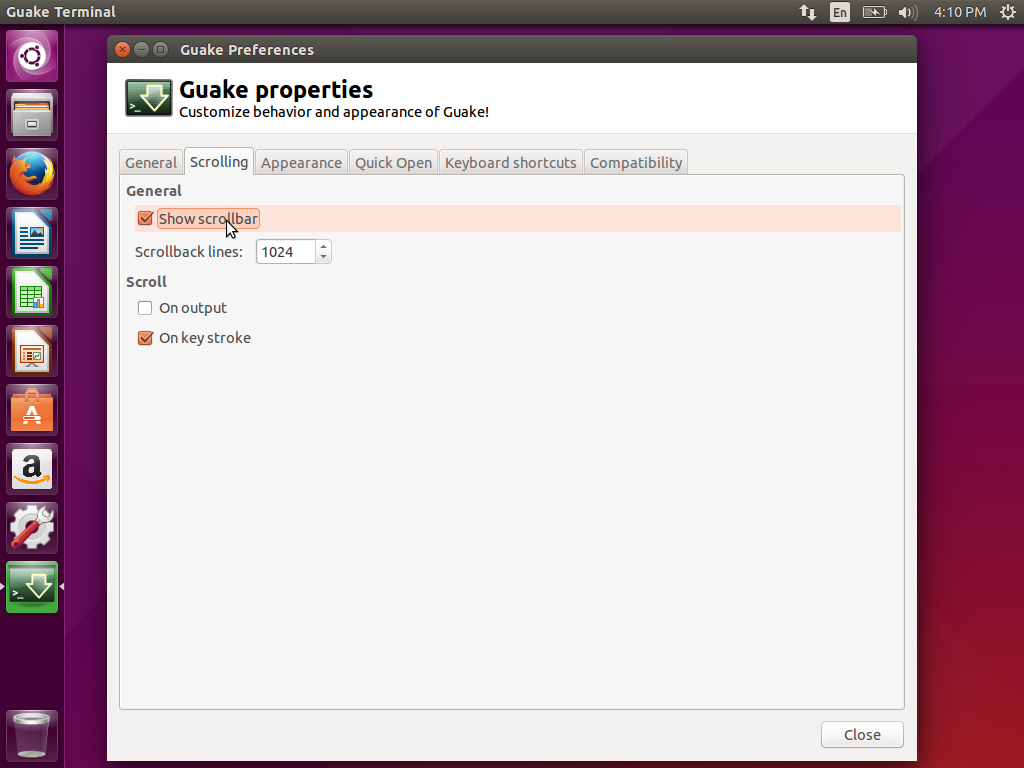
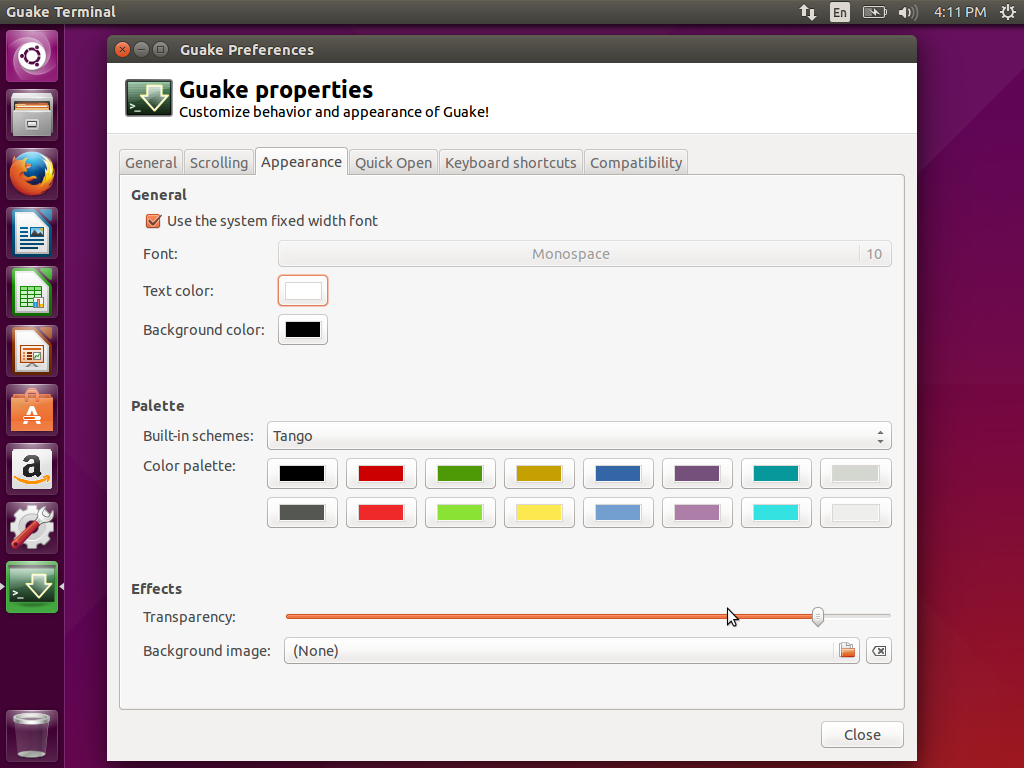
外观设置 - 在这里您可以修改文字颜色和背景色以及透明度。

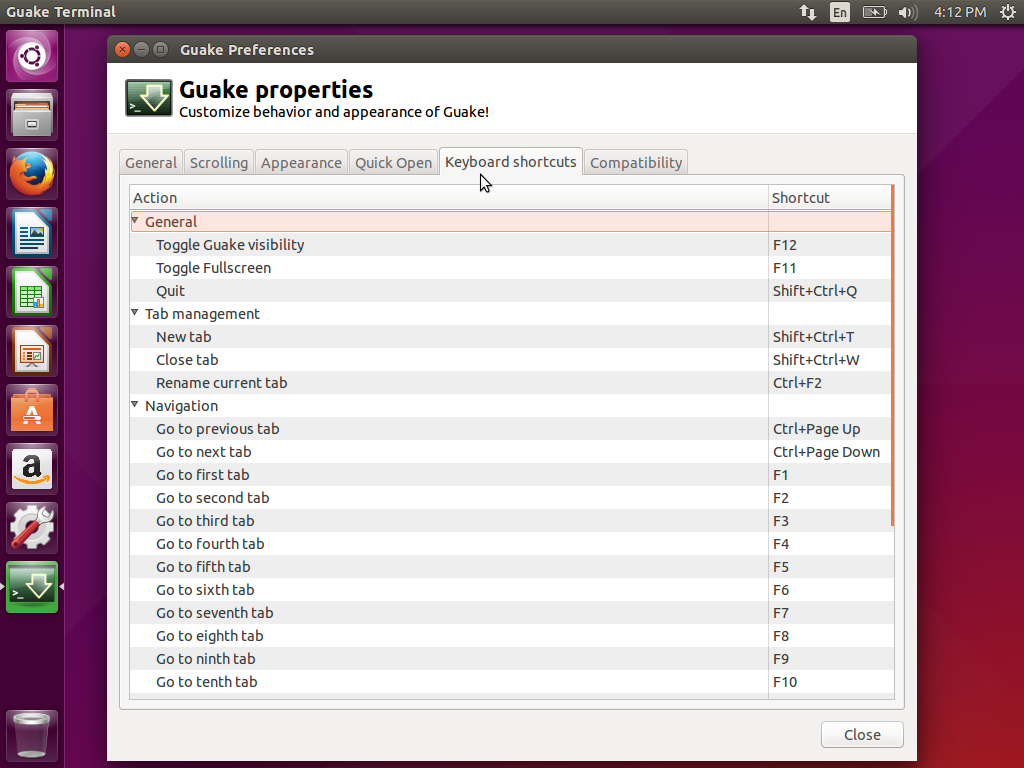
键盘快捷键 - 在这里您可以修改Guake显示的开关快捷键。

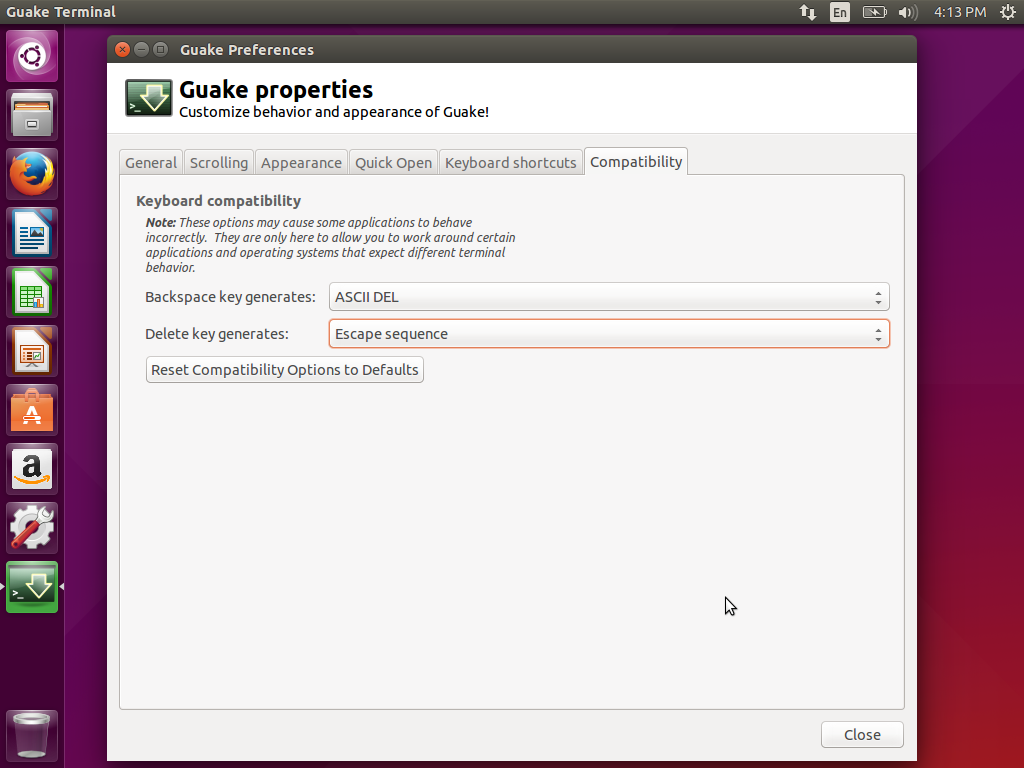
兼容性设置 - 基本上不必设置它。

结论

这个项目即不是太年轻也不是太古老，因此它已经达到了一定的成熟度，足够可靠，可以开箱即用。像我这样需要在GUI和终端间频繁切换的人来说，Guake是一个福利。我不需要管理一个多余的窗口，频繁的打开和关闭，使用tab在大量打开的应用程序中寻找终端或切换到不同的工作区来管理终端，现在我需要的只有F12。

我认为对任何同时使用GUI和终端的Linux用户来说，Guake都是必须的工具。同样的，我会向任何想要在系统中结合使用GUI和终端的人推荐它，因为它既平滑又没有任何障碍。

上面就是我要说的全部了。如果在安装和使用时有任何问题，请告诉我，我们会帮助您。也请您告诉我您使用Guake的经验。在下面的评论区反馈您宝贵的经验。点赞和分享以帮助我们宣传。

免费提供最新Linux技术教程书籍，为开源技术爱好者努力做得更多更好：https://www.linuxprobe.com/