HDU 4828 逆元+catalan数

Grids

Time Limit: 10000/5000 MS (Java/Others)    Memory Limit: 65535/65535 K (Java/Others)
Total Submission(s): 953    Accepted Submission(s): 418

Problem Description

　　度度熊最近很喜欢玩游戏。这一天他在纸上画了一个2行N列的长方形格子。他想把1到2N这些数依次放进去，但是为了使格子看起来优美，他想找到使每行每列都递增的方案。不过画了很久，他发现方案数实在是太多了。度度熊想知道，有多少种放数字的方法能满足上面的条件？

 

Input

　　第一行为数据组数T(1<=T<=100000)。
　　然后T行，每行为一个数N(1<=N<=1000000)表示长方形的大小。

 

Output

　　对于每组数据，输出符合题意的方案数。由于数字可能非常大，你只需要把最后的结果对1000000007取模即可。

 

Sample Input

2
1
3

 

Sample Output

Case #1:
1
Case #2:
5

Hint

对于第二组样例，共5种方案，具体方案为：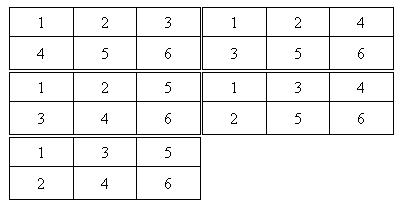

 

Source

2014年百度之星程序设计大赛 - 初赛（第一轮）

 暴力找出前几项可知  1,2,5,14,42、、、容易看出是卡特兰数，递推公式   f(n+1)=(4*n-6)/n*f(n)  |  f(1)=f(2)=1   n>=2;

由于数很大需要取模用到了逆元，这里上界100w所以用了打表法，唯一要注意的一点就是，在处理4-6/n时，由于减法可能出现负数

我们写成 ( 4-6*inv[n]+mod )的形式但是这样还是会出现负数，因为6*inv[n]可能大于mod，这里只要多加几个mod即可解决

 #include<bits/stdc++.h>
 using namespace std;
 #define LL long long
 const LL mod=1e9+;
 LL inv[]={,};
 LL cat[]={,,};
 void init()
 {
     for(int i=;i<=;++i)
         inv[i]=(mod-mod/i)*inv[mod%i]%mod;
     for(int i=;i<=;++i)
         cat[i]=cat[i-]*((+*mod-*inv[i-])%mod)%mod;
 }
 int main()
 {
     int t,k=,i,n;
     scanf("%d",&t);
     init();
     for(i=;i<=t;++i){
         scanf("%d",&n);
         printf("Case #%d:\n%lld\n",i,cat[n+]);
     }
     return ;
 }