PHP扩展--taint检测隐藏漏洞

简介

Taint 可以用来检测隐藏的XSS code, SQL注入, Shell注入等漏洞, 并且这些漏洞如果要用静态分析工具去排查, 将会非常困难, 比如对于如下的例子:

<?php
   echo $_GET["name"];
?>

对于请求:

http://localhost/?name=222

静态分析工具, 往往无能为力, 而Taint却可以准确无误的爆出这类型问题.

Warning: Main::test() [function.echo]: Attempt to echo a string that might be tainted in

taint安装

wget http://pecl.php.net/get/taint-1.2.2.tgz
tar zxvf taint-1.2.2.tgz
cd taint-1.2.2
/usr/local/php/bin/phpize
./configure --with-php-config=/usr/local/php/bin/php-config
make && make install

配置php.ini

[taint]
extension=taint.so
taint.enable=1
taint.error_level=E_WARNING

运行结果

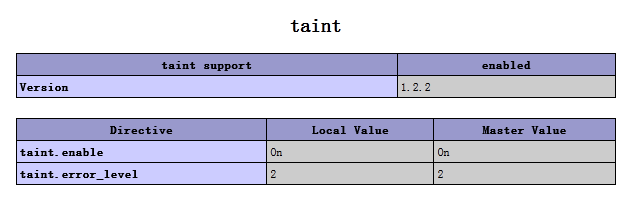
php -i | grep taint
taint
taint support => enabled
taint.enable => On => On
taint.error_level => 2 => 2

###附录

A. 验证的字符串

所有来自GET,GET,_POST, $_COOKIE的变量, 都被认为是Tainted String

B. taint检测的函数/语句列表, 当这些函数使用tainted string参数的时候, taint会给出警告:

1. 输出函数/语句系列

    echo
    print
    printf
    file_put_contents

2. 文件系统函数

    fopen
    opendir
    basename
    dirname
    file
    pathinfo

3. 数据库系列函数/方法

    mysql_query
    mysqli_query
    sqlite_query
    sqlite_single_query
    oci_parse
    Mysqli::query
    SqliteDataBase::query
    SqliteDataBase::SingleQuery
    PDO::query
    PDO::prepare

4. 命令行系列

    system
    exec
    proc_open
    passthru
    shell_exec

5. 语法结构

    eval
    include(_once)
    require(_once)

C. 消除tainted信息的函数, 调用这些函数以后, tainted string就会变成合法的string:

escapeshellcmd
htmlspecialchars
escapeshellcmd
addcslashes
addslashes
mysqli_escape_string
mysql_real_escape_string
mysql_escape_string
sqlite_escape_string
PDO::quote
Mysqli::escape_string
Mysql::real_escape_string

D. 调用中保持tainted信息的函数/语句, 调用这些函数/语句时, 如果输入是tainted string, 则输出也为tainted string:

=
.
"{$var}
.=
strval
explode
implode
sprintf
vsprintf
trim
rtrim
ltrim

来自为知笔记(Wiz)