[机器学习]-Adaboost提升算法从原理到实践

1.基本思想：

综合某些专家的判断，往往要比一个专家单独的判断要好。在”强可学习”和”弱可学习”的概念上来说就是我们通过对多个弱可学习的算法进行”组合提升或者说是强化”得到一个性能赶超强可学习算法的算法。如何地这些弱算法进行提升是关键！AdaBoost算法是其中的一个代表。

2.分类算法提升的思路：

1.找到一个弱分类器，分类器简单，快捷，易操作(如果它本身就很复杂，而且效果还不错，那么进行提升无疑是锦上添花，增加复杂度，甚至上性能并没有得到提升，具体情况具体而论)。

2.迭代寻找N个最优的分类器(最优的分类器，就是说这N个分类器分别是每一轮迭代中分类误差最小的分类器，并且这N个分类器组合之后是分类效果最优的。)。

在迭代求解最优的过程中我们需要不断地修改数据的权重(AdaBoost中是每一轮迭代得到一个分类结果与正确分类作比较，修改那些错误分类数据的权重，减小正确分类数据的权重 ),后一个分类器根据前一个分类器的结果修改权重在进行分类，因此可以看出，迭代的过程中分类器的效果越来越好，所以需要给每个分类器赋予不同的权重。最终我们得到了N个分类器和每个分类器的权重，那么最终的分类器也得到了。

3.算法流程：(数据默认：M*N,M行N列，M条数据，N维 )

输入：训练数据集,：弱学习算法(x_i表示数据i[数据i是个N列/维的],y_i表示数据的分类为y_i,Y={-1,1}表示x_i在某种规则约束下的分类可能为-1或+1)

输出：最终分类器G(x)

　　 1)初始化训练数据的权值分布(初始化的时候每一条数据权重均等)

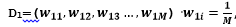　　　　 ,M表示数据的个数，i=1,2,3…M　

　　 2)j=1,2,3,…,J(表示迭代的次数/或者最终分类器的个数,取决于是否能够使分类误差为0)

　　　　　a)使用具有权值分布D_j的训练数据集学习，得到基本的分类器

　　　　　　　　G_j(x):X->{-1,+1}

　　　　　b)计算G_j(x)在训练集上的分类误差率

　　　　　　　 

　　　　　　　  求的是分错类别的数据的权重值和,表示第i个数据的权重D_j[i]

　　　　  c)计算G_j(x)第j个分类器的系数(权重),ln表示以E为底的自然对数跟e_j没什么关系,e_j表示的是分类错误率。

　　　　 　

　　　　　d)更新训练数据集的权重D_j+1,数据集的权重是根据上一次权重进行更新的， i=1,2,3…M(x_i表示第i条数据)

　　　　　　　

　　　　    　

　　　　　 　 　

　　　　　　　　Z是规范化因子，他表示所有数据权重之和，它使D_j+1成为一个概率分布。

　　　　3)构建基本分类器的线性组合

　　　　　　

　　　　　　得到最终的分类器：

　　　　     

4.用一组数据来具体解说一下Adaboost的实现过程:

   Data：5*2

　

原始类别：

　

   1.初始化数据权重D1=（1/5,1/5,1/5,1/5,1/5）,五条数据所以是5列，w=1/m

  2.分类器

　　　　　　

　　  通过计算得到误差率最小时V的值，但是最小误差率是由分类结果G（x）得到的，所以这个V值我们只有通过穷举得到。

　　 1).按第一维度来分类：　　　

　　　　我们找到第一维所有数据的极值（min=1,max=2）,我们从最小的数据1开始，每次增加0.5，即V=min+0.5*n,n表示次数。

　　　　当v=1+0.5*1=1.5时，

　　　　分类结果G(x):

　　　　　　G(x)=[1<1.5->1,2>1.5->-1,1.3<1.5->1,1<1.5->1,2>1.5->-1]

　　　　　　G(x)=[1,-1,1,1,-1]

      　误差率为e₁:

            e₁=sum(D[G(xi)!=yi])误分类点的权重和

我们来比较一下分类器的分类结果和原始类别就知道那些分错了：

　　　　　　 G(x)=[1,-1,1,1,-1]

　　　　　　 Lables=[1,1,-1,-1,1]

对比一下可以发现第2，3，4,5都分错了。

e₁=D[2]+D[3]+D[4]+D[5]=0.8

            交换一下符号：即

　　　　 　　

　　　  分类结果G(x):

　　　　　　 G(x)=[1<1.5->-1,2>1.5->1,1.3<1.5->-1,1<1.5->-1,2>1.5->1]

　　　　　　 G(x)=[-1,1,-1,-1,1]

        误差率为e₁:

　　　　　　 G(x)=[-1,1,-1,-1,1]

　　　　　   Lables=[1,1,-1,-1,1]

对比一下可以发现第1个错了。

　e₁=D[1]=0.2

        分类器权重alpha:

            Alpha = 0.5*ln((1-0.2)/0.2)

        更新数据权重D：

　　　　     sum(D1)=1

            D2=((D1[1]*e^(-alpha*-1))/sum(D1), (D1[1]*e^(-alpha*1))/1,..)

   　　     e的系数最后的+-1取决于是否正确分类，分正确了就是1，分错误了就是-1，前面公式中也有写到。

　 　 这里的计算公式是统计学习方法中的，跟机器学习实战中的D的计算有一点出入，在机器学习实战中D是这么计算的：

            D2= D1[1]*e^(-alpha*-1)

            D2=D2/sum(D2)

            但是就结果而言，好像影响不大，只是对这个加权误差有影响。

　 我们得到两个分类器：

　 　　  

　  　      

　　　当v=1+0.5*2=1.5时，

　　重复以上步骤得到两个分类器。

　　　当v=1+0.5*s时，一共寻找了2s次

　　 当我们从最小值找分类阈值直到最大值时，我们得到了2s个分类器，s表示寻找的次数。我们记录效果最好的分类器即分类误差最小的分类器。那么我们在一个维度上的寻找就完成了。

     2).接下来在第二个维度上寻找，同样得到2s个分类器

　　   。。。

　   3).直到第N维,总共得到N*2s个分类器，最终在这么多分类器找到一个最优的分类器。一次迭代完成。

 3.接下来将上面这个过程重复J次(J表示迭代次数，如果h次(h<J)就得到了误差为0的分类器那么提前结束迭代。)

　　按所给数据，迭代三次就能够找到误差为零的分类器

看到这里应该对整个过程有了一个了解，对于数据权重D和分类器的权重alpha，以及分类误差率e的计算都有了一个了解，看一下代码：

源码：（源码是按照《机器学习实战》来写的，因为个人对于python不太熟，机器学习实战中的代码运用矩阵来做很多公式中的乘法，有很大的技巧性，可能开始看的时候没法理解这样做，需要和理论结合，理论则是是来自《统计学习方法》）

 # -*- coding:utf-8 -*-
 # Filename: AdaBoost.py
 # Author：Ljcx

 """
     AdaBoost提升算法:(自适应boosting)
         优点：泛化错误率低，易编码，可以应用在大部分分类器上，无参数调整
         缺点：对离群点敏感

     bagging:自举汇聚法(bootstrap aggregating)
         基于数据随机重抽样的分类器构建方法
         原始数据集中重新选择S次得到S个新数据集，将磨沟算法分别作用于这个数据集,
         最后进行投票，选择投票最多的类别作为分类类别

     boosting:类似于bagging,多个分类器类型都是相同的

         boosting是关注那些已有分类器错分的数据来获得新的分类器，
         bagging则是根据已训练的分类器的性能来训练的。

         boosting分类器权重不相等，权重对应与上一轮迭代成功度
         bagging分类器权重相等
 """
 from numpy import*

 class Adaboosting(object):

     def loadSimpData(self):
         datMat = matrix(
             [[1., 2.1],
              [2., 1.1],
              [1.3, 1.],
              [1., 1.],
              [2., 1.]])
         classLabels = [1.0, 1.0, -1.0, -1.0, 1.0]
         return datMat, classLabels

     def stumpClassify(self, datMat, dimen, threshVal, threshIneq):
         """
         通过阈值比较进行分类
             dataMat:数据矩阵
             dimen:表示列下标
             threshVal:阈值
             threshIneq:不等号  lt, gt
         只是简单的将数据分为两类-1，1，初始化了一个全1的矩阵，我们判断一下阈值第i列小于/大于阈值的就为-1，(因为我们并不清楚这个划分标准，所以要大于小于都试一次)

         每一个维度的所有数据跟阈值比较，就相当于找到一个点划分所有数据。

         """
         # print "-----data-----"
         # print datMat
         retArr = ones((shape(datMat)[0], 1))  # m(数据量)行，1列，列向量
         if threshIneq == 'lt':
             retArr[datMat[:, dimen] <= threshVal] = -1.0  # 小于阈值的列都为-1
         else:
             retArr[datMat[:, dimen] > threshVal] = -1.0  # 大于阈值的列都为-1
         # print "---------retArr------------"
         # print retArr
         return retArr

     def buildStump(self, dataArr, classLables, D):
         """
         单层决策树生成函数
         """
         dataMatrix = mat(dataArr)
         lableMat = mat(classLables).T
         m, n = shape(dataMatrix)
         numSteps = 10.0  # 步数，影响的是迭代次数，步长
         bestStump = {}  # 存储分类器的信息
         bestClassEst = mat(zeros((m, 1)))  # 最好的分类器
         minError = inf  # 迭代寻找最小错误率
         for i in range(n):
             # 求出每一列数据的最大最小值计算步长
             rangeMin = dataMatrix[:, i].min()
             rangeMax = dataMatrix[:, i].max()
             stepSize = (rangeMax - rangeMin) / numSteps
             # j唯一的作用用步数去生成阈值，从最小值大最大值都与数据比较一边了一遍
             for j in range(-1, int(numSteps) + 1):
                 threshVal = rangeMin + float(j) * stepSize  # 阈值
                 for inequal in ['lt', 'gt']:
                     predictedVals = self.stumpClassify(
                         dataMatrix, i, threshVal, inequal)
                     errArr = mat(ones((m, 1)))
                     errArr[predictedVals == lableMat] = 0  # 为1的 表示i分错的
                     weightedError = D.T * errArr  # 分错的个数*权重(开始权重=1/M行)
                     # print "split: dim %d, thresh %.2f, thresh ineqal:\
 #%s,the weighted error is %.3f" % (i, threshVal, inequal, weightedError)
                     if weightedError < minError:  # 寻找最小的加权错误率然后保存当前的信息
                         minError = weightedError
                         bestClassEst = predictedVals.copy()  # 分类结果
                         bestStump['dim'] = i
                         bestStump['thresh'] = threshVal
                         bestStump['ineq'] = inequal
         # print bestStump
         # print minError
         # print bestClassEst  # 类别估计
         return bestStump, minError, bestClassEst

     def adaBoostingDs(self, dataArr, classLables, numIt=40):
         """
         基于单层决策树的AdaBoosting训练过程：
         """
         weakClassArr = []  # 最佳决策树数组
         m = shape(dataArr)[0]
         D = mat(ones((m, 1)) / m)
         aggClassEst = mat(zeros((m, 1)))
         for i in range(numIt):
             bestStump, minError, bestClassEst = self.buildStump(
                 dataArr, classLables, D)
             print "bestStump:", bestStump
             print "D:", D.T
             alpha = float(
                 0.5 * log((1.0 - minError) / max(minError, 1e-16)))
             bestStump['alpha'] = alpha
             weakClassArr.append(bestStump)
             print "alpha:", alpha
             print "classEst:", bestClassEst.T  # 类别估计

             expon = multiply(-1 * alpha * mat(classLables).T, bestClassEst)
             D = multiply(D, exp(expon))
             D = D / D.sum()

             aggClassEst += alpha * bestClassEst
             print "aggClassEst ；", aggClassEst.T
             # 累加错误率
             aggErrors = multiply(sign(aggClassEst) !=
                                  mat(classLables).T, ones((m, 1)))
             # 错误率平均值
             errorsRate = aggErrors.sum() / m
             print "total error:", errorsRate, "\n"
             if errorsRate == 0.0:
                 break
         print "weakClassArr:", weakClassArr
         return weakClassArr

     def adClassify(self, datToClass, classifierArr):
         """
         预测分类：
         datToClass：待分类数据
         classifierArr: 训练好的分类器数组
         """
         dataMatrix = mat(datToClass)
         m = shape(dataMatrix)[0]
         aggClassEst = mat(zeros((m, 1)))
         print
         for i in range(len(classifierArr)):  # 有多少个分类器迭代多少次
             # 调用第一个分类器进行分类
             classEst = self.stumpClassify(dataMatrix, classifierArr[i]['dim'],
                                           classifierArr[i]['thresh'],
                                           classifierArr[i]['ineq']
                                           )
             # alpha 表示每个分类器的权重，
             print classEst
             aggClassEst += classifierArr[i]['alpha'] * classEst
             print aggClassEst
         return sign(aggClassEst)

 if __name__ == "__main__":
     adaboosting = Adaboosting()
     D = mat(ones((5, 1)) / 5)
     dataMat, lableMat = adaboosting.loadSimpData()
     # 训练分类器
     classifierArr = adaboosting.adaBoostingDs(dataMat, lableMat, 40)
     # 预测数据
     result = adaboosting.adClassify([0, 0], classifierArr)
     print result

运行结果：可以看到迭代三次加权错误率为0

最后有一个对数据[0,0]的预测：weakClassArr表示保存的三个分类器的信息，我们用这个分类器对数据进行预测

三个小数对应的是三个分类器前N个分类加权分类结果累加。对应的-1，-1，-1表示三个分类器对这个数据分类是-1，最后一个表示增强分类器对这个数据的加权求和分类结果为-1