PKU 3020 Antenna Placement(拆点+最小边覆盖)(最大匹配)

题目大意：原题链接

一个矩形中，有N个城市’*’，现在这n个城市都要覆盖无线，若放置一个基站，那么它至多可以覆盖相邻的两个城市。
问至少放置多少个基站才能使得所有的城市都覆盖无线？

提示：看清楚题目，'*'是城市，'o'是空地，椭圆的天线覆盖范围要覆盖的是城市'*',而不是覆盖空地

解题思路：关键是建模构图

每两个相邻的星号连一条边，很明显这是一道求二分图的最小边覆盖问题（注意不是最小点覆盖）

那么接下来需要确认的是，究竟是求 有向二分图的最小边覆盖，还是求 无向二分图的最小路覆盖

因为有向和无向是截然不同的计算方法。

要确认是构造有向图，还是构造无向图，那么就需要先根据题意，看看构造二分图时所使用的方式，更适合构造哪一种二分图。

然后就进入了本题难点：如何构造二分图

首先要明确的是，输入的一堆“圈圈星星”可以看做是一张大地图，地图上有所有城市的坐标，但是这里有一个误区：不能简单地把城市的两个x、y坐标作为准备构造的二分图的两个顶点集。

城市才是要构造的二分图的顶点！

构造方法如下：

例如输入：

*oo

***

o*o

时，可以抽象为一个数字地图：

100

234

050

数字就是根据输入的城市次序作为该城市的编号，0代表该位置没有城市。

然后根据题目的“范围”规则，从第一个城市开始，以自身作为中心城市，向四个方向的城市进行连线（覆盖）

因此就能够得到边集：

e12   e21     e32     e43    e53

e23     e34

e35

可以看到，这些边都是有向边，但是每一条边都有与其对应的一条相反边。

即任意两个城市（顶点）之间的边是成对出现的

那么我们就可以确定下来，应该 构造无向二分图（其实无向=双向）

因为若要构造有向的二分图时，需要判断已出现的边，是很麻烦的工作

为了把有向图G构造为无向二分图，这里需要引入一个新名词“拆点”

其实就是把原有向图G的每一个顶点都”拆分（我认为复制更准确）”为2个点，分别属于所要构造的二分图的两个顶点集

例如在刚才的例子中抽出一条有向边e12举例说明：

复制顶点1和顶点2，使得1，2∈V1；  1’，2’∈V2 ，不难发现|V1|=|V2|

根据边e12和e21，得到无向二分图：

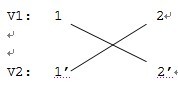
那么同理就可以得到刚才的例子的 无向二分图为：

再继而通过无向二分图，以V1的元素作为row，V2的元素作为col，构造 可达矩阵 存储到计算机

1’  2’  3’  4’  5’

1  F  T   F   F   F

2  T  F   T   F   F

3  F  T   F   T   T

4  F  F   T   F   F

5  F  F   T   F   F

接下来就是要求这个 无向二分图的最小边覆盖 了

利用公式：

无向二分图的最小边覆盖 = 顶点数 – 最大二分匹配数/2

顶点数：就是用于构造无向二分图的城市数，即进行“拆点”操作前的顶点数量

最大二分匹配数之所以要除以2，是因为进行了“拆点”，在构图过程中，匹配是双向的，即<u,v> 和<v,u>都算匹配，因此匹配数多了1倍，因此除以2得到原图的真正的匹配数。

最后剩下的问题就是求最大二分匹配数了，用匈牙利算法，这就不多说了，参考PKU3041的做法，基本一摸一样

从这道题得出了一个结论：

当二分图的两个顶点子集基数相等时，该二分图所有顶点的匹配数 等于 任意一个顶点子集匹配数的2倍 

#include<iostream>
#include<cstring>
#include<algorithm>
#define maxn 410
using namespace std;
bool vis[maxn];
char c[maxn][maxn];
int tx,ty,g[maxn][maxn];
int link[maxn],map[maxn][maxn];
int dir[][]={,,,-,-,,,};//上下左右
bool Find(int x){
       for(int i=;i<=ty;i++){//匹配右侧顶点集
           if(g[x][i]&&!vis[i]){
              vis[i]=true;
              if(!link[i]||Find(link[i])){
                 link[i]=x;
                 return true;
              }
           }
       }
   return false;
}
int maxMatch()
{
       int ans=;
       memset(link,,sizeof(link));
       for(int i=;i<=tx;i++){//枚举左侧顶点集
        memset(vis,false,sizeof(vis));
        if(Find(i))
            ans++;
       }
       return ans;
}
int main(){
    int T,m,n;
       cin>>T;
       while(T--){
           memset(g,,sizeof(g));
           memset(c,,sizeof(c));
           memset(map,,sizeof(map));
         cin>>m>>n;
          int cnt=;
          for(int i=;i<=m;i++){
            for(int j=;j<=n;j++){
                cin>>c[i][j];
                 if(c[i][j]=='*')
                    map[i][j]=++cnt;
            }
          }
          tx=cnt,ty=cnt;
         for(int i=;i<=m;i++){
            for(int j=;j<=n;j++){
                if(map[i][j]){
                    for(int k=;k<;k++){
                           int nx=i+dir[k][];
                        int ny=j+dir[k][];
                        if(nx<||nx>m||ny<||ny>n)
                            continue;
                        if(map[nx][ny])
                            g[map[i][j]][map[nx][ny]]=;
                    }
                }
            }
          }
          printf("%d\n",cnt-maxMatch()/);
       }
}

PS:之前一直想不通一点，为什么PKU3041可以直接用x,y坐标作边集。

PKU3041最后的图是对整行或者整列操作，拥有相同x坐标或y坐标的点看成了相同的，但这里是对单独的点操作，考虑它周围的点是否能连成边，再看能不能覆盖掉，这是不同的地方。