AtCoder ABC 130F Minimum Bounding Box

题目链接：https://atcoder.jp/contests/abc130/tasks/abc130_f

题目大意

　　给定地图上 N 个点的坐标和移动方向，它们会以每秒 1 个单位的速度移动，设 Ans(t) 为在 t 时刻，$(x_{max} - x_{min}) * (y_{max} - y_{min})$的值，求 Ans(t) 的最小值。(最小值可能不是一个整数)

分析

　　稍加思考可以发现，不是所有点的所有坐标都对答案有影响，很多点完全可以忽略不计，下面以 Y 坐标为例，讨论影响$(y_{max} - y_{min})$的值。

　　首先我们把 N 个点分为 3 类，向下移动的，向上移动的和水平方向移动的，具体如下图所示：

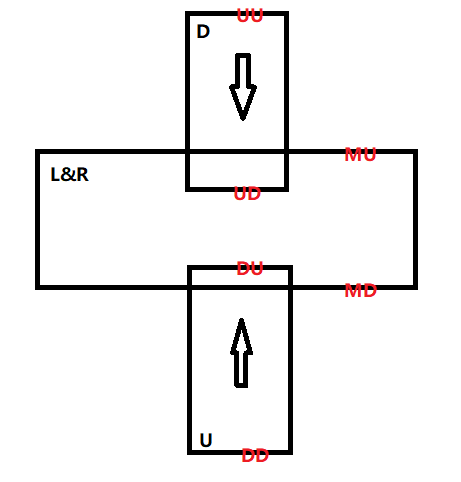
　　其中，UU 代表往下移动的点中 Y 坐标最大值，UD 代表往下移动的点中 Y 坐标最小值，其余同理。

　　我们发现，影响$(y_{max} - y_{min})$就是这 6 个值，当它们某两个值重合时就有可能改变答案。

　　X 坐标方向上也是同理，只要旋转一下即可。

　　当我们把 X 和 Y 坐标上对应的 6 个值都算出来的时候，把它们两两组合，暴力枚举所有可能时刻，就能求出最终答案。

代码如下

 #include <bits/stdc++.h>
 using namespace std;

 #define INIT() ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
 #define Rep(i,n) for (int i = 0; i < (n); ++i)
 #define For(i,s,t) for (int i = (s); i <= (t); ++i)
 #define rFor(i,t,s) for (int i = (t); i >= (s); --i)
 #define ForLL(i, s, t) for (LL i = LL(s); i <= LL(t); ++i)
 #define rForLL(i, t, s) for (LL i = LL(t); i >= LL(s); --i)
 #define foreach(i,c) for (__typeof(c.begin()) i = c.begin(); i != c.end(); ++i)
 #define rforeach(i,c) for (__typeof(c.rbegin()) i = c.rbegin(); i != c.rend(); ++i)

 #define pr(x) cout << #x << " = " << x << "  "
 #define prln(x) cout << #x << " = " << x << endl

 #define LOWBIT(x) ((x)&(-x))

 #define ALL(x) x.begin(),x.end()
 #define INS(x) inserter(x,x.begin())
 #define UNIQUE(x) x.erase(unique(x.begin(), x.end()), x.end())
 #define REMOVE(x, c) x.erase(remove(x.begin(), x.end(), c), x.end()); // 删去 x 中所有 c
 #define TOLOWER(x) transform(x.begin(), x.end(), x.begin(),::tolower);
 #define TOUPPER(x) transform(x.begin(), x.end(), x.begin(),::toupper);

 #define ms0(a) memset(a,0,sizeof(a))
 #define msI(a) memset(a,inf,sizeof(a))
 #define msM(a) memset(a,-1,sizeof(a))

 #define MP make_pair
 #define PB push_back
 #define ft first
 #define sd second

 template<typename T1, typename T2>
 istream &operator>>(istream &in, pair<T1, T2> &p) {
     in >> p.first >> p.second;
     return in;
 }

 template<typename T>
 istream &operator>>(istream &in, vector<T> &v) {
     for (auto &x: v)
         in >> x;
     return in;
 }

 template<typename T1, typename T2>
 ostream &operator<<(ostream &out, const std::pair<T1, T2> &p) {
     out << "[" << p.first << ", " << p.second << "]" << "\n";
     return out;
 }

 inline int gc(){
     static const int BUF = 1e7;
     static char buf[BUF], *bg = buf + BUF, *ed = bg;

     if(bg == ed) fread(bg = buf, , BUF, stdin);
     return *bg++;
 } 

 inline int ri(){
     int x = , f = , c = gc();
     for(; c<||c>; f = c=='-'?-:f, c=gc());
     for(; c>&&c<; x = x* + c - , c=gc());
     return x*f;
 }

 template<class T>
 inline string toString(T x) {
     ostringstream sout;
     sout << x;
     return sout.str();
 }

 inline int toInt(string s) {
     int v;
     istringstream sin(s);
     sin >> v;
     return v;
 }

 //min <= aim <= max
 template<typename T>
 inline bool BETWEEN(const T aim, const T min, const T max) {
     return min <= aim && aim <= max;
 }

 typedef long long LL;
 typedef unsigned long long uLL;
 typedef pair< double, double > PDD;
 typedef pair< int, int > PII;
 typedef pair< int, PII > PIPII;
 typedef pair< string, int > PSI;
 typedef pair< int, PSI > PIPSI;
 typedef set< int > SI;
 typedef set< PII > SPII;
 typedef vector< int > VI;
 typedef vector< double > VD;
 typedef vector< VI > VVI;
 typedef vector< SI > VSI;
 typedef vector< PII > VPII;
 typedef map< int, int > MII;
 typedef map< int, string > MIS;
 typedef map< int, PII > MIPII;
 typedef map< PII, int > MPIII;
 typedef map< string, int > MSI;
 typedef map< string, string > MSS;
 typedef map< PII, string > MPIIS;
 typedef map< PII, PII > MPIIPII;
 typedef multimap< int, int > MMII;
 typedef multimap< string, int > MMSI;
 //typedef unordered_map< int, int > uMII;
 typedef pair< LL, LL > PLL;
 typedef vector< LL > VL;
 typedef vector< VL > VVL;
 typedef priority_queue< int > PQIMax;
 typedef priority_queue< int, VI, greater< int > > PQIMin;
 const double EPS = 1e-;
 const LL inf = 0x7fffffff;
 const LL infLL = 0x7fffffffffffffffLL;
 const LL mod = 1e9 + ;
 const int maxN = 1e5 + ;
 const LL ONE = ;
 const LL evenBits = 0xaaaaaaaaaaaaaaaa;
 const LL oddBits = 0x5555555555555555;

 #define UU A[0]
 #define UD A[1]
 #define MU A[2]
 #define MD A[3]
 #define DU A[4]
 #define DD A[5]

 struct State{
     double A[] = {-inf, inf, -inf, inf, -inf, inf};
     double _max = -inf, _min = inf;

     State operator+ (const double &x) const {
         State ret = *this;
         if(fabs(ret.UU) < 1e9) ret.UU -= x;
         if(fabs(ret.UD) < 1e9) ret.UD -= x;
         if(fabs(ret.DU) < 1e9) ret.DU += x;
         if(fabs(ret.DD) < 1e9) ret.DD += x;

         Rep(i, ) {
             if(fabs(ret.A[i]) < 1e9) {
                 ret._max = max(ret._max, ret.A[i]);
                 ret._min = min(ret._min, ret.A[i]);
             }
         }
         return ret;
     }
 };

 int N;
 State X, Y;
 double ans = infLL;
 set< double > T; // 记录关键时间节点 

 int main(){
     //freopen("MyOutput.txt","w",stdout);
     //freopen("input.txt","r",stdin);
     //INIT();
     cin >> N;
     Rep(i, N) {
         double x, y;
         string d;
         cin >> x >> y >> d;

         if(d[] == 'U') {
             Y.DU = max(Y.DU, y);
             Y.DD = min(Y.DD, y);

             X.MU = max(X.MU, x);
             X.MD = min(X.MD, x);
         }
         if(d[] == 'D') {
             Y.UU = max(Y.UU, y);
             Y.UD = min(Y.UD, y);

             X.MU = max(X.MU, x);
             X.MD = min(X.MD, x);
         }
         if(d[] == 'R') {
             X.DU = max(X.DU, x);
             X.DD = min(X.DD, x);

             Y.MU = max(Y.MU, y);
             Y.MD = min(Y.MD, y);
         }
         if(d[] == 'L') {
             X.UU = max(X.UU, x);
             X.UD = min(X.UD, x);

             Y.MU = max(Y.MU, y);
             Y.MD = min(Y.MD, y);
         }
     }

     Rep(i, ) {
         Rep(j, ) {
             T.insert(fabs(X.A[i] - X.A[j]));
             T.insert(fabs(X.A[i] - X.A[j]) / );
             T.insert(fabs(Y.A[i] - Y.A[j]));
             T.insert(fabs(Y.A[i] - Y.A[j]) / );
             T.insert(fabs(X.A[i] - Y.A[j]));
             T.insert(fabs(X.A[i] - Y.A[j]) / );
         }
     }

     foreach(i, T) {
         if(*i > 1e9) break;
         State tmpX = X + *i;
         State tmpY = Y + *i; 

         ans = min(ans, (tmpX._max - tmpX._min) * (tmpY._max - tmpY._min));
     }

     printf("%.10f\n", ans);
     return ;
 }