[LOJ#3022][网络流]「CQOI2017」老 C 的方块

• 题目传送门

• 定义有特殊边相邻的格子颜色为黑，否则为白

• 可以看出，题目给出的限制条件的本质是如果两个小方块所在的格子 \(x\) 和 \(y\) 为两个相邻的黑格，那么 \(x\) 和 \(y\) 之间必然有一者满足其上下左右的所有白格内都没有小方块

• 即对于这样的 \(x\) 和 \(y\) ，需要以下三个条件至少满足一个：

• （1）用 \(\min(w_x,w_y)\) 的代价删除 \(x\) 和 \(y\) 上的其中一个小方块

• （2）把与 \(x\) 相邻的白格内的小方块全部删掉

• （3）把与 \(y\) 相邻的白格内的小方块全部删掉

• 故考虑对于所有的白格 \(i\) ，拆成两个点 \(i_0\) 和 \(i_1\) ，并连边 \(<i_0,i_1,w_i>\)

• 对于所有的黑格组（相邻且之间有特殊边的两个黑格）\((x,y)\) ，也建立两个点，第一个点向第二个点连容量为 \(\min(w_x,w_y)\) 的边

• 这时候我们就有一个比较明显的最小割模型了

• 即对于需要「至少满足一个」的条件集合进行串联，需要「全部满足」的条件集合进行并联

• 具体地，如下图：

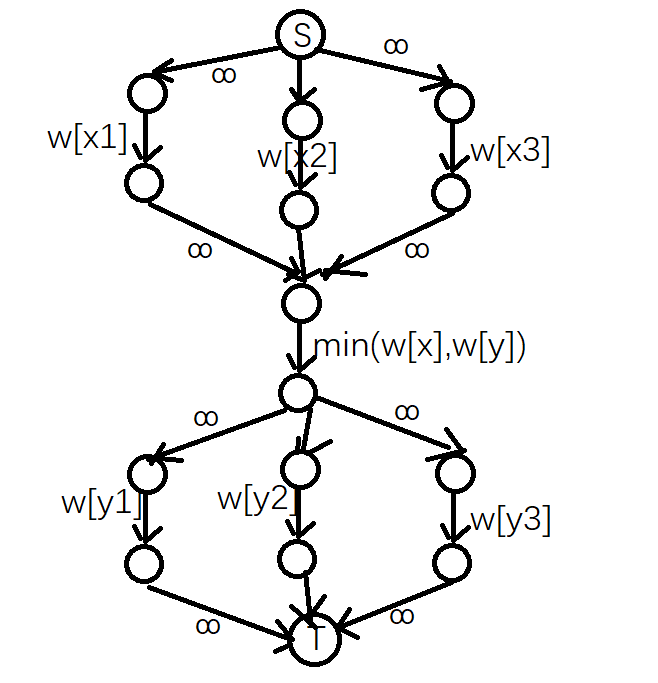
• 其中 \(x_1,x_2,x_3\) 表示与 \(x\) 相邻的白格， \(y_1,y_2,y_3\) 同理

• 以下设上图中 \(x_1,x_2,x_3\) 对应的三条边在第一层， \(\min(w_x,w_y)\) 对应的边在第二层， \(y_1,y_2,y_3\) 对应的三条边在第三层

• 至于 \(\min(w_x,w_y)\) 的边为什么一定要放在中间，后面会说

• 我们会发现一个问题：一个白格会属于 \(3\) 个黑格，直接建图会导致不同的黑格组之间互相影响

• 所以正确的建图方式是：设 \(x\) 在 \(y\) 左边，则要判断黑哥所在行号的奇偶性

• 若在奇行则 \(S\) 到 \(T\) 的路径上依次限制与 \(x\) 相邻的白格 \(\rightarrow\) 黑格组 \((x,y)\) 本身 \(\rightarrow\) 与 \(y\) 相邻的白格，否则反过来

• 考虑这样做的正确性：易得这么建图可以使得对于任意一个白格对应的限制边只在一层（第一层或第三层）中出现

• 如果一个白格 \(i\) 同时属于两个黑格组且位于第一层，且边 \(<i_0,i_1>\) 没有被割掉，那么显然这两个黑格组的第一层限制都必然不会被满足了，这时即使不同的黑格组之间互相影响也不会对最终的答案造成影响。第三层同理

• 而这时候如果 \(\min(w_x,w_y)\) 不在第二层而在第一层，那么假设这时候 \(i\) 位于第二层，有两个黑格组 \(X\) 和 \(Y\) ，\(X\) 只割掉了第三层，\(Y\) 只割掉了第一层，那么由于保留了边 \(<i_0,i_1>\) 之后 \(X\) 和 \(Y\) 的第二层能互通，故这时源点到汇点有一条 \(S\rightarrow X_1\rightarrow X_2\rightarrow Y_2\rightarrow Y_3\rightarrow T\) 的路径，这时就不合法了

Code

#include <bits/stdc++.h>

template <class T>
inline void read(T &res)
{
	res = 0; bool bo = 0; char c;
	while (((c = getchar()) < '0' || c > '9') && c != '-');
	if (c == '-') bo = 1; else res = c - 48;
	while ((c = getchar()) >= '0' && c <= '9')
		res = (res << 3) + (res << 1) + (c - 48);
	if (bo) res = ~res + 1;
}

template <class T>
inline T Min(const T &a, const T &b) {return a < b ? a : b;}

const int N = 1e5 + 10, M = 3e5 + 5, L = 4e6 + 5, INF = 0x3f3f3f3f;

int n, X[N], Y[N], w[N], ecnt = 1, nxt[L], adj[M], go[L], cap[L], len, que[M],
lev[M], cur[M], S, T, ans;
std::map<int, int> is[N];

int which(int x, int op) {return (x << 1) + op;}

void add_edge(int u, int v, int w)
{
	nxt[++ecnt] = adj[u]; adj[u] = ecnt; go[ecnt] = v; cap[ecnt] = w;
	nxt[++ecnt] = adj[v]; adj[v] = ecnt; go[ecnt] = u; cap[ecnt] = 0;
}

bool bfs()
{
	for (int i = S; i <= T; i++) lev[i] = -1, cur[i] = adj[i];
	lev[que[len = 1] = S] = 0;
	for (int i = 1; i <= len; i++)
	{
		int u = que[i];
		for (int e = adj[u], v = go[e]; e; e = nxt[e], v = go[e])
			if (cap[e] && lev[v] == -1)
			{
				lev[que[++len] = v] = lev[u] + 1;
				if (v == T) return 1;
			}
	}
	return 0;
}

int dinic(int u, int flow)
{
	if (u == T) return flow;
	int res = 0, delta;
	for (int &e = cur[u], v = go[e]; e; e = nxt[e], v = go[e])
		if (cap[e] && lev[u] < lev[v])
		{
			delta = dinic(v, Min(cap[e], flow - res));
			if (delta)
			{
				cap[e] -= delta; cap[e ^ 1] += delta;
				res += delta; if (res == flow) break;
			}
		}
	if (res < flow) lev[u] = -1;
	return res;
}

void add(int i, int j, int op)
{
	if (op) add_edge(S, which(j, 0), INF), add_edge(which(j, 1), which(i, 0), INF);
	else add_edge(which(i, 1), which(j, 0), INF), add_edge(which(j, 1), T, INF);
}

int main()
{
	read(n); read(n); read(n);
	for (int i = 1; i <= n; i++)
		read(X[i]), read(Y[i]), read(w[i]), is[X[i]][Y[i]] = i;
	S = 1; T = n + 1 << 1;
	for (int i = 1; i <= n; i++)
	{
		if (X[i] % 4 != (Y[i] + 1) % 2 * 2 + 1 && X[i] % 4 != Y[i] % 2 * 2)
			add_edge(which(i, 0), which(i, 1), w[i]);
		if (X[i] % 4 != (Y[i] + 1) % 2 * 2 + 1) continue;
		int x = X[i], y = Y[i], j;
		if (!(j = is[x + 1][y])) continue;
		add_edge(which(i, 0), which(i, 1), Min(w[i], w[j]));
		if (j = is[x - 1][y]) add(i, j, y & 1);
		if (j = is[x][y - 1]) add(i, j, y & 1);
		if (j = is[x][y + 1]) add(i, j, y & 1);
		if (j = is[x + 2][y]) add(i, j, !(y & 1));
		if (j = is[x + 1][y - 1]) add(i, j, !(y & 1));
		if (j = is[x + 1][y + 1]) add(i, j, !(y & 1));
	}
	while (bfs()) ans += dinic(S, INF);
	return std::cout << ans << std::endl, 0;
}