题解【loj537】「LibreOJ NOIP Round #1」DNA 序列

题目描述

\(NOIP\)复赛之前\(HSD\)桑进行了一项研究，发现人某条染色体上的一段\(DNA\)序列中连续的\(k\)个碱基组成的碱基序列与做题的 \(AC\) 率有关！于是他想研究一下这种关系。

现在给出一段 \(DNA\) 序列，请帮他求出这段 \(DNA\) 序列中所有连续\(k\)个碱基形成的碱基序列中，出现最多的一种的出现次数。

输入格式

两行，第一行为一段 \(DNA\) 序列，保证 \(DNA\) 序列合法，即只含有 \(A, G, C, T\) 四种碱基；

第二行为一个正整数\(k\)，意义与题目描述相同。

输出格式

一行，一个正整数，为题目描述中所求答案。

样例

样例输入 1

AAAAA
1

样例输出 1

5

样例解释 1

对于这段 \(DNA\) 序列，连续的\(1\)个碱基组成的碱基序列只有

A，共出现\(5\)次，所以答案为\(5\)。

样例输入 2

ACTCACTC
4

样例输出 2

2

样例解释 2

对于这段 \(DNA\) 序列，连续的\(4\)个碱基组成的碱基序列为：

\(ACTC, CTCA, TCAC\)与 \(CACT\)。其中 \(ACTC\)出现\(2\)次，其余均出现 \(1\) 次，所以出现最多的次数为\(2\)，即为答案。

数据范围与提示

记 \(DNA\) 序列长度为\(n\)。

本题共\(10\)组数据，只有输出与标准输出一致才可以获得该测试点的分数。

下面给出每组数据的范围和满足性质情况：

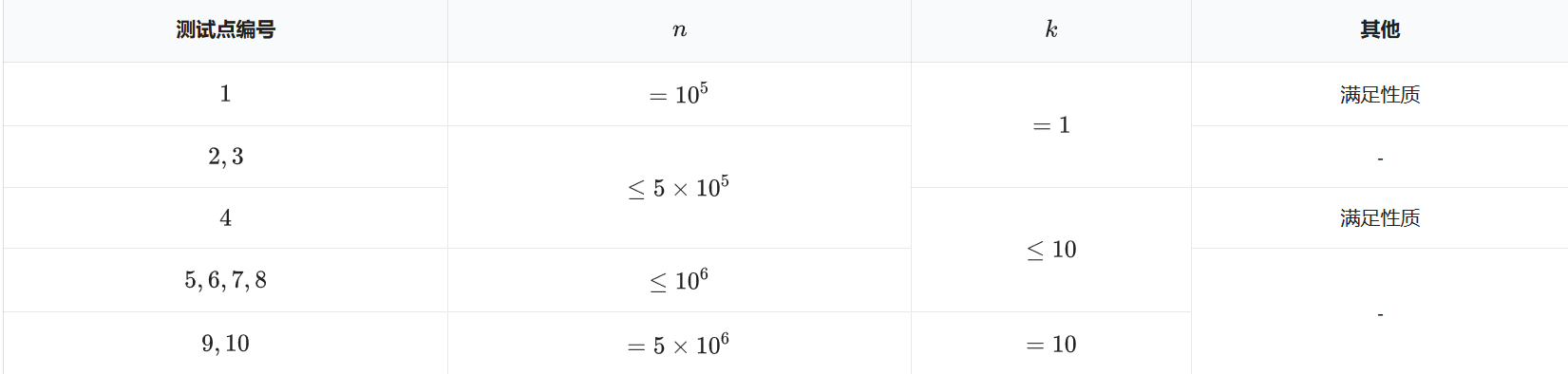
性质：给出的 \(DNA\) 碱基序列中每个碱基均相同。

对于所有数据均保证 \(k \leq n\)

题解

这题很容易想到用\(STL\)的\(map\)解决。

然而，经过本人的尝试，\(map\)在这题中只能得到\(80\)分的成绩，出题人会卡。

但是，\(unordered\)_\(map\)在此题中并不会被卡。

所以用\(unordered\)_\(map\)就可以啦\(QwQ\)。

（前提是评测开启\(C++11\)）

代码

#pragma GCC optimize(2)
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <cctype>
#include <string>
#include <unordered_map>

using namespace std;

inline int gi()
{
    int f = 1, x = 0; char c = getchar();
    while (c < '0' || c > '9') { if (c == '-') f = -1; c = getchar();}
    while (c >= '0' && c <= '9') { x = x * 10 + c - '0'; c = getchar();}
    return f * x;
}

string s;
int len, k, n, m, ans, js, p[9];
unordered_map <string, int> ap;

int main()
{
	cin >> s;
	k = gi();
	len = s.size();
	bool fl = true;
	for (int i = 1; i < len; i++)
	{
		if (s[i] != s[i - 1]) fl = false;
	}
	if (fl)
	{
		if (k == 1)
		{
			printf("%d\n", len);
			return 0;
		}
		else
		{
			printf("%d\n", len - k + 1);
			return 0;
		}
	}
	else if (k == 1)
	{
		for (int i = 0; i < len; i++)
		{
			if (s[i] == 'A') ++p[1];
			else if (s[i] == 'G') ++p[2];
			else if (s[i] == 'C') ++p[3];
			else ++p[4];
		}
		printf("%d\n", max(p[1], max(p[2], max(p[3], p[4]))));
		return 0;
	}
	else
	{
		for (int i = 0; i < s.size() - k + 1; i++) ++ap[s.substr(i, k)];
		for (auto it : ap) ans = max(ans, it.second);
		printf("%d\n", ans);
	}
	return 0;
}