CF981H K Paths

CF981H K Paths

题解

一道不错的分治ntt题目

题目稍微转化一下，就是所有k条链的存在交，并且交的部分都被覆盖k次

所以一定是两个点，之间路径选择k次，然后端点两开花

f[x]表示x子树内往下延伸k条链（可以停在x）的方案数（有标号）

每个子树选择一个或者不选择，最多一共选择k个，dp是O(n^2)的，

考虑生成函数，其实就是：

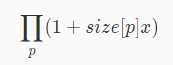
而

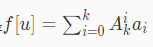
统计答案？

直接两两点对f相乘肯定不行，因为f仅仅是子树

考虑枚举x作为lca统计

如果是拐弯的链，树形DP即可。

而如果是直上直下的链，

对于不同子树，x的选择是扣去这个子树，还可以往上选择

分治NTT的经典问题

const int N=1e5+;
int n,k;
int jie[N],inv[N];
int A(int n,int m){
    if(n<||m<||n<m) return ;
    return mul(jie[n],inv[n-m]);
}
int val[N],si[N];
void divi(int l,int r,Poly &f,Poly &g){
    // cout<<" divi "<<l<<" "<<r<<endl;
    if(l==r){
        g.resize();g[]=val[l];
        f.resize();f[]=;f[]=si[l];
        return;
    }
    Poly lf,lg,rf,rg;
    int mid=(l+r)>>;
    divi(l,mid,lf,lg);
    divi(mid+,r,rf,rg);
    f=lf*rf;
    g=(lf*rg)+(lg*rf);
}
int f[N],sum[N],son[N];
int ans,sz[N];
struct node{
    int nxt,to;
}e[*N];
int hd[N],cnt;
void add(int x,int y){
    e[++cnt].nxt=hd[x];
    e[cnt].to=y;
    hd[x]=cnt;
}
void dfs(int x,int fa){
    // cout<<" xx "<<x<<" fa "<<fa<<endl;
    sz[x]=;
    int pre=;
    for(reg i=hd[x];i;i=e[i].nxt){
        int y=e[i].to;
        if(y==fa) continue;
        ++son[x];
        dfs(y,x);
        sz[x]+=sz[y];
        sum[x]=ad(sum[x],sum[y]);
        ans=ad(ans,mul(pre,sum[y]));
        pre=ad(pre,sum[y]);
    }
    if(son[x]){
        Poly F,G;
        int ct=;
        for(reg i=hd[x];i;i=e[i].nxt){
            int y=e[i].to;
            if(y==fa) continue;
            val[++ct]=sum[y];
            si[ct]=sz[y];
        }
        divi(,ct,F,G);
        Poly T;
        T.resize();
        T[]=;T[]=n-sz[x];
        G=G*T;
        for(reg i=;i<=min(k,son[x]);++i){
            // cout<<"F["<<i<<"] "<<F[i]<<" G["<<i<<"] "<<G[i]<<endl;
            ans=ad(ans,mul(A(k,i),G[i]));
            f[x]=ad(f[x],mul(A(k,i),F[i]));
        }
        sum[x]=ad(sum[x],f[x]);
    }else{
        f[x]=;sum[x]=;
    }
    // cout<<" return "<<x<<" f "<<f[x]<<endl;
}
int main(){
    rd(n);rd(k);
    if(k==){
        ans=(ll)n*(n-)/%mod;
        ot(ans);return ;
    }
    jie[]=;
    for(reg i=;i<=k;++i) jie[i]=mul(jie[i-],i);
    inv[k]=qm(jie[k],mod-);
    for(reg i=k-;i>=;--i) inv[i]=mul(inv[i+],i+);

    int x,y;
    for(reg i=;i<n;++i){
        rd(x);rd(y);add(x,y);add(y,x);
    }
    dfs(,);
    ot(ans);
    return ;
}

}
signed main(){
    Miracle::main();
    return ;
}

/*
   Author: *Miracle*
   Date: 2019/4/8 18:57:00
*/