用于扩展目标跟踪的笛卡尔B-Spline车辆模型

(哥廷根大学)

摘要

文章提出了一种表示空间扩展物体轮廓的新方法，该方法适用于采用激光雷达跟踪未知尺寸和方向的车辆。我们在笛卡尔坐标系中使用二次均匀周期的B-Splines直接表示目标的星 - 凸形状近似。与之前在极坐标下工作的方法相比，我们引入了一个新的步行参数来模拟物体的轮廓功能，使得形状参数很好地被定义，并且与测量值位于同一空间内。该方法的主要优点是可以通过缩放样条的基点来独立地执行长度和宽度的缩放。

一、引言

　　对于汽车领域，特别是高级驾驶辅助系统（ADAS）功能，扩展目标跟踪（EOT）的方向最近引起了很多关注。在该领域中，跟踪其他交通参与者是在自动驾驶车辆竞赛中需要解决的重要挑战。对于这一挑战，部署具有极高空间分辨率的传感器，用于车辆环境和其他交通参与者的感知。这种传感器的一个例子是汽车激光雷达，它提供了一系列来自环境的点测量。这项工作涉及EOT领域，与经典对象相比，可以同时从同一目标观察到多个测量。从而提供有关目标范围（extent）的信息。EOT的目的是估计目标的运动参数及其随时间变化的形状或边界参数 。EOT领域概述详见参考文献一。

　　 对于其他交通参与者的感知而产生的重要问题是用于表示道路上的其他车辆的模型，这个模型必须具有灵活性，但要针对特定​​应用进行动态定制。为了表示扩展对象，已经开发了不同的目标模型。在参考文献2中，提出了EOT的随机超曲面模型，并利用傅立叶系数在参考文献三中实现了星 - 凸约束的应用。用于单传感器系统(参考文献7)以及多传感器系统（参考文献8）的单目标跟踪器（参考文献4~6）以及的多目标滤波器，已经以高斯过程模型的形式开发了更多的星 - 凸方法。 用于模拟目标范围的矩形多边形的专用模型，已被用于跟踪车辆（参考文献9）。通过水平集在（参考文献10）中提出了一般多边形跟踪器的基础。对于目标的长度和宽度感兴趣的应用，椭圆模型适合于基于目标体积的测量源来描述扩展目标（参考文献11~13）。自动驾驶中使用的另一种传感器是radar，与激光雷达相比，radar测量可提供目标的多普勒速度-测量结果可来自目标体积。为了结合这些信息，在（参考文献14 15）中开发了不同的扩展目标模型。在这项工作中，我们建议使用笛卡尔定义的均匀B样条来对LIDAR数据建立目标轮廓。通常这种方法允许在笛卡尔坐标中用参数来模拟几乎任意的连续表面。因此，不需要改变表面参数和测量之间的坐标系。存在利用样条线的EOT的进一步相关工作。我们发现在（参考文献16）中，星 - 凸轮廓的径向函数用均匀的B样条表示，同时还有解耦形状和运动参数。另外，一批跨多个时间的测量值用于更新形状参数。（参考文献17）利用样条线跟踪细长的扩展物体，其中物体形状通过沿样条线对齐的一组箱子建模，该样条线解释了例如街道汽车的伸长率和曲率。在第二节中，将提供对一般笛卡尔对象边界的定义。将使用第II-A节中的二次均匀周期B样条来描述连续笛卡尔模型的实现。
在第III节中，这个模型将会被用于跟踪车辆的估计，并且与使用高斯过程评估模型进行比较。

二、扩展目标跟踪问题

　　与经典目标跟踪相比，扩展目标产生0≤mk≤nk的测量值，在典型的EOT场景中，在每个时间步k接收的一组nk噪声损坏的点测量值{yk，l} nk l = 1。对于给定测量模式的解释数据显著增加。这可能通过这些模式携带的附加信息得到一定程度的补救，这可以估计目标的运动状态x_kin以及它们的范围状态x_shape。因此，典型的EOT状态由x = [m，ψ，x_kin，x_shape]给出，分别具有位置m和方向ψ。为了模拟可能的测量源，(参考文献2)指定轮廓函数C（α，xshape）∈R2，其中α是表面函数的简单参数化。根据场景和传感器类型，测量值zl可以源自目标表面或体积。对于以下讨论，相对目标中心写入表面轮廓函数是方便的，即C（α，x）= m +Rψ·C（α，x_shape）.旋转矩阵Rψ由方向ψ定义。在以下部分中，我们将C（α，x_shape）称为C（α），省略形状参数xshape以获得更好的可读性。对于不同类型的形状参数来对对象轮廓进行建模对应着不同的方法，其中最突出的是径向函数的应用，即轮廓分解为φ方向的单位向量uφ和标量函数Crad（φ，x_shape）∈R，它描述了从中心到边界的距离,即C(α = φ, xshape) = uφ · Crad(φ, xshape)，根据定义，这种形状是星凸形状的。最近使用径向函数描述扩展目标的例子在（参考文献4）中给出，在那里，作者通过有限数量的测试输入及其相应的函数值，通过高斯过程定义径向函数。高斯过程的使用允许作者递归地估计任意形状，甚至应用对称约束来解释先验知识。从定义可以看出，这种设置对于类似于圆形的形状非常有效。但是强烈的各向同性形状，例如非常细长的矩形，或者在小的角度变化上具有大​​的半径变化的形状难以描述。在高斯过程的情况下，需要将定制的测试输入分布与依赖于方向的相关核组合，而模型通过傅里叶变换需要任意量的傅立叶系数来模拟依赖于方向的边界。造成这些困难的根本原因在于，并非所有形状，甚至仅限于星形的形状，同样在极坐标中得到很好的描述。这个问题是我们方法的主要动机，目标是根据可在随机超曲面模型中使用的任意形状目标的可微函数来提供直观描述。我们特别感兴趣的是，难以建立的在径向函数方面的描述，和反过来提供例如高斯过程或傅里叶系数等值线的补充方法。

A.　　B-Splines Countour Function

为了模拟边界C（α），我们应用周期均匀二次B样条并引入抽象步行参数τ，其将用作干扰参数，使得α：=τ。样条是一个分段定义的连续多项式函数（参考文献18 19）。通常，B样条B（τ）是Nb基函数Bn（τ）的加权和，n∈{0，...，Nb  -  1}

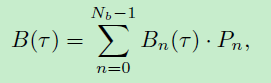
具有权重Pn和步行参数τ∈T：= [0，Nb]。该和可以表示为矩阵乘法 B（τ）=（P0，...，PNb-1）·Bs，Bτ=（B0（τ），...，BNb-1（τ））T。这里每个基函数都有一个通过 knots {k0，...，kNb}定义的有限支持，其中kj∈T，∀j。

在下文中，我们将列出与本文背景相关的一系列属性。详细参考可以在（参考文献18）中找到：

• 如果所有节点在区间[0，Nb]上等间隔，则B样条被称为均匀。
• 如果基函数，权重和相应的节点是周期性定义的，则B样条被称为周期性的。为了跨越转变点，这需要额外的d-1个结，即总共Nb + d-1，其中d是由Bn（τ）表示的多项式的次数。然而，对于所有i∈N，BN b + i（τ）= Bi（τ）= PN b + i = Pi，改变的结数N b = Nb + d  -  1。注意，在周期函数的上下文中，为简单起见，我们将N b称为Nb
• 样条具有d-1个连续导数。在二次B样条的情况下，我们强制执行1个连续导数。
• 通过为两个连续的基函数分配相同的权重，样条允许降低两个段之间连接的程度和连续性使得相同的结被定义两次。因此，多边形轮廓模型是二次样条模型的特殊情况，其中每个权重被定义两次，从而产生线段。

在下图中可以找到具有12个控制点和具有双重定义结的相应形状的示例十字形状，其中控制点位于十字的角上。

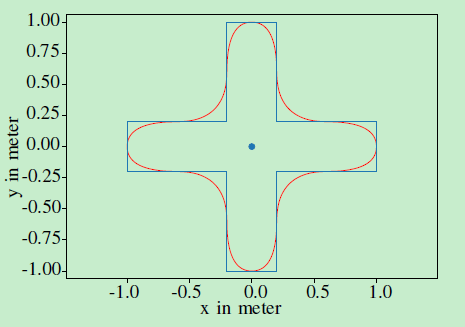
周期均匀二次基函数（参考文献18）的简单定义由下式给出：

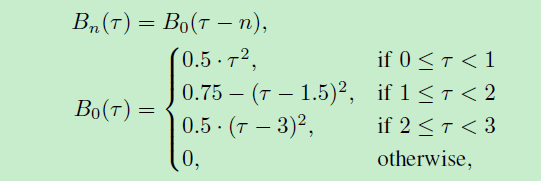
Nb knots是定义在整数{0,1，...，Nb}中。对于基函数B0（τ），定义的结是[0,1,2,3]，而每个其他基函数的定义结移动了它们各自的索引。注意，对于任何给定的τ，恰好有三个基函数是有效的。通过上述定义，我们能够通过周期均匀二次B样条建模笛卡尔轮廓函数C（τ）。反过来，局部坐标中的表面由以下公式定义：

其中P包含样条曲线在x和y维度上的有序权重，并完全定义轮廓的形状。在下文中，我们将P作为基点。
　　请注意，如果测量值来自目标边界，则基于样条曲线的轮廓的上述定义通常可以处理非星形凸形状，但必须以与多边形跟踪方法类似的方式用来自物体体积的测量值方式修改（参考文献17）。另一方面，如果施加的是星凸形状，则自动驾驶中的典型目标（如汽车、行人）不会受到影响。然而，这种限制允许对表面关联技术进行简单且有效的测量，并且具有允许在径向函数形状和样条形状之间进行直接比较的额外益处。反过来，我们将局限于本文其余部分的star-convex模型。

B.   Surface Point Association

　　已知的扩展目标跟踪的挑战是目标表面上的测量值和测量源之间的关系是未知的。这意味着所接收的观测结果不包含负责观察测量（参考文献1）的干扰参数τ。然而，以一个或一组测量源假设的形式用于与表面的某种关联是需要的。对于这项工作，我们定义一个假设τi和对象轮廓h（τi，x）上的相应位置，它提供了最佳估计：用给定的得分函数f（τ| y）。

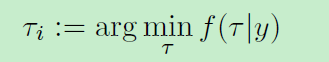
在不同的径向定义轮廓模型（参考文献2和4）中使用的有效关联模型是通过从形状中心到测量的相对于状态方向的相对角度的关联。该关联使用径向距离的得分并且提供具有零得分的唯一全局最小值。更一般的关联方案例如是测量与目标表面上具有与测量的最小距离的点的关联，因为它可以用在一些多边形跟踪器中（参考文献10 14）。为了简单起见，为了更好地与现有技术的径向定义轮廓模型进行比较，在我们对车辆进行星凸形状模拟的条件下，我们将在这项工作中使用径向关联。应该注意，可以另外使用定义到物体表面的距离的分数函数。在二次B样条线段上测量的最近点可以导出为三次多项式的一个唯一根，或者使用凸包，并且省略了星 - 凸边界的必要性。由于这个原因，我们可以说明允许找到测量yi的相应τi的不同条件，并且用它来表示轮廓上的相关点zi = h（τi，x），其中i表示测量指数。此外，我们将在形状局部坐标系中计算τi。此过程需要测量y和目标/局部坐标zi中的测量源，可以计算为

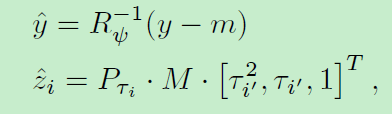
τi=τi-k（τi）和R-1ψ=RTψ，其中Pτ是三个有效基点。可以相对于每个结的表面点的角度来评估有效基点。从中心到测量的线的角度之间的相邻节点角限定了有效基函数（在星 - 凸物体的情况下）。用k（τi）∈{k0 ,.。。，kNb}是定义τi和three的三个有效基点的结

乘法的矩阵表示如式（6）中隐含的那样。为简单起见，我们将公式11中的扰乱参数独立部分说明为

由于τi的定义，我们可以将边界和测量的关系表示为

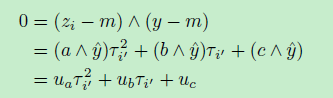
我们定义uq =q∧y，其中∧作为叉积。对于预期测量点的唯一性，我们还需要定义（z  -  m）·（y  -  m）≥0的约束。

　　可以很容易地获得这种程度的两个多项式的解，而我们仅使用关于我们约束的负根。因此，我们可以用τi=τi+ k（τi）来表示

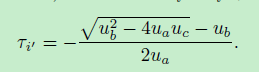
如果有效贝塞尔曲线段是线段，我们得到ua = 0，这将导致零分割。在这个特殊情况下，τi评估为

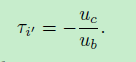
C. Spline Model:Jacobian

为了使用B-Spline模型跟踪扩展对象，需要实现贝叶斯过滤器。由于样条配方的非线性，可以应用Unscented卡尔曼滤波器（UKF）或扩展卡尔曼滤波器（EKF）。为此，我们将实施EKF(参考文献20)。具有时间索引k的EKF的标准方程是：

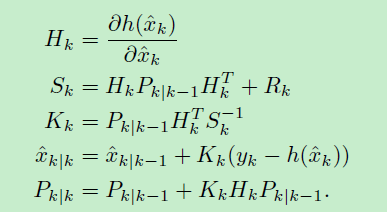
EKF需要计算在前一节中定义的预测测量值h（xk）和模型雅可比矩阵Hk。将描述雅可比行列式的计算，为此目的，我们要强调τi相对于状态参数的导数等于τi的导数。为了同时积分在时间k接收的测量值{yk，l} nk l = 1和每个yk的相应的相关扰乱参数τi，我们可以说明堆积量

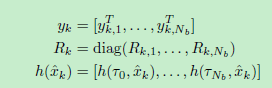
在这项工作中，我们将把这个模型应用于恒定但可扩展的星形 - 凸形车辆形状，其侧面为线段，角点为二次线段。我们通过将基点放置为矩形框来强制执行星 - 凸形状。如前所述，跟踪车辆不需要完全自由的形状参数。相反，如在盒子跟踪器的情况下，应该提供给定轮廓的非均匀可缩放版本，使得可以对卡车和小型汽车进行相似的建模。由于笛卡尔坐标中的定义，很容易引入非均匀缩放因子

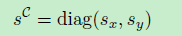
使用sx，sy是x和y维度中的缩放参数，这样

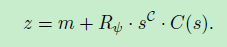
通过样条模型的定义，缩放简单地转换为给定但是恒定集合P的基础点PC的缩放比例并且扩展它，使得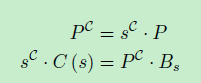

该定义允许减少参数

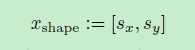
在下面的雅可比行列式推导中，我们将使用sc = diag（sy，sx）。这样缩放因子被应用于测量。因此，利用用于测量yi的相应的烦扰参数τi，雅可比矩阵求值为

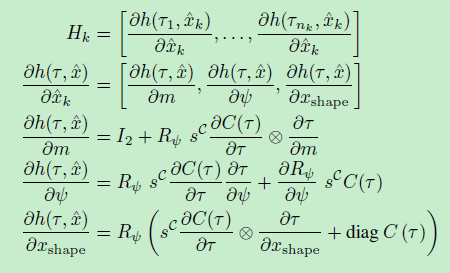
随着轮廓的导数

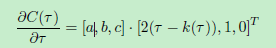
利用s的导数对其中一个状态参数进行评估

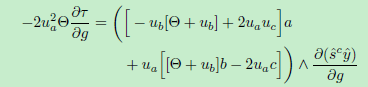
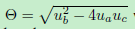在线段的情况下减少到：

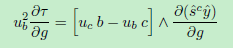在这里，我们在右侧使用带有矩阵的交叉积。我们将其定义为类似于点积的列式交叉产品，即

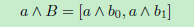
列向量a，b0，b1∈Rn和

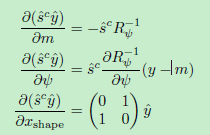
得到的关联和示例性EKF更新如图3所示。

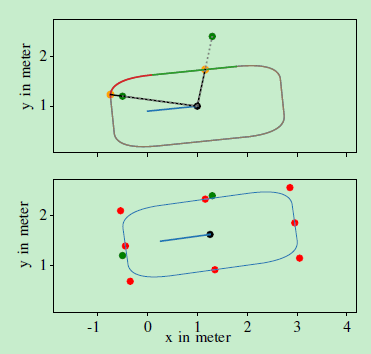
图3：两次测量的EKF更新示例为绿点。上图显示了虚线形式的径向源关联，相应的黄色表面点与表面上相应的贝塞尔曲线段分别以红色和绿色显示。下图显示了EKF更新后的形状。我们还提供了八个基点作为红点。

三、建模

　　对形状轮廓建模需要对所有形状参数进行微调，在高斯过程或另一个径向定义的轮廓的情况下，这意味着调整基角以及它们对应于表面的相应距离函数和相应的核函数。尝试使用相同的角度和内核值来模拟调整良好的对象的细长版本可能会产生强烈的副作用，例如边界函数的振荡。与径向函数相比，笛卡尔定义的模型只需要调整它控制点以解释边界的类似变化。为了延长给定对象，控制点在一个方向上缩放。所描述的对两种功能的影响显示在图4的左侧部分中。这里高斯过程需要至少20个微调基角来模拟形状和形状的长直段足以抑制功能振荡。样条曲线模型使用笛卡尔坐标中的八个点，因此，16个参数用于描述形状，而没有利用对称性，并且给出了信息无损扩展性。对于以下部分，先前的模型将是右图部分中提供的微调轮廓的均匀缩放版本。

1）形状缩放

使用样条曲线在笛卡尔坐标系中建模车辆形状的一个优点是对基点的解释。它允许通过缩放基点本身来直接非均匀缩放任何星 - 凸物体的形状，而缩放径向函数的形状参数仅允许均匀缩放。非均匀缩放的实现将需要从径向参数到笛卡尔的映射以及在每次计算中缩放的形状与非缩放角度的角度，这是因为状态参数在两个不同的空间中定义，再次使形状模型更加不直观，难以处理。Spline模型中非均匀缩放的优点如图5所示在简单的10个步骤之后产生的形状提供了均匀可缩放高斯过程的边界多边形以及非均匀可缩放样条模型的相同结果。

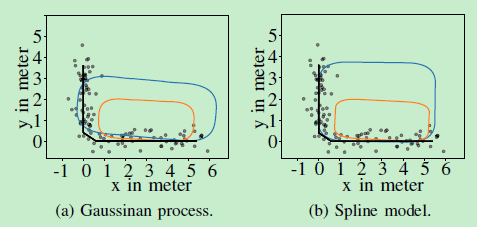
图5：高斯过程与样条模型的缩放更新，橙色的先前目标估计，蓝色的10次EKF迭代后的目标估计，灰度​​点的测量的比较。

这些测量值在x和y维度上以0.12米的方差生成，并且每个时间步长提供20个测量值。两种型号的测量都非常适合它们的局限性。样条曲线模型调整其长度和高度以表示对象，而高斯过程仅能够表示形状的均匀缩放版本，因此，它不能表示形状以及样条曲线模型。

2）运动模型：

　　 我们将假设我们的目标根据协调的转弯运动模型（参考文献21）移动并使用EKF来预测目标。使用的运动学参数是：

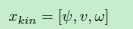
将航向ψ作为状态参数的一部分，作为ψ的导数的偏航角ω和作为m的导数的速度v被建模为状态参数。ω和v的导数被建模为假设为具有相应协方差Σω和Σa的正态分布随机变量。该假设是在车辆跟踪的背景下进行的。

3）对象跟踪：

　　为了评估样条曲线形状模型的跟踪性能，将与高斯过程进行比较。为了能够比较两种方法的跟踪性能，我们将采用恒定的形状，因为不同的缩放方法使得比较非常困难.测试数据是汽车LIDAR扫描仪提供的单个对象的点云。在这种情况下，测量协方差设置为R = diag（0.02,0.02）。具有恒定比例参数的状态表示为xstate =（m，ψ，v，ω），其中m为米，转角为ψ，v为每秒米，ω为辐射/秒，噪声项为各个单位。协调转弯运动模型的过程噪声协方差设置为Σa= 2.2和Σw= 1.5。直线轨迹上的两种跟踪算法的结果可以在下图中找到。

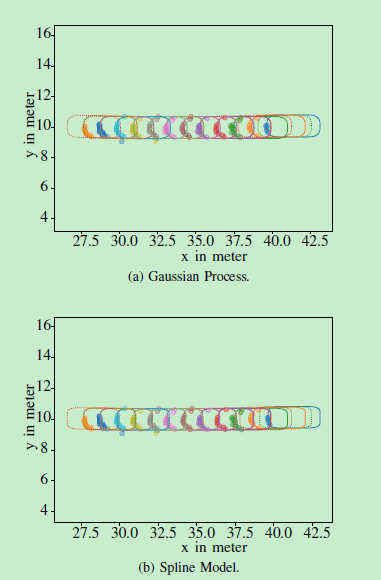
图6：在包含预测估计（虚线形状），校正估计（全形状）和每个时间步长的相应测量（点）的直线轨迹上的样条模型和高斯过程的每第4个步骤的图表相同的颜色。

而在弯曲轨道上的结果可以在图7中找到：

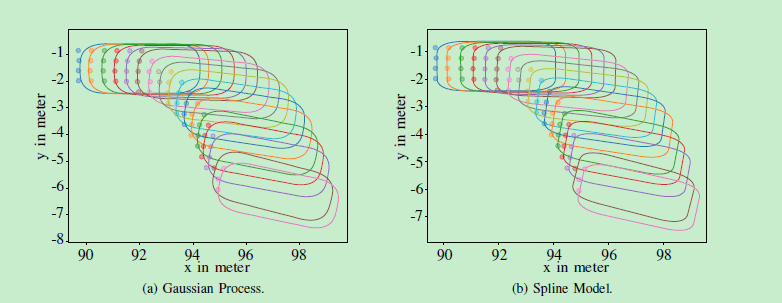
图7：在曲线轨迹上的样条模型和高斯过程的每第4个步骤的曲线图，校正的估计（完整形状）和相同颜色的每个时间步长的相应测量（点）。

状态先验在直线轨迹中设定为m0 =（41,10，π，0,0）并且在弯曲状态中设定为m0 =（92.0，-1.5,0.0,0）。两种情况下的先验协方差矩阵设置为P0 = diag（10,10,0.01,5,5）。除了随时间变化的跟踪形状之外，两种算法的状态参数以及测量到其源的创新和关联对数可能性在图8中提供，用于具有相应差异的弯曲轨迹。

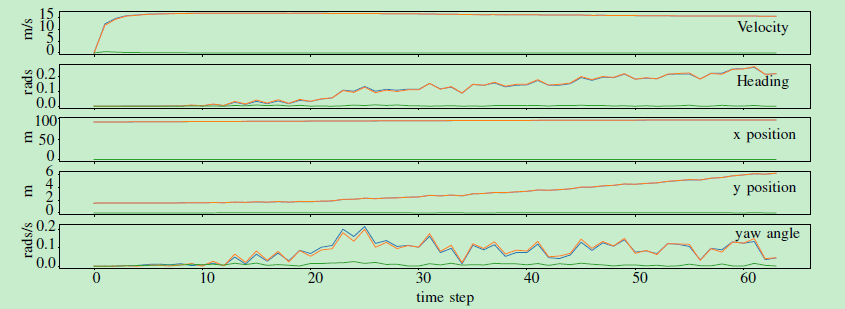
（a）状态参数及其差异。Spline模型的状态参数为蓝色，高斯过程的状态参数为橙色，它们之间的差异为绿色。

图8：橙色高斯过程的测量关联和创新可能性以及蓝色随时间变化的样条模型的可能性。左图显示关联日志可能性，右图显示创新日志可能性以及它们在绿色方面的差异。

所有因素都显示出彼此显着的相似性，这支持了两种方法在给定形状的性能中的等效性。请注意，由于形状不相同，我们不期望两种模型具有完全相同的行为。尽管如此，状态参数在所有时间步长上彼此接近，但偏航角除外，平均角度在模型之间相差0.0086，最大值为0.025。两种可能性都遵循相同的趋势。关联对数可能性在10-4的范围内不同，而创新对数可能性在更显着的程度上变化，平均偏差为0.23。似然的相似性很重要，它允许为当前实现高斯过程的每个多目标跟踪器使用提供的样条模型作为用于跟踪车辆的扩展对象模型[7]。

 四、结论和未来的工作

　　在这项工作中，已经提出了用于跟踪扩展物体（特别是车辆）的笛卡尔均匀B样条模型。已经表明，汽车LIDAR数据的跟踪性能与实际数据上的现有技术跟踪算法相当。该新模型的主要优点是可以对物体轴进行独立的二维缩放，并且可以对边界相关的状态参数进行直观的描述。将来，车辆型号可以扩展到其他传感器，如汽车雷达。可以研究对潜在凹形的应用，尤其是关于水平集多边形跟踪方法[10]。还应该注意的是，Splines通常被很好地探索，以便存在不同的变体和实现，其包含可以被EOT利用的进一步的约束和特征。Spline模型关联的另一种选择是使用基于EM方法的跟踪器，如[22]中所讨论的，它不需要单个源假设。作为本文所述的EKF的替代方案，可以部署UKF来解决非线性估计问题。