支持向量机-SVM 学习
一 、支持向量机(SVM)
1.1 符号定义
标签 y 不再取 0 或 1,而是: y∈{-1, 1}
定义函数:
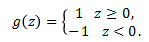
向量,没有第 0 个维度,b 为截距,预测函数定义为:

1.2 函数间隔与几何间隔
1.2.1 函数间隔
样本个体:

全体:

1.2.2 几何间隔
样本个体:

全体:
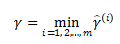
1.2.3 关系
函数间隔与几何间隔都是对预测置信度的度量,这个间隔越大,说明预测样本离着分界线越远,我们预测的结果也就更加可靠。

1.3 优化目标
假设样本是线性可分的,优化目标为
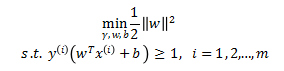
1.4 广义拉格朗日乘数法
带约束的优化为:
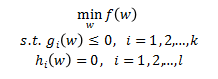
转化为:
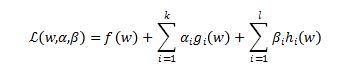
【原始问题】:
记量 为:
为: 
原始问题为:
【对偶问题】:
记量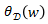 为:
为: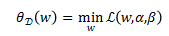
对偶问题为: 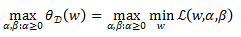
对于原始问题和对偶问题,以下关系恒成立:
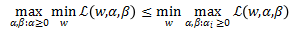
KKT条件:

当KKT条件满足时,对偶问题和原始问题有着相同的解。
1.5 最优间隔分类器
SVM的拉格朗日乘数法:
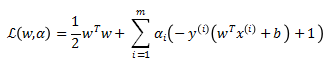
原始问题:
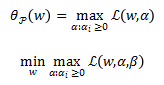
对偶问题:

根据KKT条件:
对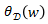 关于
关于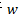 求梯度,令之为0,可得:
求梯度,令之为0,可得:
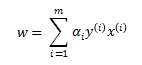
对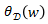 关于 b 求导,令之为0,可得:
关于 b 求导,令之为0,可得:
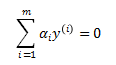
带回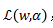 ,得:
,得:

因此SVM的对偶问题为:

将对偶解 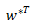 带入原始问题,对所有的
带入原始问题,对所有的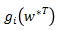 不等于 0 对应的系数
不等于 0 对应的系数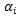 求导,令其等于0,得:
求导,令其等于0,得:

因为 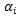 不为的项
不为的项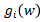 为0,即该点为支持向量。理想情况分割线两侧各有一个最近的点,且我们也仅在两侧各取一个点。因此,对于
为0,即该点为支持向量。理想情况分割线两侧各有一个最近的点,且我们也仅在两侧各取一个点。因此,对于 的,两侧同时乘 -1,累加两个式子得:
的,两侧同时乘 -1,累加两个式子得:
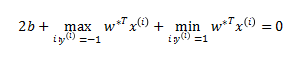
即:

上述算法称为最优间隔分类器。
1.6 SVM核
将 中的内积
中的内积 替换为
替换为 ,称
,称 为核。核 K 的合法取法有很多,如:
为核。核 K 的合法取法有很多,如:
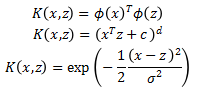
不同的核将 x 和 z 映射到了不同的空间之中,一组低维的向量投射至高维通常更容易划分。
1.7  正则化与软间隔
正则化与软间隔
对于一些线性不可分的情况,或者为了抵制噪音的影响,使用 软边距进行处理。为每组数据加入一个允许误差
软边距进行处理。为每组数据加入一个允许误差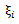 ,同时在优化目标中加入惩罚项
,同时在优化目标中加入惩罚项 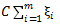 。SVM的原始优化问题变为:
。SVM的原始优化问题变为:
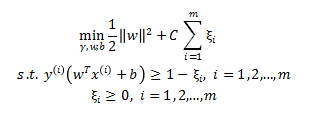
拉格朗日乘数法写作:
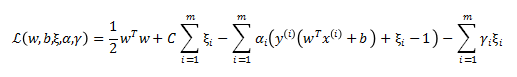
根据KKT条件,
令 ,得:
,得: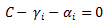
令 ,得:
,得:
令 ,得:
,得:
同样求对偶问题得到:

根据KKT条件,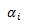 取值的关系如下:
取值的关系如下:
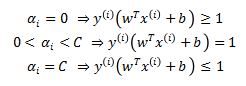
注意,b 不再是原始SVM的取值。
【Reference】
1. 支持向量机通俗导论(理解SVM的三层境界) 【这篇写的非常好】
支持向量机-SVM 学习的更多相关文章
- OpenCV 学习笔记 07 支持向量机SVM(flag)
1 SVM 基本概念 本章节主要从文字层面来概括性理解 SVM. 支持向量机(support vector machine,简SVM)是二类分类模型. 在机器学习中,它在分类与回归分析中分析数据的监督 ...
- 支持向量机通俗导论(SVM学习)
1.了解SVM 支持向量机,因其英文名为support vector machine,故一般简称SVM,通俗来讲,它是一种二类分类模型,其基本模型定义为特征空间上的间隔最大的线性分类器,其学习策略便是 ...
- 转:SVM与SVR支持向量机原理学习与思考(一)
SVM与SVR支持向量机原理学习与思考(一) 转:http://tonysh-thu.blogspot.com/2009/07/svmsvr.html 弱弱的看了看老掉牙的支持向量机(Support ...
- coursera机器学习-支持向量机SVM
#对coursera上Andrew Ng老师开的机器学习课程的笔记和心得: #注:此笔记是我自己认为本节课里比较重要.难理解或容易忘记的内容并做了些补充,并非是课堂详细笔记和要点: #标记为<补 ...
- Stanford机器学习---第八讲. 支持向量机SVM
原文: http://blog.csdn.net/abcjennifer/article/details/7849812 本栏目(Machine learning)包括单参数的线性回归.多参数的线性回 ...
- SVM学习笔记
一.SVM概述 支持向量机(support vector machine)是一系列的监督学习算法,能用于分类.回归分析.原本的SVM是个二分类算法,通过引入“OVO”或者“OVR”可以扩展到多分类问题 ...
- 【IUML】支持向量机SVM
从1995年Vapnik等人提出一种机器学习的新方法支持向量机(SVM)之后,支持向量机成为继人工神经网络之后又一研究热点,国内外研究都很多.支持向量机方法是建立在统计学习理论的VC维理论和结构风险最 ...
- [转]支持向量机SVM总结
首先,对于支持向量机(SVM)的简单总结: 1. Maximum Margin Classifier 2. Lagrange Duality 3. Support Vector 4. Kernel 5 ...
- 机器学习:Python中如何使用支持向量机(SVM)算法
(简单介绍一下支持向量机,详细介绍尤其是算法过程可以查阅其他资) 在机器学习领域,支持向量机SVM(Support Vector Machine)是一个有监督的学习模型,通常用来进行模式识别.分类(异 ...
随机推荐
- 揭秘uc浏览器二
这节,四个议题: ①一个网页显示在webview控件中 ②如何正常隐藏显示标题栏. ③如何用runnable来隐藏标题栏,这样子就更加的专业化. ④上节我们说道了QuickActionGrid,看他长 ...
- PHP 7中利用OpenSSL代替Mcrypt加解密的方法详解
php7.1发布后新特性吸引了不少PHPer,大家都在讨论新特性带来的好处与便利.但是从php7.0 升级到 php7.1 废弃(过时)了一个在过去普遍应用的扩展(mcrypt扩展).官方提供了相应的 ...
- 如何基于TensorFlow使用LSTM和CNN实现时序分类任务
https://www.jiqizhixin.com/articles/2017-09-12-5 By 蒋思源2017年9月12日 09:54 时序数据经常出现在很多领域中,如金融.信号处理.语音识别 ...
- windows无法访问vmware搭建好虚拟机linux web服务器
[前置条件] vmware搭建好虚拟机web服务器 ,但是本机就是无法访问的解决办法. linux虚拟机的网络选择Bridged 桥接到本机网卡. 具体情况如下 : 1.本机能ping通虚拟机 2.虚 ...
- libxml2的安装及使用[总结]
1.前言 xml广泛应用于网络数据交换,配置文件.Web服务等等.近段时间项目中做一些配置文件,原来是用ini,现在改用xml.xml相对来说可视性更为直观,很容易看出数据之间的层次关系.关于xml的 ...
- Kafka:ZK+Kafka+Spark Streaming集群环境搭建(十五)Spark编写UDF、UDAF、Agg函数
Spark Sql提供了丰富的内置函数让开发者来使用,但实际开发业务场景可能很复杂,内置函数不能够满足业务需求,因此spark sql提供了可扩展的内置函数. UDF:是普通函数,输入一个或多个参数, ...
- linux 添加elasticsearch 开机重启(自启动)
在 /etc/init.d 文件夹下建立脚本 eg:data.sh #chkconfig: 2345 80 90#description:auto_run#!bin/bashexport JAVA_H ...
- 什么是哈希码(HashCode)
什么是哈希码(HashCode) 在Java中,哈希码代表对象的特征. 例如对象 String str1 = “aa”, str1.hashCode= 3104 String str2 = “bb”, ...
- C语言代码复习笔记:第二章
输出星星 #include <stdio.h> void printStart( int num ) { ) { printf("*"); }; } int main( ...
- Android [VP]视频播放器播放本地视频时收到短信/彩信,需要界面提示 M
前言 欢迎大家我分享和推荐好用的代码段~~ 声明 欢迎转载,但请保留文章原始出处: CSDN:http://www.csdn.net ...
