25最短路径之Dijkstra算法

图的最优化问题：最小生成树、最短路径

典型的图应用问题

无向连通加权图的最小生成树

有向/无向加权图的最短路径

四个经典算法

Kruskal算法、Prim算法---------------最小生成树

Dijkstra算法、Floyd算法-------------最短路径

单源最短路径问题（单源路径问题）

求某指定顶点（称为源点）到其余各顶点的最短路径问题。

Dijkstra算法

思想：与Prim算法类似，采用路径延伸法。求解过程中，将顶点分成生长点和非生长点

生长点：源点s和已确定最短路径的顶点

非生长点：未确定最短路径的顶点

使用待定路径表

步骤：

步骤1）构造初始待定路径表

对每个非生长点v（共n-1个），定初值：P(v)=sv，D(v)=边<s，v>的长度C<s，v>，如果边<s，v>不存在，则认为其长度为∞。

步骤2）循环n-2遍

①选择最短的待定路径

从待定路径表中选出一条最短的，设其为s到v的路径P(v)，其长度为D(v)，该路径便是s到v的最短路径，v变成为新的生长点。

②修改待定路径表

对剩下的每个非生长点w

设其待定路径为P(w)，长度为D(w)

比较D(w)与D(v)＋C<v，w>的大小，这里的v是新生长点，如果D(w)≤D(v)＋C<v，w>什么也不做，否则，将D(w)改为D(v)＋C<v，w>，同时将P(w)改为P(v)接w，表示从s到v后再到w，比原来从s到w（不过v）更短。

示例

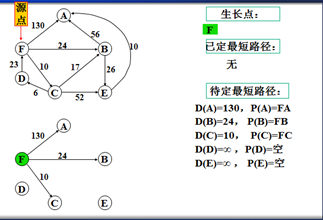
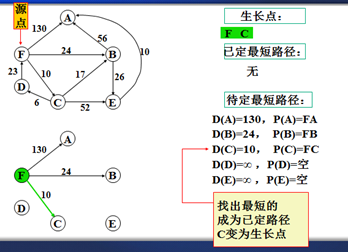
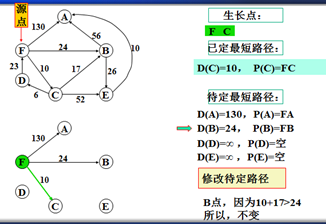
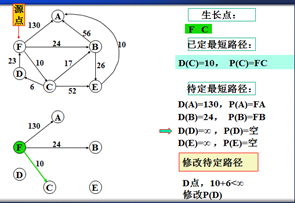
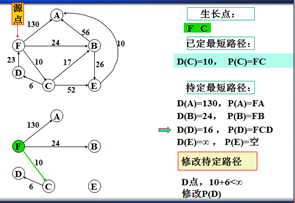
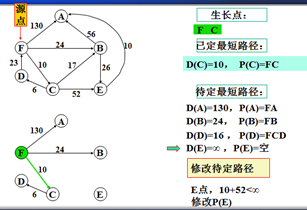
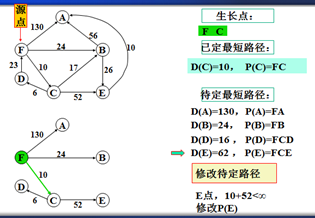
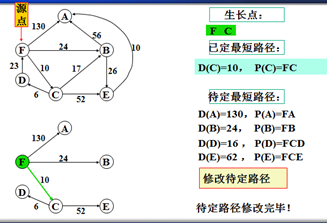
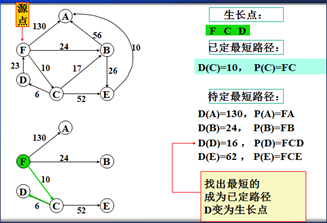
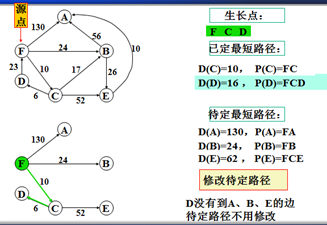
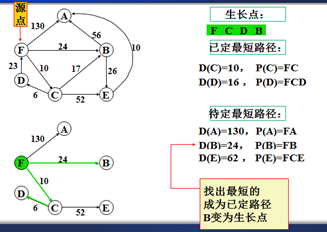
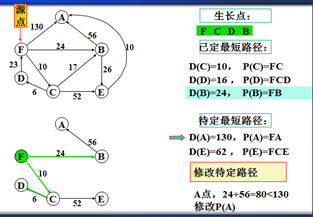
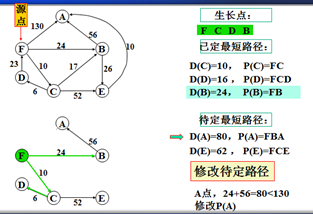
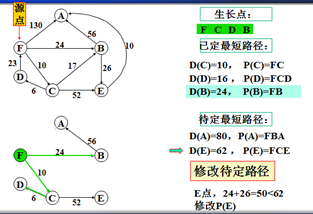
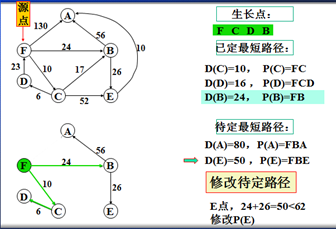
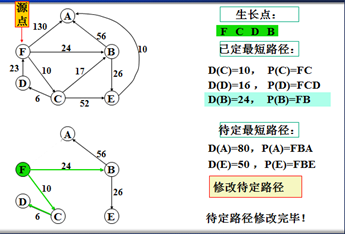
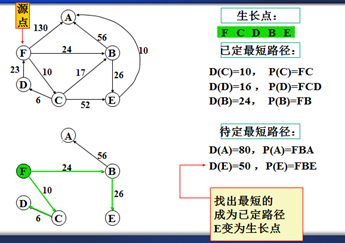
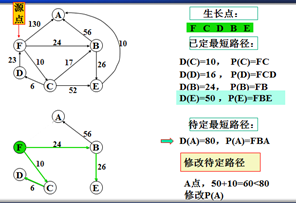
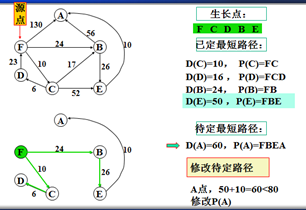
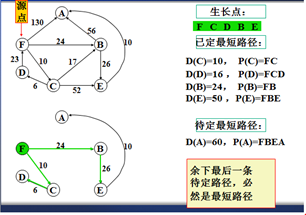
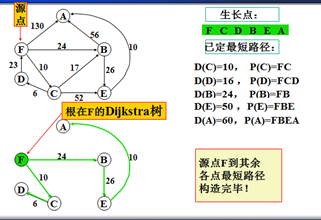
以上是官方示例，Dijkstra算法的实现过程。下面是世俗的观点解析。

1. Dijkstra算法与Prim算法类似，都是利用不断寻找新的生长点。

2.再把新的生长点的路径权值（所经过的路径的权值都要相加）与原生长点路径权值比较。再确定是否替换。

3. Dijkstra算法是有向图，要特别注意方向。

步骤：

1.确定一个源点。即从哪一点开始出发。

2.记录与源点有关的其他结点，且源点为出度。如：F->A、F->B、F->C，注意D->F是以F为入度，所以不记录。

3.观察所以与源点有关的边，选择其中最小权值的边进行遍历，而边的另一个结点作为新的生长点。如：F->A  130、F->B  24、F->C  6，因此选择F->C，则C作为新的生长点。

3.利用深度优先的思想，对C结点的相关结点进行递归。（要注意方向）。

4.直到不能递归的结点。如：D结点。此时要注意：一定要返回源点，源点。不能是C结点。

5.回到源点后，利用广度优先的思想，对源点的其他边再遍历（按权值小到大的方式进行）。

F->B 24 F->A 130，所以选择F->B路径，B作为新的生长点。

6.重复以上步骤。。。。。。。

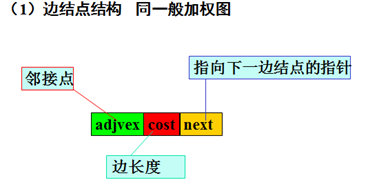
实现Dijkstra算法的存储结构

图可用邻接表存储，结点结构如下：

Dijkstra算法的程序实现

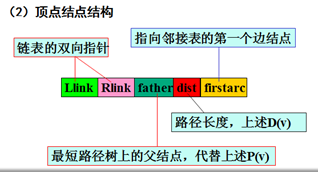
说明：采用“父亲链域法”存储Dijkstra最短路径树

图用邻接表存储，各非生长点的邻接表的表头结点做成带表头监督元结点的双向循环静态链表，兼作待定路径表（便于删除），下标作为顶点序号。

for(v=0; v<=n; v++)

{ L[v].dist=MAXNUM;  //无穷大

L[v].father=s;

L[v].Llink=v-1;     L[v].Rlink=v+1;

}

L[0].Llink=n;

L[n].Rlink=0;  // 以上构造初始链表

L[L[s].Llink].Rlink=L[s].Rlink;

L[L[s].Rlink].Llink=L[s].Llink; //删去源点s

p=L[s].firstarc;

while(p!=NULL)

{ v=p->adjvex;  // v是s的邻接点

L[v].dist=p->cost;

p=p->next;

}