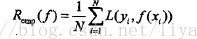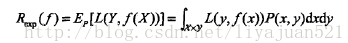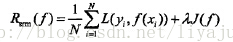机器学习-->期望风险、经验风险与结构风险之间的关系
https://blog.csdn.net/liyajuan521/article/details/44565269
在机器学习中,通常会遇到期望风险、经验风险和结构风险这三个概念,一直不知道这三个概念之间的具体区别和联系,今天来梳理一下:
要区分这三个概念,首先要引入一个损失函数的概念。损失函数是期望风险、经验风险和结构风险的基础。
损失函数是针对单个具体的样本而言的。表示的是模型预测的值与样本真实值之间的差距。比如对于某个样本<Xi,Yi>,其真实的值为Yi,而我们的模型选择决策函数为f,那么通过模型预测的值为f(Xi);损失函数就是用来表示Yi与f(Xi)之间的差距的,我们用函数L(f(Xi),Yi)来衡量。我们希望的是这个L函数最小化。理想的情况是我们的模型决策函数预测值f(Xi)刚好等于该样本的真值Yi。常见的损失函数有以下几种:
现在我们已经清楚了,对于具体的某个样本点,有了衡量其预测值与真实值的差异度的方法了(选取上面任意一个损失函数即可)。
通过损失函数我们只能知道模型决策函数f(X)对于单个样本点的预测能力(借用损失函数L(Y,f(x)),损失函数越小,说明模型对于该样本预测越准确。),那么如果想知道模型f(X)对训练样本中所有的样本的预测能力应该怎么办呢?显然只需所有的样本点都求一次损失函数然后进行累加就好了。如下式
这就经验风险,所谓的经验风险最小化便是让这个式子最小化,注意这个式子中累加和的上标N表示的是训练样例集中样本的数目。
经验风险是对训练集中的所有样本点损失函数的平均最小化。经验风险越小说明模型f(X)对训练集的拟合程度越好,但是对于未知的样本效果怎么样呢?我们知道未知的样本数据(<X,Y>)的数量是不容易确定的,所以就没有办法用所有样本损失函数的平均值的最小化这个方法,那么怎么来衡量这个模型对所有的样本(包含未知的样本和已知的训练样本)预测能力呢?熟悉概率论的很容易就想到了用期望。即假设X和Y服从联合分布P(X,Y).那么期望风险就可以表示为:
这就是期望风险,期望风险表示的是全局的概念,表示的是决策函数对所有的样本<X,Y>预测能力的大小,而经验风险则是局部的概念,仅仅表示决策函数对训练数据集里样本的预测能力。理想的模型(决策)函数应该是让所有的样本的损失函数最小的(也即期望风险最小化),但是期望风险函数往往是不可得到的,即上式中,X与Y的联合分布函数不容易得到。现在我们已经清楚了期望风险是全局的,理想情况下应该是让期望风险最小化,但是呢,期望风险函数又不是那么容易得到的。怎么办呢?那就用局部最优的代替全局最优这个思想吧。这就是经验风险最小化的理论基础。
通过上面的分析可以知道,经验风险与期望风险之间的联系与区别。现在在总结一下:
经验风险是局部的,基于训练集所有样本点损失函数最小化的。
期望风险是全局的,是基于所有样本点的损失函数最小化的。
经验风险函数是现实的,可求的;
期望风险函数是理想化的,不可求的;
只考虑经验风险的话,会出现过拟合的现象,过拟合的极端情况便是模型f(x)对训练集中所有的样本点都有最好的预测能力,但是对于非训练集中的样本数据,模型的预测能力非常不好。怎么办呢?这个时候就引出了结构风险。结构风险是对经验风险和期望风险的折中。在经验风险函数后面加一个正则化项(惩罚项)便是结构风险了。如下式:
相比于经验风险,结构风险多了一个惩罚项,其中
是一个lamada是一个大于0的系数。J(f)表示的是是模型f的复杂度。结构风险可以这么理解:
经验风险越小,模型决策函数越复杂,其包含的参数越多,当经验风险函数小到一定程度就出现了过拟合现象。也可以理解为模型决策函数的复杂程度是过拟合的必要条件,那么我们要想防止过拟合现象的方式,就要破坏这个必要条件,即降低决策函数的复杂度。也即,让惩罚项J(f)最小化,现在出现两个需要最小化的函数了。我们需要同时保证经验风险函数和模型决策函数的复杂度
都达到最小化,一个简单的办法把两个式子融合成一个式子得到结构风险函数然后对这个结构风险函数进行最小化。
机器学习-->期望风险、经验风险与结构风险之间的关系的更多相关文章
- FFMPEG中最要害的结构体之间的关系
FFMPEG中最关键的结构体之间的关系 http://www.myexception.cn/program/1404591.html FFMPEG中结构体很多.最关键的结构体可以分成以下几类: a) ...
- FFMPEG中最关键的结构体之间的关系
FFMPEG中结构体很多.最关键的结构体可以分成以下几类: a) 解协议(http,rtsp,rtmp,mms) AVIOContext,URLProtocol,URLContext主要 ...
- FFmpeg 结构体学习(八):FFMPEG中重要结构体之间的关系
FFMPEG中结构体很多.最关键的结构体可以分成以下几类: 解协议(http,rtsp,rtmp,mms) AVIOContext,URLProtocol,URLContext主要存储视音频使用的协议 ...
- python面向对象与结构成员之间的关系
1面向对象结构分析:----面向对象整体大致分为两块区域:-------第一部分:静态字段(静态变量)部分-------第二部分:方法部分--每个区块可以分为多个小部分 class A: countr ...
- 网络互联技术(2)——前篇—【转载】电脑结构和CPU、内存、硬盘三者之间的关系
原文链接:传送门 详细内容: 电脑结构和CPU.内存.硬盘三者之间的关系 前面提到了,电脑之父——冯·诺伊曼提出了计算机的五大部件:输入设备.输出设备.存储器.运算器和控制器. 我们看一下现在我们电脑 ...
- wordpress数据库结构以及数据表之间的关系
默认WordPress一共有以下11个表.这里加上了默认的表前缀 wp_ . wp_commentmeta:存储评论的元数据 wp_comments:存储评论 wp_links:存储友情链接(Blog ...
- python与C结构体之间二进制数据转换
python与C结构体之间数据转换 前言 在实际应用中,可能会遇到直接和C进行二进制字节流协议通信,这时要把数据解包成python数据,如果可能,最好与C定义的结构体完全对应上. python中有2种 ...
- 电脑结构和CPU、内存、硬盘三者之间的关系
前面提到了,电脑之父——冯·诺伊曼提出了计算机的五大部件:输入设备.输出设备.存储器.运算器和控制器. 我们看一下现在我们电脑的: 键盘鼠标.显示器.机箱.音响等等. 这里显示器为比较老的CRT显示器 ...
- storm中worker、executor、task之间的关系
这里做一些补充: worker是一个进程,由supervisor启动,并只负责处理一个topology,所以不会同时处理多个topology. executor是一个线程,由worker启动,是运行t ...
随机推荐
- 洛谷P4141消失之物
题目描述 ftiasch 有 N 个物品, 体积分别是 W1, W2, …, WN. 由于她的疏忽, 第 i 个物品丢失了. “要使用剩下的 N – 1 物品装满容积为 x 的背包,有几种方法呢?” ...
- j.u.c系列(09)---之并发工具类:CyclicBarrier
写在前面 CyclicBarrier是一个同步辅助类,允许一组线程互相等待,直到到达某个公共屏障点 (common barrier point).因为该 barrier 在释放等待线程后可以重用,所以 ...
- sqlserver2014内存数据库特性介绍
sql server 2014提供了众多激动人心的新功能,但其中我想最让人期待的特性之一就要算内存数据库了,下面就简单介绍一下sql server 2014的内存数据库的一些特性 相信大家对内存数 ...
- Code Fragment-UI加载策略之-可视者优先加载
通常情况 通常程序的UI不太复杂,我们会直接加载这些UI信息 复杂的UI 加载的元素就相对多一些. 加载的数据相对多. 因为UI元素和数据元素都比较多,加载的时间相对多. 可视者优先加载 不是默认的加 ...
- Revit API移动风管
移动风管曲线就可以移动风管 , , ));//向上移动3 ts.Commit(); return Result.Succeeded; } } url:http: ...
- TextAppearance.Material.Widget.Button.Inverse,Widget.Material.Button.Colored
编译xamarin android项目报错: android:TextAppearance.Material.Widget.Button.Inverse android:Widget.Material ...
- AngularJS自定义Directive与controller的交互
有时候,自定义的Directive中需要调用controller中的方法,即Directive与controller有一定的耦合度. 比如有如下的一个controller: app.controlle ...
- ASP.NET MVC与Sql Server交互, 插入数据
在"ASP.NET MVC与Sql Server建立连接"中,与Sql Server建立了连接.本篇实践向Sql Server中插入数据. 在数据库帮助类中增加插入数据的方法. p ...
- Visual Studio 2012使用NUnit单元测试实践01,安装NUnit并使用
在Visual Studio 2012中,默认使用Microsoft自带的MS-Test测试框架.但,Visual Studio同样允许使用第三方测试框架,比如NUnit,xUnit,MbUnit,等 ...
- 解决iframe加载的内容有时显示有时不显示
在ASP.NET MVC项目中遇到了这样的一个问题,假设父页面有一个iframe <iframe id=" width="100%" height="10 ...