洛谷P3389 高斯消元 / 高斯消元+线性基学习笔记

高斯消元

其实开始只是想搞下线性基,,,后来发现线性基和高斯消元的关系挺密切就一块儿在这儿写了好了QwQ

先港高斯消元趴?

这个算法并不难理解啊?就会矩阵运算就过去了鸭,,,

算了都专门为此写个题解还是详细港下趴,,,

就每次选定一个未知数,通过加减消元使得所有方程中只有一个方程中它的系数不为0

然后这么一直做下去最后就会得到一个,这样的东西

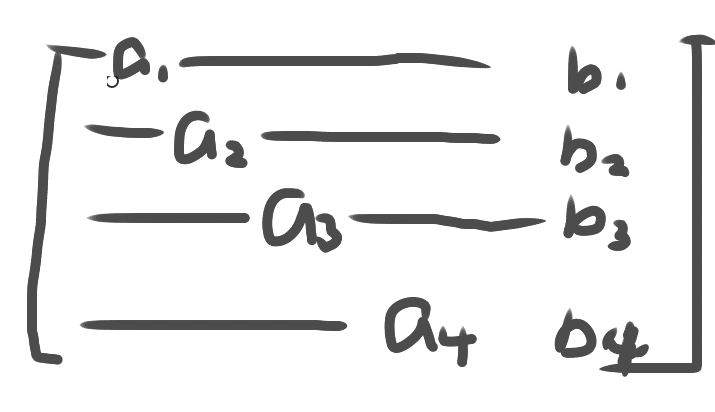
a是系数b是方程右边的那个玩意儿

然后就输出b/a就成了,,还挺简单的是不是x就模拟了一个加减消元

然后就放代码趴

#include<bits/stdc++.h>
using namespace std;
][],inf=1e-;];];
long long read()
{
    ;;
    '))ch=getchar();
    ,ch=getchar();
    )+(x<<)+(ch^'),ch=getchar();
    return y?x:-x;
}
int main()
{
    int n=read();
    ;i<=n;i++);j<=n+;j++)a[i][j]=read();
    ;i<=n;i++)
    {
        ;;
        ;j<=n;j++))mx=fabs(a[j][i]),p=j;
        );
        w[i]=p;pd[p]=;
        ;j<=n;j++)
            ;k<=n+;k++)a[j][k]-=(double)t*a[p][k];}
    }
    ;i<=n;i++)printf(]*1.00000/a[w[i]][i]);
    ;
}

//最近爱上了压行,,,看到以前的代码居然觉得太长了真是看不顺眼x

lq怎么这么蠢啊,,,

umm然后顺便还是注释下,就是,如果不想掉精度的话,在这道题中我是每次消元的时候都精心挑选了一下的都是选的系数最大的,这样精度就掉得少些quqqqqq

但是反正高斯消元也不是重点嘛

今天主要是想研究下

线性基

线性基篇!

线性基的定义,,,看了一个学长的博客,本来一脸懵的现在大概还是懂了点儿quqqqqq

线性基：

　　线性基其实就是构造出一组序列p0,p1...,pn

　　使得从这些数中任选一个子集的异或和的值域同等与从原序列中任选一个子集的异或和的值域。

　　(这里看到另一篇博客中做出了这样的理解:线性基可以算是整个集合的一个压缩)(可以把n个数压缩成二进制中最大位数的个数个)

　　同时保证：pi在二进制下的最高位是2ⁱ

umm其实我觉得定义没有太大的用再了解下性质就可以进入正题辣

线性基有一些性质：

1.线性基的异或集合中不存在0,也就是说,β是V中线性无关的极大子集(因此在高斯消元碰到线性相关题目可以用线性基硬刚x

2.线性基中每个元素的异或方案唯一，也就是说，线性基中不同的异或组合异或出的数都是不一样的(这个与性质1其实是等价的.因为线性无关鸭QwQ←也可以这么想,就是因为不存在0,如果有一样的那再异或一下不就存在0了嘛QAQ

3.线性基的二进制最高位互不相同(因为保证了pi在二进制下的最高位是2ⁱ

4.如果线性基是满的，它的异或集合为[1,2n−1](*这一个点我还没有get呜呜呜

5.线性基中元素互相异或，异或集合不变(因为它是个压缩,能get趴?

然后!有一个我jio得对于线性基特别特别好的解读,我放下QwQ

有一个数集 S，现在可以任取 S 的一个子集，并把这个子集中的所有数异或起来，得到一个新数 t。令所有可行的 t 的集合为 T。线性基可以用于快速确定 T 的信息。
用 n 表示|S|，令 S 中每个元素∈ [0,2^m)
线性基的本质就是高斯消元的矩阵，令 S 中的数为x_1...n,x_i二进制分解后为x_i,0…m−1，如果我们要判断某个数 t 能否被组合，用布尔变量y_i表示是否选择x_i，我们可以列出异或方程组

x_1,0y₁ xor x_2,0y₂ xor ... xor x_n,0y_n = t₀

x_1,1y₁ xor x_2,1y₂ xor ... xor x_n,1y_n = t₁

　　　　　　　　........

x_1,m-1y₁ xor x_2,m-1y₂ xor ... xor x_n,m-1y_n = t_m-1

然后我们可以进行消元，消元之后每一列最多只有一个元素。也就是说，线性基中有贡献的元素个数 k 不超过 m。所以它可以极大地简化一个集合的表示。
因为线性基本质就是高斯消元，所以判断 t 能否被凑出,只要按照高斯消元求解的方法，依次确定每一位即可。
同时，由于每一列最多一个元素，所以线性基中的 k 个元素是互不影响的，那么集合 S 能够异或出的不同的数的个数就为2^k

然后就港下操作和应用好了quqqqqq

应用的话目前学到了的有三种:

　　首先最直接的可以用来高斯消元处理线性相关

　　然后还可以求,第k大

　　然后求异或和最大的时候用它可以按位贪心了

umm然后港下它滴实现?

构造:

直接对读入的数二进制地从前往后扫

如果扫到一个位置是1就判断一下,如果已经有这一位是1的数了就异或一下这个最高位是1的数(为了维护性质&定义)

如果没有最高位这里是1的数就放进去并停止扫描

然后就成功构造完成辣!

可以发现这样的话我们放入一个数就只会有俩结果

第一个,能扫到,于是在过程中就会被放进去并停止扫描

第二个,一直到了最后它变成0就退出了,这就说明它是能被表示出来的了(就可以把所有把它的有1的位数作为最高位的线性基异或起来就能表示出来,get?

,){<<i)){if(!p[i] ){p[i]=x;return;}x^=p[i];}}}

还是,放下代码趴

合并:

线性基的合并就直接合并就好了鸭,放下代码QwQ

xxj merg(xxj gd,xxj gs){my(i,,)if(!gd.p[i])gs.inst(gd.p[i]);return gs;}

这儿是代码QwQ

查询是否能表示出:

再插入那一段中我们港,如果它变成0说明它可以表示出来了,所以我们就能get辣,直接insert操作修改一下就欧克

查询max:

两种,分别港下QwQ

第一个是可以直接每次判断异或这个基底之后会不会变大,会就异或就欧克

另一种因为和后面那个第K大一块儿说所以看后面趴QAQ

查询第k大:

这里还是有一点儿小技巧的趴,,,

就构造完线性基之后对它rebuild的一下,使得每一位最多有一个数为1

具体的实现就跟高斯消元似的搞下就好

然后假如当前位为1,且后面有cnt位,显然比它小的就是有2^cnt个(0这种细节什么的特殊考虑下就好,,,

然后就欧克了,也放下代码趴QwQ

il ,)my(j,i-,)<<j))q[i]^=q[j];rp(i,,)if(q[i])p[++cnt]=q[i];}
il void query()
{
    ll x=rd();<<(cnt+)))return void(printf("-1\n"));
    ll ;my(i,cnt,)<<i))as^=p[i];return void(printf("%lld\n",as));
}

最后放下题单,,,都是些比较基础的,只有线性基的知识点的题目QwQ

(有几个[x]的链接是题解,,,其他的是题目QwQ

[X] 线性基模板

[X] 元素

[X] 新Nim游戏

[X] 最大XOR和路径

[X] 幸运数字

[ ] 玛里苟斯

[ ] albus就是要第一个出场

[X] XOR