LeetCode刷题总结-数组篇（下）

本期讲O(n)类型问题，共14题。3道简单题，9道中等题，2道困难题。数组篇共归纳总结了50题，本篇是数组篇的最后一篇。其他三个篇章可参考：

• LeetCode刷题总结-数组篇（上），子数组问题（共17题）
• LeetCode刷题总结-数组篇（中），矩阵问题（共12题）
• LeetCode刷题总结-数组篇（番外），思维转换类型问题（共7题）

本系列50道题是作者在LeetCode题库数组标签中包含的202道题中，按照解答考点分类归纳总结的题型。解法仅供参考，主要在于题目和考点的分类。希望对准备刷LeetCode，而感觉题目繁多、标签太多、时间较少，不知道从何开始刷题的同学一点小小的帮助^~^，也是自己后期二刷的资料吧（PS：如果有时间的话）。

O(n)类型问题，是指要求算法的时间复杂度为O(n)。这类题目的特点是题意一般比较容易理解，而且其暴力求解的方案也比较容易想到。但是，题目确要求你不能采用暴力法求解，这往往是考察我们对双指针、快慢指针、动态规划、哈希数组和特定数学思想的应用。

在双指针方面，一般基础的策略是采用空间换取时间的策略。即先采用一个数组从原数组右边开始遍历，保存当前更新的临时变量。最后，从数组的左边开始依次遍历，不断更新最终的结果。此思路的应用，可以参考例9、例10和例11。

另外，双指针的应用解法也可以在O(1)的空间复杂度里面实现，采用一个临时变量随着遍历不断更新当前状态，夹杂着动态规划的思想。这类考点的应用，可以参考例5和例12。

在数学思维考察方面，组合数学的知识应用也是比较常见。比如考察对组合数学中字典序求解的应用，可以参考例1。数学中正负数转换为数组下标的思想，可以参考例2、例6。快速找到当前示例的数学规律，归纳出递推公式，可以参考例8、例13。

例3是一道非常经典的面试题，题目有多种解法，本文中给出是采用三次翻转求得最终结果的解法。在矩阵应用中，利用翻转操作一般也可以取得令人惊奇的效果。活用翻转也是一种技巧。

例4则是让人感叹的解法。采用摩尔投票法寻找数组中最多的元素。该思维应该可以归纳为寻找最多元素的一种特解思路。

在数组哈希思路的应用方面，可以参考例7和例14，是很典型的以空间换取时间的例题。

例1 下一个排列

题号：31，难度：中等

题目描述：

解题思路：

本题需要注意的关键点：原地修改，字典序。此题的解答用到了组合数学的知识，寻找比当前序列大的最小字典序。即从该序列尾部开始遍历，直到当前元素（假设位置为i）比该元素前面的元素大的时候停止。然后从i道最后一个元素序列中找到比第i-1个元素大的最小元素进行交换，最后把最后i个元素从小到大排序即可。

具体代码：

class Solution {
    public void nextPermutation(int[] nums) {
        int i = nums.length - 2;
        while(i >= 0 && nums[i] >= nums[i+1])
            i--;
        if(i >= 0) {
            int j = nums.length - 1;
            while(nums[j] <= nums[i])
                j--;
            int temp = nums[i];
            nums[i] = nums[j];
            nums[j] = temp;
            reverse(nums, i+1, nums.length - 1);
        } else {
            reverse(nums, 0, nums.length-1);
        }
    }

    public void reverse(int[] nums, int i, int j) {
        while(i < j) {
            int temp = nums[i];
            nums[i++] = nums[j];
            nums[j--] = temp;
        }
    }
}

执行结果：

例2 缺失的第一个正数

题号：41，难度：困难

题目描述：

解题思路：

此题虽然被划分为困难题，实际上比较简单。题目要求是没有出现的最小正整数，那么返回的结果最大值只能是数组长度加1，最小值是1。那么只需要利用原有数组，把其中小于等于0的数字标记为大于数组长度*2的元素，剩下的把在1到数组长度之间的元素采用数组的下标元素取负数表示。最后，从数组第一个元素开始遍历，一旦出现大于0的元素，那么该元素下标即为最终结果。

具体代码：

class Solution {

    public int firstMissingPositive(int[] nums) {
        int len = nums.length * 2;
        for(int i = 0;i < nums.length;i++) {
            if(nums[i] <= 0)
                nums[i] = len++;
        }

        int j = 0;
        for(;j < nums.length;j++) {
            if(Math.abs(nums[j]) <= nums.length && nums[Math.abs(nums[j]) - 1] > 0)
                nums[Math.abs(nums[j]) - 1]  *= -1;
        }
        for(j = 0;j < nums.length;j++) {
            if(nums[j] > 0)
                break;
        }

        return j + 1;
    }

}

执行结果：

例3 旋转数组

题号：189，难度：简单

题目描述：

解题思路：

采用三次翻转操作。第一次将整个数组翻转一次，第二次将要右移的前K个元素翻转一次，第三次将剩余的k-n-1个元素翻转一次。最终得到的结构即为目标值。

具体代码：

class Solution {
    public void rotate(int[] nums, int k) {
        int n = nums.length;
        k %= n;
        reverse(nums, 0, n - 1);
        reverse(nums, 0, k - 1);
        reverse(nums, k, n - 1);
    }

    private void reverse(int[] nums, int start, int end) {
        while (start < end) {
            int temp = nums[start];
            nums[start++] = nums[end];
            nums[end--] = temp;
        }
    }
}

执行结果：

例4 求众数II

题号：229，难度：中等

题目描述：

解题思路：

采用摩尔投票法，具体就是遇到相等的数，统计该数的个数自动加1，否则自动减一，一旦减到0后，更换当前存储的数字。摩尔投票法首次运用的题是求一维数组中数目超过一半的数（具体可参考题目：求众数， 题号169, 难度：简单）。本题稍作变换即可，开启两个变量计数和存储当前的数。开启两个数的数学意义在于，一个数组最多只能有两个数超过数组的三分之一。

具体代码：

class Solution {

    public List<Integer> majorityElement(int[] nums) {
        List<Integer> result = new ArrayList<>();  //摩尔投票法
        int count1 = 0, temp1 = 0;
        int count2 = 0, temp2 = 0;
        for(int i = 0;i < nums.length;i++) {
            if((count1 == 0 || temp1 == nums[i]) && temp2 != nums[i]) {
                count1++;
                temp1 = nums[i];
            } else if(count2 == 0 || temp2 == nums[i]) {
                count2++;
                temp2 = nums[i];
            } else{
                count1--;
                count2--;
            }
        }

        count1 = 0;
        count2 = 0;
        for(int i = 0;i < nums.length;i++) {
            if(nums[i] == temp1)
                count1++;
            else if(nums[i] == temp2)
                count2++;
        }
        if(count1 > nums.length / 3)
            result.add(temp1);
        if(temp1 != temp2 && count2 > nums.length / 3)
            result.add(temp2);

        return result;
    }

}

执行结果：

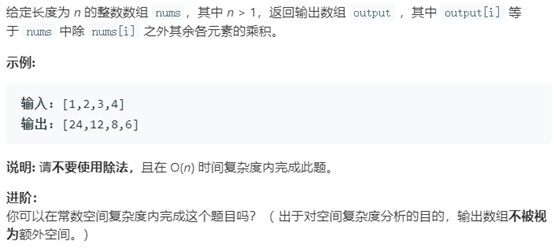
例5 除自身以外数组的乘积

题号：238，难度：中等

题目描述：

解题思路：

以空间换时间的策略，从数组左边依次遍历，保存连续乘积；然后，从数组右边依次遍历，保存连续乘积。最后，从数组第一数字开始遍历，取该数组左边的连续乘积和右边的连续乘积相乘即可。时间复杂度为O(n)，空间复杂度为O(n)。

进阶如何使得空间复杂度为O(1)呢？即采用常数空间保存左边连续乘积，和右边连续乘积即可。这里感觉采用了动态规划的思路来临时保存左右连续乘积。

具体代码：

class Solution {

    public int[] productExceptSelf(int[] nums) {
        int[] result = new int[nums.length];
        int left = 1;
        int right = 1;

        for(int i = 0;i < nums.length;i++) {
            result[i] = left;
            left *= nums[i];
        }

        for(int i = nums.length - 1;i >= 0;i--) {
            result[i] *= right;
            right *= nums[i];
        }

        return result;
    }
}

执行结果：

例6 数组中重复的数据

题号：442，难度：中等

题目描述：

解题思路：

此题采用数组下标来判定出现两次的元素。题目中表明1 <= a[i] <= n，那么出现两次的元素i，对应下标i -1，出现一次时使得a[i - 1] * -1，当再次出现a[i - 1]小于零时，那么i就出现了两次。

具体代码：

class Solution {

    public List<Integer> findDuplicates(int[] nums) {
        List<Integer> result = new ArrayList<>();
        for(int i = 0;i < nums.length;i++) {
            int j = Math.abs(nums[i]) - 1;
            if(nums[j] < 0)
                result.add(j + 1);
            else
                nums[j] *= -1;
        }

        return result;
    }
}

执行结果：

例7 数组拆分I

题号：561，难度：简单

题目描述：

解题思路：

题目中有说明元素的范围，且比较小。观察示例的数据发现，只需要对数据进行从小到大排序，依次选取两个元素中第一个元素作为最终结果的一部分即可。此时，可以采取数据哈希的思路来完成数据的排序操作，时间复杂度为O(n)。

具体代码：

class Solution {

    public int arrayPairSum(int[] nums) {
        int[] temp = new int[20001];
        for(int i = 0;i < nums.length;i++) {
            int j = nums[i] + 10000;
            temp[j]++;
        }

        int result = 0;
        for(int i = 0;i < temp.length;i++) {
            if(temp[i] > 0) {
                int a = i - 10000;
                temp[i]--;
                while(i < temp.length && temp[i] <= 0) {
                    i++;
                }
                // if(i < temp.length)
                //     System.out.println("i = "+i+", temp[i] = "+temp[i]);
                if(i < temp.length) {
                    result += a;
                    temp[i]--;
                }
                if(temp[i] > 0)
                    i--;
            }
        }

        return result;
    }
}

执行结果：

例8 优美的排列II

题号：667，难度：中等

题目描述：

解题思路：

此题考察我们寻找数学规律。先从1到k存储每个元素，然后从k+1开始每两个数存储(n--, k++)即可。

具体代码：

class Solution {

    public int[] constructArray(int n, int k) {
        int[] result = new int[n];
        int temp = 1;
        for(int i = 0;i < n - k;i++)
            result[i] = temp++;
        int count = n;
        boolean judge = true;
        for(int i = n - k;i < n;i++) {
            if(judge) {
                result[i] = count--;
                judge = false;
            } else {
                result[i] = temp++;
                judge = true;
            }
        }

        return result;
    }
} 

执行结果：

例9 最多能完成排序的块 II

题号：768，难度：困难

题目描述：

解题思路：

此题考察双指针和动态规划思想的应用。双指针，从右边依次遍历存储当前的最小值。从左边开始依次遍历，存储当前的最大值。如果左边当前的最大值小于等于右边的最小值，则可以分割为一个块。

具体代码：

class Solution {

    public int maxChunksToSorted(int[] arr) {
        int[] right_min = new int[arr.length];
        for(int i = arr.length - 1;i >= 0;i--) {
            if(i == arr.length - 1)
                right_min[i] = arr[i];
            else
                right_min[i] = Math.min(arr[i], right_min[i+1]);
        }

        int result = 1;
        int left_max = 0;
        for(int i = 0;i < arr.length - 1;i++) {
            if(arr[left_max] <= right_min[i + 1]) {
                result++;
                left_max = i + 1;
            } else {
                if(arr[left_max] < arr[i])
                    left_max = i;
            }
        }

        return result;
    }
} 

执行结果：

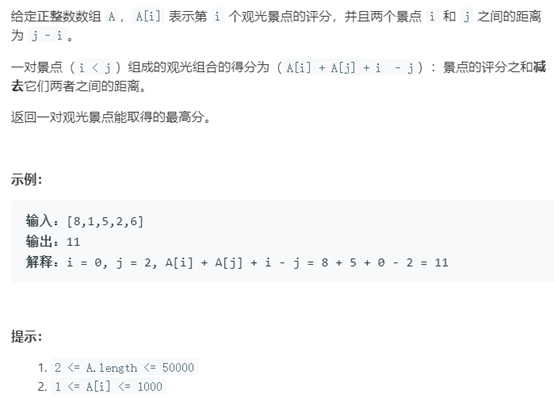
例10 最佳观光组合

题号：1014，难度：中等

题目描述：

解题思路：

此题是一个双指针和动态规划思想的应用。可以把得分拆为两个部分，左边遍历，寻找max(A[i] + i)；右边遍历，寻找max(A[j] - j)。可以采用一个数组保存右边最大值，让后从左边开始遍历，不断更新最终的最大值。

具体代码：

class Solution {

    public int maxScoreSightseeingPair(int[] A) {
        int[] right_max = new int[A.length];
        for(int i = A.length - 1;i >= 0;i--) {
            if(i == A.length - 1)
                right_max[i] = A[i] - i;
            else
                right_max[i] = Math.max(A[i] - i, right_max[i+1]);
        }
        int result = 0;
        for(int i = 0;i < A.length - 1;i++)
            result = Math.max(result, A[i] + i + right_max[i+1]);

        return result;
    }
}

执行结果：

例11 到最近的人的最大距离

题号：849，难度：简单

题目描述：

解题思路：

此题考察我们双指针的思想应用。可以采用一个指针从右边依次遍历，存储到当前元素的连续零的个数（此处需要注意尾部全为零的特殊情况）。然后，从左边开始遍历，计算左边连续零的个数，最后比较左边和右边零个数的大小即可。

具体代码：

class Solution {

    public int maxDistToClosest(int[] seats) {
        int[] right = new int[seats.length];
        for(int i = seats.length - 1;i >= 0;i--) {
            if(i == seats.length - 1) {
                right[i] = seats[i] == 1 ? 0 : 1;
            } else if(seats[i] == 0){
                right[i] = 1 + right[i+1];
            }
        }
        int result = 0, left = seats.length;
        for(int i = 0;i < seats.length;i++) {
            // System.out.println("i = "+i+", left = "+left+", right = "+right[i]+", result = "+result);
            if(seats[i] == 1)
                left = 1;
            else {
                int temp = left;
                if(right[i] < left && right[i] + i < seats.length)
                    temp = right[i];
                result = Math.max(result, temp);
                left++;
            }
        }

        return result;
    }
} 

执行结果：

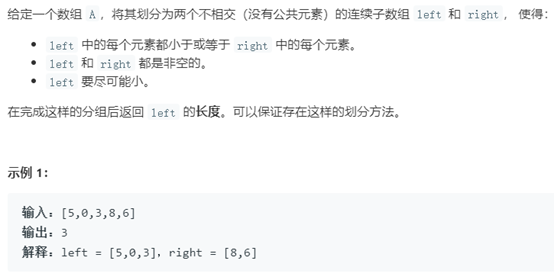
例12 分割数组

题号：915，难度：中等

题目描述：

解题思路：

此题同样是双指针思路的应用，但是可采用当前最大值和左数组最大值的思想来做。

具体代码：

class Solution {
    public int partitionDisjoint(int[] A) {
        int[] right_min = new int[A.length];
        for(int i = A.length - 1;i >= 0;i--) {
            if(i == A.length - 1)
                right_min[i] = A[i];
            else
                right_min[i] = Math.min(A[i], right_min[i+1]);
        }
        int result = 0, left_max = A[0];
        for(;result < A.length - 1;result++) {
            left_max = Math.max(A[result], left_max);
            if(left_max <= right_min[result + 1])
                break;
        }

        return result + 1;
    }

    /* 当前最大值和左边最大值
    public int partitionDisjoint(int[] A) {
        if (A == null || A.length == 0) {
            return 0;
        }

        int leftMax = A[0];
        int max = A[0];
        int index = 0;

        for (int i = 0; i < A.length; i++) {
            max = Math.max(max, A[i]);
            if(A[i] < leftMax) {
                leftMax = max;
                index = i;
            }
        }

        return index + 1;
    } */
}

执行结果：

例13 将字符串翻转到单调递增

题号：926， 难度：中等

题目描述：

解题思路：

此题考察我们的数学思维。统计从左到右遍历时0的个数和1的个数，一旦零的个数大于1，结果自动增加1的个数，同时把0和1的个数置零，从新开始统计。

具体代码：

class Solution {
    /*
    * 某一位为1时，前面一位是0或者1都可以
    * 某一位为0时，前面一位只能为0
    */
    public int minFlipsMonoIncr(String S) {
        int zero = 0, one = 0;
        int result = 0;
        for(char s: S.toCharArray()){
            if(s == '0')
                zero++;
            else
                one++;
            if(zero > one) {
                result += one;
                zero = 0;
                one = 0;
            }
        }
        result += zero;

        return result;
    }
}

执行结果：

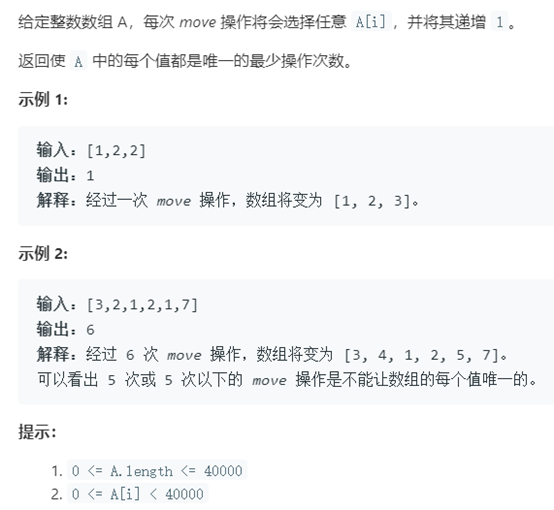
例14 使数组唯一的最小增量

题号：945，难度：中等

题目描述：

 

解题思路：

此题提示说明，0 <= A[i] < 40000。可知可以采用数组哈希的思想来求解本题，以空间换时间的思想，最终的时间复杂度为O(n)。

具体代码：

class Solution {

    public int minIncrementForUnique(int[] A) {
        int[] value_A = new int[41000];
        for(Integer a: A)
            value_A[a]++;
        int result = 0;
        for(int i = 0;i < A.length;i++) {
            if(value_A[A[i]] == 1)
                continue;
            int temp = A[i];
            int count = 0;
            while(value_A[temp] > 1) {
                value_A[temp]--;
                while(value_A[A[i]] > 0) {
                    count++;
                    A[i]++;
                }
                value_A[A[i]]++;
                result += count;
            }
        }

        return result;
    }
}

执行结果：