JavaScript图形实例：合成花卉图

我们知道在直角坐标系中，圆的方程可描述为：

X=R*COS(α)

Y=R*SIN(α)

用循环依次取α值为0~2π，计算出X和Y,在canvas画布中将坐标点（X,Y）用线连起来，可绘制出一个圆。编写HTML文件内容如下：

<!DOCTYPE html>

<head>

function draw(id)

{

var canvas=document.getElementById(id);

if (canvas==null)

return false;

var context=canvas.getContext('2d');

context.fillStyle="#EEEEFF";

context.fillRect(0,0,400,300);

context.strokeStyle="red";

context.lineWidth=2;

var dig=Math.PI/180;

context.beginPath();

var r=100;

for (var i=0;i<=360;i++)

{

x=200+r*Math.cos(i*dig);

y=150+r*Math.sin(i*dig);

if (i==0)

{

context.moveTo(x,y);

bx=x; by=y;

}

else

context.lineTo(x,y);

}

context.lineTo(bx,by);

context.closePath();

context.stroke();

}

</script>

</head>

<canvas id="myCanvas" width="400" height="300">您的浏览器不支持canvas！

</canvas>

</body>

</html>

将上述HTML代码保存到一个html文本文件中，再在浏览器中打开包含这段HTML代码的html文件，可以看到在浏览器窗口中绘制出如图1所示的圆。

图1 圆的绘制

1．圆和正弦波合成的花卉图

先在HTML页面中设置一个画布。

</canvas>

再在定义的这块400*300的canvas（画布）上面用循环（0~2π）绘制圆和正弦波合成的花卉图。

绘制图案的基本思想是：将圆的方程与一个正弦波进行迭加，即设立坐标计算公式为：

X=R*COS(α)*（0.5+SIN(6α)/2）

Y=R*SIN(α) *（0.5+SIN(6α)/2）

再用循环依次取α值为0~2π，计算出X和Y,在canvas画布中将坐标点（X,Y）用线连起来，可绘制出一个封闭曲线图形，然后将该图形填充颜色，可得到一个花卉图案。

可编写如下的HTML代码。

<!DOCTYPE html>

<head>

<title>圆和正弦波合成的花卉图</title>

function draw(id)

{

var canvas=document.getElementById(id);

if (canvas==null)

return false;

var context=canvas.getContext('2d');

context.fillStyle="#EEEEFF";

context.fillRect(0,0,400,300);

context.fillStyle="red";

context.strokeStyle="white";

context.lineWidth=2;

var dig=Math.PI/180;

context.beginPath();

var r=100;

for (var i=0;i<=360;i++)

{

c=r*(1/2.0+Math.sin(6*i*dig)/2);

x=200+c*Math.cos(i*dig);

y=150+c*Math.sin(i*dig);

if (i==0)

{

context.moveTo(x,y);

bx=x; by=y;

}

else

context.lineTo(x,y);

}

context.lineTo(bx,by);

context.closePath();

context.stroke();

context.fill();

}

</script>

</head>

<canvas id="myCanvas" width="400" height="300">您的浏览器不支持canvas！

</canvas>

</body>

</html>

将上述HTML代码保存到一个html文本文件中，再在浏览器中打开包含这段HTML代码的html文件，可以看到在浏览器窗口中绘制出如图2所示的圆和正弦波合成的花卉图。

图2 圆和正弦波合成的花卉图

2．可设置合成方式的圆和正弦波合成花卉图

在上面的代码中，语句“c=r*(1/2.0+Math.sin(6*i*dig)/2);”中的6表示绘制的花卉图案的花瓣数目，0.5（1/2）表示将圆和正弦波合成时，圆所占的比例，如果修改这两个值，将绘制出不同的花卉图案。

我们可以在浏览器窗口中定义一个表单，通过表单可以设置花瓣数目，还可以设置圆和正弦波合成时的比例，这样输入相应参数值后，再单击“确定”按钮绘制合成花卉图案。

编写HTML文件如下。

<!DOCTYPE html>

<head>

<title>可设置合成方式的圆和正弦波合成花卉图</title>

function draw(id)

{

var canvas=document.getElementById(id);

if (canvas==null)

return false;

var context=canvas.getContext('2d');

context.fillStyle="#EEEEFF";

context.fillRect(0,0,500,300);

context.fillStyle="red";

context.strokeStyle="white";

context.lineWidth=2;

var dig=Math.PI/180;

context.beginPath();

var r=100;

var n=eval(document.myForm.petalNum.value);

var a=eval(document.myForm.circle.value);

var b=eval(document.myForm.sineWave.value);

var prop=a/(a+b);

for (var i=0;i<=360;i++)

{

c=r*(prop+(1-prop)*Math.sin(n*i*dig));

x=250+c*Math.cos(i*dig);

y=150+c*Math.sin(i*dig);

if (i==0)

{

context.moveTo(x,y);

bx=x; by=y;

}

else

context.lineTo(x,y);

}

context.lineTo(bx,by);

context.closePath();

context.stroke();

context.fill();

}

</script>

</head>

<body>

花瓣数<input type=number name="petalNum" value=6 size=2>

合成比例 &nbsp圆：正弦波=<input type=number name="circle" value=1 size=2>：<input type=number name="sineWave" value=1 size=2>

</form><br>

<canvas id="myCanvas" width="500" height="300">您的浏览器不支持canvas！

</canvas>

</body>

</html>

在浏览器中打开包含这段HTML代码的html文件，在表单的“花瓣数”数字框中输入“20”，“合成比例”对应的两个数字框中输入“1”和“1”，单击“确定”按钮，可以看到在浏览器窗口中绘制出如图3所示的20瓣花卉图案。若在表单的“花瓣数”数字框中输入“8”，“合成比例”对应的两个数字框中输入“2”和“10”，单击“确定”按钮，可以看到在浏览器窗口中绘制出如图4所示的8瓣花卉图案。

图3 20瓣花卉图案

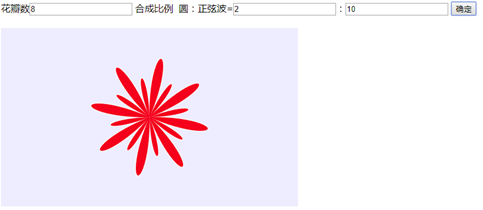
图4 8瓣花卉图案

3．圆和三次谐波合成的花卉图

前面是将圆的方程与一个正弦波进行迭加，若将一个圆与一个三次谐波合成，可设立坐标计算公式为：

X=R*（1+SIN(3*6α)/5）*（0.5+SIN(6α)/2）*COS(α)

Y=R*（1+SIN(3*6α)/5）*（0.5+SIN(6α)/2）*SIN(α)

完整的HTML代码如下。

<!DOCTYPE html>

<head>

<title>圆和三次谐波合成的花卉图</title>

function draw(id)

{

var canvas=document.getElementById(id);

if (canvas==null)

return false;

var context=canvas.getContext('2d');

context.fillStyle="#EEEEFF";

context.fillRect(0,0,400,300);

context.fillStyle="red";

context.strokeStyle="white";

context.lineWidth=2;

var dig=Math.PI/180;

context.beginPath();

var r=100;

for (var i=0;i<=360;i++)

{

b=r+r/5*Math.sin(3*6*i*dig);

c=b*(1/2.0+Math.sin(6*i*dig)/2);

x=200+c*Math.cos(i*dig);

y=150+c*Math.sin(i*dig);

if (i==0)

{

context.moveTo(x,y);

bx=x; by=y;

}

else

context.lineTo(x,y);

}

context.lineTo(bx,by);

context.closePath();

context.stroke();

context.fill();

}

</script>

</head>

<canvas id="myCanvas" width="400" height="300">您的浏览器不支持canvas！

</canvas>

</body>

</html>

在浏览器中打开包含这段HTML代码的html文件，可以看到在浏览器窗口中绘制出如图5所示的圆和三次谐波合成的花卉图。

图5 圆和三次谐波合成的花卉图

若将合成计算式中的（1+SIN(3*6α)/5）改写为（1+SIN(5*6α)/5），也就是将语句“b=r+r/5*Math.sin(3*6*i*dig);”改写为“b=r+r/5*Math.sin(5*6*i*dig);”，再在浏览器中打开修改后的html文件，可以看到在浏览器窗口中绘制出如图6所示的圆和五次谐波合成的花卉图。

图6 圆和五次谐波合成的花卉图

4．圆和三次谐波合成的不同花瓣数的花卉图

在与三次谐波进行合成时，同样可以设置花卉的花瓣数目。可以编写HTML文件如下。

<!DOCTYPE html>

<head>

<title>圆和三次谐波合成不同花瓣数的花卉图</title>

function draw(id)

{

var canvas=document.getElementById(id);

if (canvas==null)

return false;

var context=canvas.getContext('2d');

context.fillStyle="#EEEEFF";

context.fillRect(0,0,300,300);

context.fillStyle="red";

context.strokeStyle="white";

context.lineWidth=2;

var dig=Math.PI/180;

context.beginPath();

var r=50;

for (var n=2;n<=10;n++)

{

var offsetx=(n-2)%3*100+50;

var offsety=((n-1)%3!=0?Math.floor((n-1)/3):(n-1)/3-1)*100+50;

for (var i=0;i<=360;i++)

{

b=r+r/5*Math.sin(3*n*i*dig);

c=b*(1/2.0+Math.sin(n*i*dig)/2);

x=offsetx+c*Math.cos(i*dig);

y=offsety+c*Math.sin(i*dig);

if (i==0)

{

context.moveTo(x,y);

bx=x; by=y;

}

else

context.lineTo(x,y);

}

context.lineTo(bx,by);

context.closePath();

context.stroke();

context.fill();

}

</script>

</head>

<canvas id="myCanvas" width="300" height="300">您的浏览器不支持canvas！

</canvas>

</body>

</html>

在浏览器中打开包含这段HTML代码的html文件，可以看到在浏览器窗口中绘制出如图7所示的圆和三次谐波合成不同花瓣数的花卉图。图中花卉的花瓣数分别为2~9。

图7 圆和三次谐波合成不同花瓣数的花卉图