[Pandas] 01 - A guy based on NumPy
主要搞明白NumPy “为什么快”？
一、学习资源
- Panda 中文
- 易百教程
- 远程登录Jupyter笔记本
- "第六章、矩阵和矢量计算" from《Python高性能编程》
- 系统级性能分析工具perf的介绍与使用
二、效率进化
NumPy 底层进行了不错的优化。
In [11]:
loops = 25000000
from math import *
# 策略1：对每一个元素依次进行计算
a = range(1, loops)
def f(x):
return 3 * log(x) + cos(x) ** 2
%timeit r = [f(x) for x in a]
1 loop, best of 3: 14.4 s per loop
In [12]:
# 策略2：使用np import numpy as np
a = np.arange(1, loops)
%timeit r = 3 * np.log(a) + np.cos(a) ** 2
10 loops, best of 3: 1.94 s per loop
In [13]:
# 策略3：numexpr方法，避免了数组在内存中复制 import numexpr as ne
ne.set_num_threads(1)
f = '3 * log(a) + cos(a) ** 2'
%timeit r = ne.evaluate(f)
10 loops, best of 3: 373 ms per loop
In [14]:
# 策略4：再并发四线程
ne.set_num_threads(4) # 支持并发
%timeit r = ne.evaluate(f)
100 loops, best of 3: 195 ms per loop
三、高级知识点
(a) numexpr
NumPy 虽然通过底层高度优化过的计算库可以实现接近C的高效计算，但在计算复杂且计算量庞大的时候多少还是有些嫌慢。Numexpr 库是最近发现的一个非常简单易用的 Numpy性能提升工具。
Goto: NumExpr: Fast numerical expression evaluator for NumPy
(b) cupy利用gpu加速
先安装cuda驱动：[CUDA] 00 - GPU Driver Installation & Concurrency Programming
再安装CuPy驱动：CuPy Installation
(c) PyPy 与 CPython
需要了解：PyPy和CPython的不同点。
CPython的思路
def add(x, y):
return x + y if instance_has_method(x, '__add__') {
return call(x, '__add__', y) // x.__add__ 里面又有一大堆针对不同类型的 y 的判断
} else if isinstance_has_method(super_class(x), '__add__' {
return call(super_class, '__add__', y)
} else if isinstance(x, str) and isinstance(y, str) {
return concat_str(x, y)
} else if isinstance(x, float) and isinstance(y, float) {
return add_float(x, y)
} else if isinstance(x, int) and isinstance(y, int) {
return add_int(x, y)
} else ...
Just In Time 编译
为何加速了呢？PyPy 执行的时候，发现执行了一百遍 add 函数，发现你 TM 每次都只传两个整数进来，那我何苦每次还给你做这么多计算。于是当场生成了一个类似 C 的函数：
int add_int_int(int x, int y) {
return x + y;
}
系统级性能剖析
一、原始实验
原始代码，作为之后的优化参照。
import numpy as np
import time grid_size = (512,) def laplacian(grid, out):
np.copyto(out, grid)
np.multiply(out, -2.0, out)
np.add(out, np.roll(grid, +1), out)
np.add(out, np.roll(grid, -1), out) def evolve(grid, dt, out, D=1):
laplacian(grid, out)
np.multiply(out, D * dt, out)
np.add(out, grid, out)
def run_experiment(num_iterations):
scratch = np.zeros(grid_size)
grid = np.zeros(grid_size) block_low = int(grid_size[0] * .4)
block_high = int(grid_size[0] * .5)
grid[block_low:block_high] = 0.005 start = time.time()
for i in range(num_iterations):
evolve(grid, 0.1, scratch)
grid, scratch = scratch, grid
return time.time() - start
if __name__ == "__main__":
run_experiment(500)
性能分析一：
$ sudo perf stat -e cycles,stalled-cycles-frontend,stalled-cycles-backend,instructions,cache-references,cache-misses,branches,branch-misses,task-clock,faults,minor-faults,cs,migrations -r 3 python diffusion_python_memory.py
Performance counter stats for '/usr/local/anaconda3/bin/python3 diffusion_numpy_memory.py' ( runs):
cycles # 3.605 GHz ( +- 2.30% ) (65.11%)
<not supported> stalled-cycles-frontend
<not supported> stalled-cycles-backend
instructions # 1.27 insn per cycle ( +- 1.22% ) (82.56%)
cache-references # 231.400 M/sec ( +- 0.56% ) (82.71%)
cache-misses # 8.797 % of all cache refs ( +- 15.29% ) (83.90%)
branches # 1011.101 M/sec ( +- 1.59% ) (83.90%)
branch-misses # 2.99% of all branches ( +- 0.49% ) (84.38%)
99.34 msec task-clock # 0.996 CPUs utilized ( +- 4.31% )
faults # 0.050 M/sec ( +- 0.07% )
minor-faults # 0.050 M/sec ( +- 0.07% )
cs # 0.007 K/sec ( +- 50.00% )
migrations # 0.000 K/sec
0.09976 +- 0.00448 seconds time elapsed ( +- 4.49% )
二、利用内建优化代码
写在一起的好处是：短代码往往意味着高性能，因为容易利用内建优化机制。
def laplacian(grid):
return np.roll(grid, +1) + np.roll(grid, -1) - 2 * grid
def evolve(grid, dt, D=1):
return grid + dt * D * laplacian(grid)
性能分析二：cache-references非常大，但0.97指令减少才是重点。
Performance counter stats for '/usr/local/anaconda3/bin/python3 diffusion_numpy.py' ( runs):
cycles # 3.368 GHz ( +- 2.05% ) (63.87%)
<not supported> stalled-cycles-frontend
<not supported> stalled-cycles-backend
instructions # 1.28 insn per cycle ( +- 0.41% ) (82.69%)
cache-references # 218.428 M/sec ( +- 0.44% ) (84.39%)
cache-misses # 10.430 % of all cache refs ( +- 4.03% ) (84.39%)
branches # 962.634 M/sec ( +- 1.17% ) (84.39%)
branch-misses # 2.99% of all branches ( +- 0.24% ) (82.97%)
102.48 msec task-clock # 0.998 CPUs utilized ( +- 2.02% )
faults # 0.049 M/sec ( +- 0.04% )
minor-faults # 0.049 M/sec ( +- 0.04% )
cs # 0.007 K/sec ( +- 50.00% )
migrations # 0.000 K/sec
0.10270 +- 0.00209 seconds time elapsed ( +- 2.04% )
三、降低内存分配、提高指令效率
找到 “正确的优化” 的点
我们使用 numpy降低了 CPU 负担，我们降低了解决问题所必要的内存分配次数。
事实上 evolve 函数有 93%的时间花费在 laplacian 函数中。
参见：[Optimized Python] 17 - Bottle-neck in performance
进一步优化
向操作系统进行请求所需的开销比简单填充缓存大很多。
填充一次缓存失效是一个在主板上优化过的硬件行为，而内存分配则需要跟另一个进程、内核打交道来完成。
（1）"+="运算符的使用减少了“不必要的变量内存分配”。
（2）roll_add替代过于全能的np.roll，以减少不必要的指令。
def roll_add(rollee, shift, out):
if shift == :
out[:] += rollee[:-]
out[] += rollee[-]
elif shift == -:
out[:-] += rollee[:]
out[-] += rollee[] def laplacian(grid, out):
np.copyto(out, grid)
np.multiply(out, -2.0, out)
roll_add(grid, +, out)
roll_add(grid, -, out) def evolve(grid, dt, out, D=1):
laplacian(grid, out)
np.multiply(out, D * dt, out)
np.add(out, grid, out
性能分析三：减低了内存缺页，提高了指令效率。
Performance counter stats for '/usr/local/anaconda3/bin/python3 diffusion_numpy_memory2.py' ( runs):
cycles # 3.670 GHz ( +- 1.89% ) (62.67%)
<not supported> stalled-cycles-frontend
<not supported> stalled-cycles-backend
instructions # 1.28 insn per cycle ( +- 0.19% ) (81.33%)
cache-references # 211.611 M/sec ( +- 2.65% ) (81.94%)
cache-misses # 12.672 % of all cache refs ( +- 6.84% ) (84.68%)
branches # 1034.575 M/sec ( +- 0.68% ) (86.00%)
branch-misses # 3.25% of all branches ( +- 1.19% ) (84.71%)
85.71 msec task-clock # 0.997 CPUs utilized ( +- 1.86% )
faults # 0.058 M/sec ( +- 0.10% )
minor-faults # 0.058 M/sec ( +- 0.10% )
cs # 0.004 K/sec ( +-100.00% )
migrations # 0.000 K/sec
0.08596 +- 0.00163 seconds time elapsed ( +- 1.89% )
四、整体处理表达式
numexpr 的一个重要特点是它考虑到了 CPU 缓存。它特地移动数据来让各级CPU 缓存能够拥有正确的数据让缓存失效最小化。
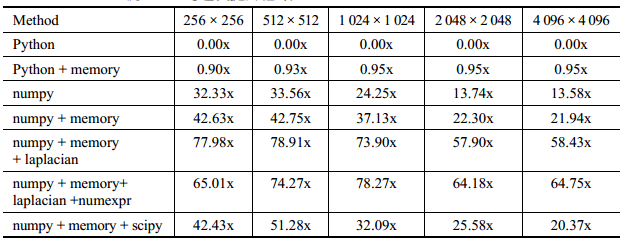
（a）当我们增加矩阵的大小时，我们会发现 numexpr 比原生 numpy 更好地利用了我们的缓存。而且，numexpr 利用了多核来进行计算并尝试填满每个核心的缓存。
（b）当矩阵较小时，管理多核的开销盖过了任何可能的性能提升。
import numexpr as ne def evolve(grid, dt, out, D=):
laplacian(grid, out)
ne.evaluate("out*D*dt+grid", out=out)
性能分析四：减低了内存缺页，提高了指令效率。
Performance counter stats for '/usr/local/anaconda3/bin/python3 diffusion_numpy_memory2_numexpr.py' ( runs):
cycles # 3.888 GHz ( +- 1.01% ) (65.40%)
<not supported> stalled-cycles-frontend
<not supported> stalled-cycles-backend
instructions # 1.23 insn per cycle ( +- 1.70% ) (82.72%)
cache-references # 232.372 M/sec ( +- 0.91% ) (82.89%)
cache-misses # 10.513 % of all cache refs ( +- 10.84% ) (83.77%)
branches # 1032.639 M/sec ( +- 1.21% ) (84.97%)
branch-misses # 3.21% of all branches ( +- 0.61% ) (82.97%)
100.18 msec task-clock # 1.000 CPUs utilized ( +- 5.75% )
faults # 0.086 M/sec ( +- 0.01% )
minor-faults # 0.086 M/sec ( +- 0.01% )
cs # 0.123 K/sec ( +- 2.70% )
migrations # 0.030 K/sec
0.10018 +- 0.00582 seconds time elapsed ( +- 5.81% )
五、利用现成的方案
直接使用scipy提供的接口。
from scipy.ndimage.filters import laplace def laplacian(grid, out):
laplace(grid, out, mode='wrap')
性能分析五：可能过于通用而没有明显提升。
Performance counter stats for '/usr/local/anaconda3/bin/python3 diffusion_scipy.py' ( runs):
cycles # 3.647 GHz ( +- 0.37% ) (63.49%)
<not supported> stalled-cycles-frontend
<not supported> stalled-cycles-backend
instructions # 1.28 insn per cycle ( +- 1.10% ) (81.74%)
cache-references # 223.757 M/sec ( +- 0.37% ) (82.77%)
cache-misses # 9.848 % of all cache refs ( +- 1.46% ) (84.55%)
96943942 branches # 1021.088 M/sec ( +- 0.80% ) (85.19%)
branch-misses # 3.22% of all branches ( +- 1.27% ) (84.00%)
94.94 msec task-clock # 0.997 CPUs utilized ( +- 11.09% )
faults # 0.054 M/sec ( +- 0.10% )
minor-faults # 0.054 M/sec ( +- 0.10% )
cs # 0.004 K/sec ( +-100.00% )
migrations # 0.000 K/sec
0.0952 +- 0.0106 seconds time elapsed ( +- 11.14% )
六、总结
看来，scipy没有大的必要，“定制的” 优化比较靠谱。
NumPy Data Structures
使用原生 List 作为 Array
In [1]:
v = [0.5, 0.75, 1.0, 1.5, 2.0] # vector of numbers
In [2]:
m = [v, v, v] # matrix of numbers
m
Out[2]:
[[0.5, 0.75, 1.0, 1.5, 2.0],
[0.5, 0.75, 1.0, 1.5, 2.0],
[0.5, 0.75, 1.0, 1.5, 2.0]]
In [3]:
m[1]
Out[3]:
[0.5, 0.75, 1.0, 1.5, 2.0]
In [4]:
m[1][0]
Out[4]:
0.5
In [5]:
v1 = [0.5, 1.5]
v2 = [1, 2]
m = [v1, v2]
c = [m, m] # cube of numbers
c
Out[5]:
[[[0.5, 1.5], [1, 2]], [[0.5, 1.5], [1, 2]]]
In [6]:
c[1][1][0]
Out[6]:
1
In [7]:
v = [0.5, 0.75, 1.0, 1.5, 2.0]
m = [v, v, v]
m
Out[7]:
[[0.5, 0.75, 1.0, 1.5, 2.0],
[0.5, 0.75, 1.0, 1.5, 2.0],
[0.5, 0.75, 1.0, 1.5, 2.0]]
In [8]:
v[0] = 'Python'
m
Out[8]:
[['Python', 0.75, 1.0, 1.5, 2.0],
['Python', 0.75, 1.0, 1.5, 2.0],
['Python', 0.75, 1.0, 1.5, 2.0]]
In [9]:
from copy import deepcopy
v = [0.5, 0.75, 1.0, 1.5, 2.0]
m = 3 * [deepcopy(v), ]
m
Out[9]:
[[0.5, 0.75, 1.0, 1.5, 2.0],
[0.5, 0.75, 1.0, 1.5, 2.0],
[0.5, 0.75, 1.0, 1.5, 2.0]]
In [10]:
v[0] = 'Python'
m
Out[10]:
[[0.5, 0.75, 1.0, 1.5, 2.0],
[0.5, 0.75, 1.0, 1.5, 2.0],
[0.5, 0.75, 1.0, 1.5, 2.0]]
使用 NumPy Arrays
In [11]:
import numpy as np
In [12]:
a = np.array([0, 0.5, 1.0, 1.5, 2.0])
type(a)
Out[12]:
numpy.ndarray
In [13]:
a[:2] # indexing as with list objects in 1 dimension
Out[13]:
array([ 0. , 0.5])
In [14]:
a.sum() # sum of all elements
Out[14]:
5.0
In [15]:
a.std() # standard deviation
Out[15]:
0.70710678118654757
In [16]:
a.cumsum() # running cumulative sum
Out[16]:
array([ 0. , 0.5, 1.5, 3. , 5. ])
In [17]:
a * 2
Out[17]:
array([ 0., 1., 2., 3., 4.])
In [18]:
a ** 2
Out[18]:
array([ 0. , 0.25, 1. , 2.25, 4. ])
In [19]:
np.sqrt(a)
Out[19]:
array([ 0. , 0.70710678, 1. , 1.22474487, 1.41421356])
In [20]:
b = np.array([a, a * 2])
b
Out[20]:
array([[ 0. , 0.5, 1. , 1.5, 2. ],
[ 0. , 1. , 2. , 3. , 4. ]])
In [21]:
b[0] # first row
Out[21]:
array([ 0. , 0.5, 1. , 1.5, 2. ])
In [22]:
b[0, 2] # third element of first row
Out[22]:
1.0
In [23]:
b.sum()
Out[23]:
15.0
In [24]:
b.sum(axis=0)
# sum along axis 0, i.e. column-wise sum
Out[24]:
array([ 0. , 1.5, 3. , 4.5, 6. ])
In [25]:
b.sum(axis=1)
# sum along axis 1, i.e. row-wise sum
Out[25]:
array([ 5., 10.])
In [26]:
c = np.zeros((2, 3, 4), dtype='i', order='C') # also: np.ones()
c
Out[26]:
array([[[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]], [[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]]], dtype=int32)
In [27]:
d = np.ones_like(c, dtype='f16', order='C') # also: np.zeros_like()
d
Out[27]:
array([[[ 1.0, 1.0, 1.0, 1.0],
[ 1.0, 1.0, 1.0, 1.0],
[ 1.0, 1.0, 1.0, 1.0]], [[ 1.0, 1.0, 1.0, 1.0],
[ 1.0, 1.0, 1.0, 1.0],
[ 1.0, 1.0, 1.0, 1.0]]], dtype=float128)
In [28]:
import random
I = 5000
In [29]:
%time mat = [[random.gauss(0, 1) for j in range(I)] for i in range(I)]
# a nested list comprehension
CPU times: user 21.3 s, sys: 238 ms, total: 21.5 s
Wall time: 21.5 s
In [30]:
%time mat = np.random.standard_normal((I, I))
CPU times: user 1.36 s, sys: 55.9 ms, total: 1.42 s
Wall time: 1.42 s
In [31]:
%time mat.sum()
CPU times: user 15.2 ms, sys: 0 ns, total: 15.2 ms
Wall time: 14.1 ms
Out[31]:
1137.43504265149
自定义 Arrays
In [32]:
dt = np.dtype([('Name', 'S10'), ('Age', 'i4'),
('Height', 'f'), ('Children/Pets', 'i4', 2)]) # 类似与数据库的表，定义列的属性；每列数据的类型是要确保一致的
s = np.array([('Smith', 45, 1.83, (0, 1)),
('Jones', 53, 1.72, (2, 2))], dtype=dt)
s
Out[32]:
array([(b'Smith', 45, 1.83000004, [0, 1]),
(b'Jones', 53, 1.72000003, [2, 2])],
dtype=[('Name', 'S10'), ('Age', '<i4'), ('Height', '<f4'), ('Children/Pets', '<i4', (2,))])
In [33]:
s['Name']
Out[33]:
array([b'Smith', b'Jones'],
dtype='|S10')
In [34]:
s['Height'].mean()
Out[34]:
1.7750001
In [35]:
s[1]['Age']
Out[35]:
53
Vectorization of Code
Basic Vectorization 向量化
In [36]:
r = np.random.standard_normal((4, 3))
s = np.random.standard_normal((4, 3))
In [37]:
r + s
Out[37]:
array([[ 1.33110811e+00, 1.26931718e+00, 4.43935711e-01],
[ -1.06905167e+00, 1.38422425e+00, -1.99126769e+00],
[ 3.24832612e-01, -6.63041986e-01, -1.11329038e+00],
[ 6.53171734e-01, -1.69497518e-05, 3.48108030e-01]])
In [38]:
2 * r + 3
Out[38]:
array([[ 6.23826763, 3.4056893 , 4.93537977],
[ 3.41201018, 3.18058875, 0.07823276],
[ 5.21407609, 2.93499984, 2.62703963],
[ 6.23041052, 6.13968592, 2.783421 ]])
In [39]:
s = np.random.standard_normal(3)
r + s
Out[39]:
array([[ 1.43696477, -0.89451367, -0.07713104],
[ 0.02383604, -1.00706394, -2.50570454],
[ 0.924869 , -1.12985839, -1.23130111],
[ 1.43303621, 0.47248465, -1.15311042]])
In [40]:
# causes intentional error
# s = np.random.standard_normal(4)
# r + s
In [41]:
# r.transpose() + s
In [42]:
np.shape(r.T)
Out[42]:
(3, 4)
In [43]:
def f(x):
return 3 * x + 5
In [44]:
f(0.5) # float object
Out[44]:
6.5
In [45]:
f(r) # NumPy array
Out[45]:
array([[ 9.85740144, 5.60853394, 7.90306966],
[ 5.61801527, 5.27088312, 0.61734914],
[ 8.32111413, 4.90249976, 4.44055944],
[ 9.84561578, 9.70952889, 4.6751315 ]])
In [46]:
# causes intentional error
# import math
# math.sin(r)
In [47]:
np.sin(r) # array as input
Out[47]:
array([[ 0.99883197, 0.20145647, 0.82357761],
[ 0.2045511 , 0.09017173, -0.99396568],
[ 0.89437769, -0.03249436, -0.18540126],
[ 0.99901409, 0.99999955, -0.10807798]])
In [48]:
np.sin(np.pi) # float as input
Out[48]:
1.2246467991473532e-16
结构组织方式
In [49]:
x = np.random.standard_normal((5, 10000000))
y = 2 * x + 3 # linear equation y = a * x + b
C = np.array((x, y), order='C') # 按行统计快些
F = np.array((x, y), order='F') # 按列统计快些
x = 0.0; y = 0.0 # memory clean-up
In [50]:
C[:2].round(2) # 四舍五入
Out[50]:
array([[[ 1.51, 0.67, -0.96, ..., -0.71, -1.55, 2.49],
[ 0.65, -0.15, 0.02, ..., 0.49, -0.26, 1.37],
[-0.07, 0.74, -2.31, ..., -0.51, 0.52, 0.49],
[ 0.52, -0.43, -0.18, ..., -0.06, 0.58, 1.46],
[-0.32, 0.59, -0.75, ..., -0.03, 0.23, -0.75]], [[ 6.01, 4.35, 1.07, ..., 1.58, -0.11, 7.97],
[ 4.3 , 2.71, 3.04, ..., 3.99, 2.48, 5.75],
[ 2.86, 4.48, -1.62, ..., 1.97, 4.04, 3.97],
[ 4.03, 2.14, 2.63, ..., 2.88, 4.16, 5.92],
[ 2.36, 4.19, 1.51, ..., 2.94, 3.46, 1.5 ]]])
In [51]:
%timeit C.sum()
10 loops, best of 3: 45.2 ms per loop
In [52]:
%timeit F.sum()
10 loops, best of 3: 48.2 ms per loop
In [53]:
%timeit C[0].sum(axis=0)
10 loops, best of 3: 66.4 ms per loop
In [54]:
%timeit C[0].sum(axis=1)
10 loops, best of 3: 22.8 ms per loop
In [55]:
%timeit F.sum(axis=0)
1 loop, best of 3: 712 ms per loop
In [56]:
%timeit F.sum(axis=1)
1 loop, best of 3: 1.64 s per loop
In [57]:
F = 0.0; C = 0.0 # memory clean-up
End.
[Pandas] 01 - A guy based on NumPy的更多相关文章
- 对pandas和pendulum的吐槽——TimeStamp numpy的datetime64的转型问题
今天被这俩货因为时间日期处理不兼容的问题折腾半天,气死人,不吐槽不行了! 这俩简称都可以是pd的库,都TM够轴的,互相兼容极差. pandas 和 pendulum 知名度都很高,也很常用.但我就是用 ...
- Pandas | 01 数据结构
Pandas的三种数据结构: 系列(Series) 数据帧(DataFrame) 面板(Panel) 这些数据结构,构建在Numpy数组之上,这意味着它们很快 维数和描述 考虑这些数据结构的最好方法是 ...
- pandas数据类型（二）与numpy的str和object类型之间的区别
现象: Numpy区分了str和object类型,其中dtype(‘S’)和dtype(‘O’)分别对应于str和object. 然而,pandas缺乏这种区别 str和object类型都对应dtyp ...
- [Pandas] 02 - Tutorial of NumPy
Ref: NumPy 教程 这里主要是查缺补漏一些常用方法. 初步认识 矩阵常见知识点 矩阵操作 Ref: [Python] 01 - Number and Matrix[总结过一部分] 一.矩阵 ( ...
- [Pandas] 05 - Parallel processing
相关资源 [Python] 09 - Multi-processing [Pandas] 01 - A guy based on NumPy [AI] 深度数学 - Bayes 这章非常有意思,但一定 ...
- [Optimized Python] 17 - Performance bottle-neck
前言 对于一门编程语言,没接触到“优化”和“库代码”的源码理解程度,不足以谈“掌握”二字. 本篇的学习笔记,同时也意味着自己终于触及到了Python的junior国际水准.(joke) 要学的东西有很 ...
- [Code] 大蛇之数据工程
作为“所谓码农”的首篇,本章内容理应涵盖基本编程技法. Python这个东西.简洁,作为载体,是个不错的选择呦. 链接资源: Python文档:https://docs.python.org/3/ 教 ...
- [AI] 深度数据 - Data
Data Engineering Data Pipeline Outline [DE] How to learn Big Data[了解大数据] [DE] Pipeline for Data Eng ...
- [Python] 09 - Multi-processing
前言 资源 Ref: Python3 多线程 Ref: Python3之多进程 # python中的多线程无法利用多核优势 更多的提高效率的策略,请参见:[Pandas] 01 - A g ...
随机推荐
- 以帧为存储单位的循环stack
此stack主要是作为存储空间使用,主要的借口就是push和pop. stack frame的src以及例程位于stack_FrameTest这个库当中,其中有readme文件,可以快速上手. sta ...
- SpringCould-------使用Hystrix 实现断路器进行服务容错保护
消费: <project xmlns="http://maven.apache.org/POM/4.0.0" xmlns:xsi="http://www.w3.or ...
- Kafka的消息会丢失和重复吗？——如何实现Kafka精确传递一次语义
我们都知道Kafka的吞吐量很大,但是Kafka究竟会不会丢失消息呢?又会不会重复消费消息呢? 图 无人机实时监控 有很多公司因为业务要求必须保证消息不丢失.不重复的到达,比如无人机实时监控系统, ...
- 《Java 8 in Action》Chapter 6：用流收集数据
1. 收集器简介 collect() 接收一个类型为 Collector 的参数,这个参数决定了如何把流中的元素聚合到其它数据结构中.Collectors 类包含了大量常用收集器的工厂方法,toLis ...
- CodeForces 1058E
题意略. 思路:本题有两个关键点: 一.满足题设的区间条件 1.区间内1的个数和为偶数 2.区间内含1个数最多的那一项,它所含1的个数不得超过区间内1的个数和的一半. 二.长度超过60的区间必然满足上 ...
- java虚拟机10.内存模型与线程
多任务处理在现代计算机操作系统中是一项必备的功能,让计算机同时去做几件事情,不仅是因为计算机的运算能力强大了,更重要的原因是计算机的运算速度与它的存储和通信子系统速度的差距太大,大量的时间都花费在磁盘 ...
- 问题.beego路由设置及请求参数传递
最近项目组安排将一组Lua实现的web服务端代码重构成Go实现,所以顺便学习了下Lua和Go,这里记录下在尝试重构的过程中遇到的几个问题. 1.beego路由设置 路由设置简单说下,主要是调用了pac ...
- Java 从入门到进阶之路（五）
之前的文章我们介绍了 Java 的循环结构,本章我们来看一下 Java 的数组 数组对于每一门编程语言来说都是重要的数据结构之一,当然不同语言对数组的实现及处理也不尽相同. 数组 - 相同数据类型的元 ...
- 计蒜客 ACM训练联盟周赛 第一场 Christina式方格取数 思维
助手Christina发明了一种方格取数的新玩法:在n*m的方格棋盘里,每个格子里写一个数.两个人轮流给格子染色,直到所有格子都染了色.在所有格子染色完后,计算双方的分数.对于任意两个相邻(即有公共边 ...
- SSH项目，JSP项目，SSM项目源码附带环境安装指导视频教程
基于java开发的一个局域网端口扫描程序下载地址:https://www.icodedock.com/article/6.html 用JAVA实现对JAVA代码的格式化下载地址:https://www ...