【枚举Day1】20170529-2枚举算法专题练习 题解

题目： http://www.cnblogs.com/ljc20020730/p/6918328.html

评测器：cena

评测记录：

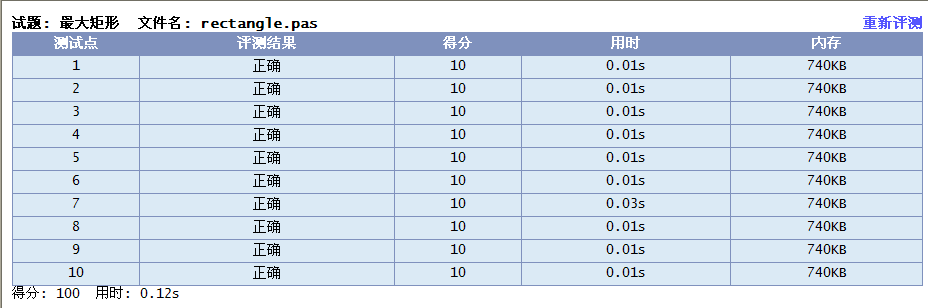
1.OneMoreRectangle 一个矩形

●如果任意枚举矩形坐标，显然不可行。数组太大，开不下！
●我们注意到，如果我们放入了矩形，矩形周围并没有其它矩形，那么稍微移动这个矩形，不会改变答案。
显然，一定存在一种方案，使得放入的矩形的边界与某些已知矩形边界重合。
我们不妨规定，放入的矩形下边界必须与已知矩形重合、左边界必须与已知矩形重合。

所以就可以做了

 type rec=record
 x1,y1,x2,y2:longint;
 end;
 var n,x,y,i,j,k,ans,max,xx,yy:longint;
     a:array[..]of rec;
 begin
 assign(input,'rectangle.in');
 assign(output,'rectangle.out');
 reset(input);
 rewrite(output);
  readln(n,x,y);
  for i:= to n do
  readln(a[i].x1,a[i].y1,a[i].x2,a[i].y2);
  for i:= to n do
   for j:= to n do begin
   xx:=a[i].x1; yy:=a[j].y1;
   ans:=;
   for k:= to n do
    if (a[k].x1>=xx)and(a[k].x1<=xx+x)and(a[k].y1>=yy)and(a[k].y2<=yy+y)
    and(a[k].x2>=xx)and(a[k].x2<=xx+x)and(a[k].y2>=yy)and(a[k].y2<=yy+y)
//这里是判断以第i个矩形的左下角坐横标X1,第j个矩形的左下角纵坐标Y1围成的X*Y的矩形能不能覆盖第k个矩形 
 then inc(ans); 
 if ans>max then max:=ans; 
 end; 
  writeln(max); 
  close(input); 
  close(output); 
 end.

评测记录：

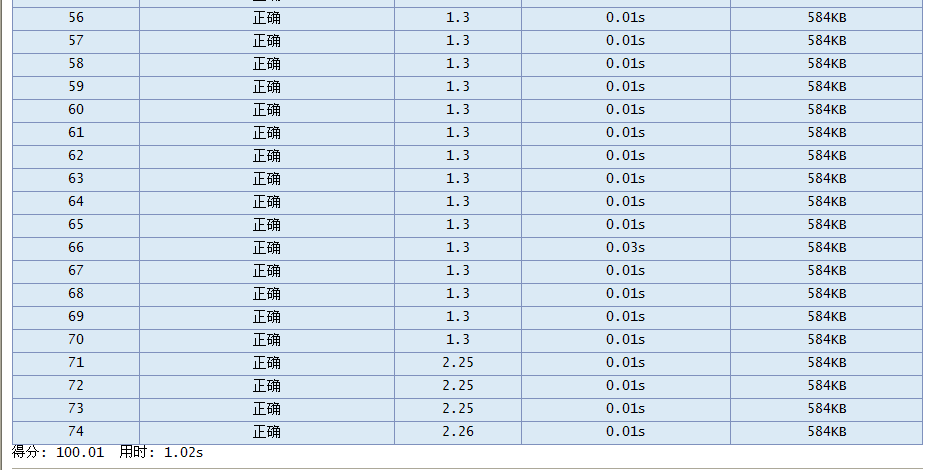
2.Palindromes回文

对于目前已经实现的算法的平均时间复杂度为O(length(s)*k/2)或许更少，

但是实在想不出办法来优化，于是就这样放在这里吧！

 var k,i,ans:longint;
     s:ansistring;
 function check(l,r:longint):boolean;//判断字符串s从l位到r位是否为回文
 var th:ansistring;
     i:longint;
 begin
  th:='';
  for i:=l to r do th:=th+s[i];
  for i:= to length(th)div + do
   if th[i]<>th[length(th)-i+] then exit(false);
  exit(true);
 end;
 begin
 assign(input,'palin.in');
 assign(output,'palin.out');
 reset(input);
 rewrite(output);
  readln(k);
  readln(s);
  for i:= to length(s) do begin
   if i+k->length(s) then break;
   if check(i,i+k-) then inc(ans);
  end;//枚举当前点和后面连这个点加起来为k位是否为回文

  writeln(ans); 
 close(input); 
 close(output); 
 end.

评测记录：

3.ProblemSetter(问题的设置)

一开始想的复杂，选排快排一起用太复杂了点。暴力好像拿了92分！

现在讲一种很简单的办法！

排序+枚举（排序：按照简单-中等-困难的顺序输出）
解决方法是：先从小到大枚举E，再从大到小枚举H，最后从小到大枚举M，取每个值第一个遇到的解。（注意枚举不重复）
“你希望难度差尽量接近”定义一个函数F(x,y,z:longint):longint;

function F(x,y,z:longint):longint;
begin
exit(abs((a[y]-[x])-(a[z]-a[y])));
end;

接下来是程序：

 var n,i,j,e,m,h,k:longint;
     a:array[..]of longint;
 procedure swap(var a,b:longint);
 var t:longint;
 begin
  t:=a; a:=b; b:=t;
 end;
 function f(x,y,z:longint):longint;
 begin
  exit(abs(abs(a[y]-a[x])-abs(a[z]-a[y])));
 end;
 begin
 assign(input,'problemsetter.in');
 assign(output,'problemsetter.out');
 reset(input);
 rewrite(output);
  readln(n);
  for i:= to n do read(a[i]);
  for i:= to n- do
   for j:=i+ to n do
    if a[i]>a[j] then swap(a[i],a[j]);
  E:=; M:=; H:=n;//这是所有组合中f最大的！
  for i:= to n do //任意
   for k:=n downto i+ do //从最后向前推，注意第i位是E的，第i+1位是M的，所以只能到i+2
    for j:=i+ to k- do //从E到H（不包含E和H）都可以选
      if f(i,j,k)<f(E,M,H) then begin
         E:=i;M:=j;H:=k;//迭代
      end;
  writeln(a[E],' ',a[M],' ',a[H]);//输出
  close(input);
  close(output);
 end.

评测记录：

4.ColoringRectangles着色的矩形

这道题需要遵循以下步骤

提供以下样例：

输入：

输出：

(1)递归求出每一个矩形被覆盖后能看到的面积（注意从后往前枚举，后保存当前编号ans[i]）。
定义一个过程：

procedure cal(l,r,b,t,z:longint); //z为从上到下的该层编号（看下还有多少可能的其他编号的矩形在上面）。
begin
while (z<=n) and ((r<=x1[z]) or (l>=x2[z]) or (t<=y1[z]) or (b>=y2[z])) do inc(z);//一些不符合条件的矩形
if z>n then begin inc(area[now],(r-l)*(t-b));exit;end; //求出area
if l<x1[z] then begin cal(l,x1[z],b,t,z+);l:=x1[z];end;
if r>x2[z] then begin cal(x2[z],r,b,t,z+);r:=x2[z];end;
if b<y1[z] then cal(l,r,b,y1[z],z+);
if t>y2[z] then cal(l,r,y2[z],t,z+);//分割成四块来求
end;

(2)按面积area从大到小，相同面积按编号从小到大编号排序

for i:= to n- do
  for j:=i+ to n do
  if (area[i]<area[j])or((area[i]=area[j])and(ans[i]>ans[j]))
  then begin swap(area[i],area[j]); swap(ans[i],ans[j]); end;

(3)再按编号从小到大对k个编号ans[]排序，这样可以按字典序输出。

 for i:= to k- do
  for j:=i+ to k do
   if ans[i]>ans[j] then swap(ans[i],ans[j]);

完整的程序：

 var x1,y1,x2,y2,area,ans:array[..]of longint;
     n,k,now,i,j:longint;
 procedure swap(var a,b:longint);
 var t:longint;
 begin
 t:=a; a:=b; b:=t;
 end;
 procedure cal(l,r,b,t,z:longint);
 begin
   while (z<=n) and ((r<=x1[z]) or (l>=x2[z]) or (t<=y1[z]) or (b>=y2[z])) do inc(z);
   if z>n then begin inc(area[now],(r-l)*(t-b));exit;end;
   if l<x1[z] then begin cal(l,x1[z],b,t,z+);l:=x1[z];end;
   if r>x2[z] then begin cal(x2[z],r,b,t,z+);r:=x2[z];end;
   if b<y1[z] then cal(l,r,b,y1[z],z+);
   if t>y2[z] then cal(l,r,y2[z],t,z+);
 end;
 begin
 assign(input,'rectangles.in');
 assign(output,'rectangles.out');
 reset(input);
 rewrite(output);
  readln(n,k);
  for i:= to n do read(x1[i]); readln;
  for i:= to n do read(y1[i]); readln;
  for i:= to n do read(x2[i]); readln;
  for i:= to n do read(y2[i]); readln;
  for i:=n downto  do begin
   ans[i]:=i;
   now:=i;
   cal(x1[now],x2[now],y1[now],y2[now],i+);
  end;
  for i:= to n- do
   for j:=i+ to n do
   if (area[i]<area[j])or((area[i]=area[j])and(ans[i]>ans[j]))
   then begin swap(area[i],area[j]); swap(ans[i],ans[j]); end;
  for i:= to k- do
   for j:=i+ to k do
    if ans[i]>ans[j] then swap(ans[i],ans[j]);
   for i:= to k- do write(ans[i]-,' ');
   writeln(ans[k]-);
   close(input);
   close(output);
 end.

 评测记录：