【HNOI2016】矿区

题面

题解

知识引入

1. 平面图

一个图\(G=(V,E)\)，若能将其画在平面上，且任意两条边的交点只能是\(G\)的顶点，则称\(G\)可嵌入平面，或称\(G\)是可平面的。

可平面图在平面上的一个嵌入称为一个平面图。如下图左边黑色的图为平面图，右边红色的图不属于平面图：

2. 平面图的对偶图

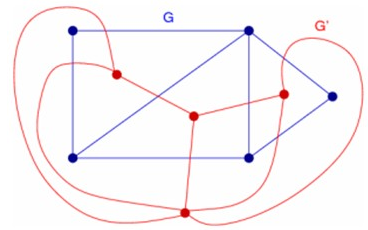
设有平面图\(G=(V,E)\)，满足下列条件的图\(G'= (V',E')\)称为图\(G\)的对偶图：

\(G\)的任一面\(R_i\)内有且仅有一点\(V_i'\)；对\(G\)的域\(R_i\)和\(R_j\)的共同边界\(E_k\)，画一条边\(E_k'=(V_i',V_j')\)且只与\(E_k\)交于一点；若\(E_k\)完全处于\(R_i\)中，则\(V_i'\)有一自环\(E_k'\)，如下图\(G'\)是\(G\)的对偶图：

本题题解

如何转对偶图，关键在于如何划分原图中的面，这个方法是先将双向边看成两条单向边，这样每一条边都属于一个面。

将每一条边按照极角排序，对于一条边\((s, t)\)，我们在以\(t\)为起点的边中找到\((t, s)\)，排序之后其上一条边就是当前面的下一条边界，这样一直找到整个区域闭合，就说明这个面上的边全部找出来了。这个步骤可以用vector存边。

建好了对偶图之后随意拿出一个生成树，以无边界的范围为根。

无边界的范围很好求，用叉积算出有向面积时，算出来是负数的就是无边界的范围。

然后标记所有的树边，记录生成树中每个子树的矿区面积和及面积平方和。

对于每一个询问，先找到询问里出现的边，如果有非树边就忽略，否则如果这条边所在的面是儿子，就加上子树的面积，如果是父亲就减去儿子子树的面积。

代码

#include<cstdio>
#include<cstring>
#include<cctype>
#include<cmath>
#include<algorithm>
#include<vector>
#define RG register
#define file(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout)
#define clear(x, y) memset(x, y, sizeof(x))

inline int read()
{
	int data = 0, w = 1; char ch = getchar();
	while(ch != '-' && (!isdigit(ch))) ch = getchar();
	if(ch == '-') w = -1, ch = getchar();
	while(isdigit(ch)) data = data * 10 + (ch ^ 48), ch = getchar();
	return data * w;
}

const int maxn(200010), maxm(1200010);
const double eps(1e-10);
int n, m, Q, cnt, root, e_num = 1, pos[maxm];
long long ans1, ans2;
struct point { int x, y; } p[maxn];
inline point operator - (const point &lhs, const point &rhs)
	{ return (point) {lhs.x - rhs.x, lhs.y - rhs.y}; }
inline long long operator * (const point &lhs, const point &rhs)
	{ return 1ll * lhs.x * rhs.y - 1ll * lhs.y * rhs.x; }
struct edge { int id, x, y; double ang; } e[maxm];
inline bool operator < (const edge &lhs, const edge &rhs)
{
	return fabs(lhs.ang - rhs.ang) < eps ?
		lhs.y < rhs.y : lhs.ang < rhs.ang;
}

long long sn[maxm], sd[maxm];
int next[maxm], fa[maxm], vis[maxm], ist[maxm], qry[maxm];
std::vector<edge> g[maxn], T[maxm];
inline void add_edge(int x, int y)
{
	++e_num; e[e_num] = (edge) {e_num, x, y,
		atan2(p[y].y - p[x].y, p[y].x - p[x].x)};
	g[x].push_back(e[e_num]);
}

void build()
{
	for(RG int i = 1; i <= n; i++) std::sort(g[i].begin(), g[i].end());
	for(RG int i = 2; i <= e_num; i++)
	{
		int y = e[i].y; std::vector<edge>::iterator _e =
			std::lower_bound(g[y].begin(), g[y].end(), e[i ^ 1]);
		if(_e == g[y].begin()) _e = g[y].end();
		--_e; next[i] = _e -> id;
	}
	for(RG int i = 2; i <= e_num; i++)
	{
		if(pos[i]) continue;
		pos[i] = pos[next[i]] = ++cnt;
		for(RG int j = next[i]; e[j].y != e[i].x; j = next[j], pos[j] = cnt)
			sd[cnt] += (p[e[j].x] - p[e[i].x]) * (p[e[j].y] - p[e[i].x]);
		if(sd[cnt] <= 0) root = cnt;
	}
	for(RG int i = 2; i <= e_num; i++)
		T[pos[i]].push_back((edge) {i, pos[i], pos[i ^ 1]});
}

void dfs(int x)
{
	sn[x] = 1ll * sd[x] * sd[x], sd[x] <<= 1, vis[x] = 1;
	for(RG int i = 0, sz = T[x].size(); i < sz; i++)
	{
		int y = T[x][i].y; if(vis[y]) continue;
		ist[T[x][i].id] = ist[T[x][i].id ^ 1] = 1;
		fa[y] = x; dfs(y); sd[x] += sd[y], sn[x] += sn[y];
	}
}

long long gcd(long long x, long long y)
{
	while(y) y ^= x ^= y ^= x %= y;
	return x;
}

int main()
{
	n = read(), m = read(), Q = read();
	for(RG int i = 1; i <= n; i++) p[i] = (point) {read(), read()};
	for(RG int i = 1, x, y; i <= m; i++) x = read(), y = read(),
		add_edge(x, y), add_edge(y, x);
	build(); dfs(root);
	while(Q--)
	{
		int num = (read() + ans1) % n + 1;
		for(RG int i = 1; i <= num; i++) qry[i] = (read() + ans1) % n + 1;
		qry[num + 1] = qry[1], ans1 = ans2 = 0;
		for(RG int i = 1; i <= num; i++)
		{
			int x = qry[i], y = qry[i + 1];
			edge e = (edge) {0, x, y, atan2(p[y].y - p[x].y, p[y].x - p[x].x)};
			std::vector<edge>::iterator _e =
				std::lower_bound(g[x].begin(), g[x].end(), e);
			int j = _e -> id; if(!ist[j]) continue;
			if(fa[pos[j]] == pos[j ^ 1]) ans1 += sn[pos[j]], ans2 += sd[pos[j]];
			else ans1 -= sn[pos[j ^ 1]], ans2 -= sd[pos[j ^ 1]];
		}
		long long tmp = gcd(ans1, ans2);
		ans1 /= tmp, ans2 /= tmp;
		printf("%lld %lld\n", ans1, ans2);
	}
	return 0;
}