2023-08-08：给你一棵 n 个节点的树（连通无向无环的图） 节点编号从 0 到 n - 1 且恰好有 n - 1 条边 给你一个长度为 n 下标从 0 开始的整数数组 vals 分别表示每个节

2023-08-08：给你一棵 n 个节点的树（连通无向无环的图）

节点编号从 0 到 n - 1 且恰好有 n - 1 条边

给你一个长度为 n 下标从 0 开始的整数数组 vals

分别表示每个节点的值

同时给你一个二维整数数组 edges

其中 edges[i] = [ai, bi] 表示节点 ai 和 bi 之间有一条 无向 边

一条 好路径 需要满足以下条件：

开始节点和结束节点的值 相同 。

开始节点和结束节点中间的所有节点值都 小于等于 开始节点的值。

（也就是说开始节点的值应该是路径上所有节点的最大值）。

请你返回不同好路径的数目。

注意，一条路径和它反向的路径算作 同一 路径。

比方说， 0 -> 1 与 1 -> 0 视为同一条路径。单个节点也视为一条合法路径。

输入：vals = [1,1,2,2,3], edges = [[0,1],[1,2],[2,3],[2,4]]。

输出：7。

来自谷歌。

来自左神

答案2023-08-08：

大致的步骤如下：

1.创建一个图（树）数据结构，并初始化节点的值和连接关系。

2.对节点的值进行排序，按照值的大小顺序处理节点。

3.初始化并查集，用于管理节点的连通性。

4.创建一个数组记录每个连通分量中值最大的节点的索引。

5.创建一个数组记录每个连通分量中值最大的节点所在连通分量的节点数。

6.初始化答案为节点的总数。

7.遍历排序后的节点列表，依次处理每个节点：

7.1.获取当前节点的索引和值。

7.2.查找当前节点的连通分量代表节点。

7.3.查找当前连通分量代表节点的最大值节点的索引。

7.4.遍历当前节点的邻居节点，将邻居节点的值与当前节点值进行比较。

7.5.若邻居节点的值小于等于当前节点值，并且邻居节点所在的连通分量与当前连通分量不同，则进行以下操作：

7.5.1.查找邻居节点连通分量的代表节点的最大值节点的索引。

7.5.2.若邻居节点的值等于该最大值节点的值，则更新答案并累加该最大值节点所在连通分量的节点数。

7.5.3.合并当前节点和邻居节点所在的连通分量。

7.5.4.更新当前连通分量代表节点的索引。

8.返回答案。

时间复杂度为O(nlogn)。

空间复杂度为O(n)。

go完整代码如下：

package main

import (
	"fmt"
	"sort"
)

func numberOfGoodPaths(vals []int, edges [][]int) int {
	n := len(vals)
	graph := make([][]int, n)
	for i := 0; i < n; i++ {
		graph[i] = make([]int, 0)
	}

	for _, e := range edges {
		graph[e[0]] = append(graph[e[0]], e[1])
		graph[e[1]] = append(graph[e[1]], e[0])
	}

	nodes := make([][]int, n)
	for i := 0; i < n; i++ {
		nodes[i] = make([]int, 2)
		nodes[i][0] = i
		nodes[i][1] = vals[i]
	}

	sort.Slice(nodes, func(i, j int) bool {
		return nodes[i][1] < nodes[j][1]
	})

	uf := NewUnionFind(n)
	maxIndex := make([]int, n)
	for i := 0; i < n; i++ {
		maxIndex[i] = i
	}

	maxCnts := make([]int, n)
	for i := 0; i < n; i++ {
		maxCnts[i] = 1
	}

	ans := n
	for _, node := range nodes {
		curi := node[0]
		curv := vals[curi]
		curCandidate := uf.Find(curi)
		curMaxIndex := maxIndex[curCandidate]
		for _, nexti := range graph[curi] {
			nextv := vals[nexti]
			nextCandidate := uf.Find(nexti)
			if curCandidate != nextCandidate && curv >= nextv {
				nextMaxIndex := maxIndex[nextCandidate]
				if curv == vals[nextMaxIndex] {
					ans += maxCnts[curMaxIndex] * maxCnts[nextMaxIndex]
					maxCnts[curMaxIndex] += maxCnts[nextMaxIndex]
				}
				candidate := uf.Union(curi, nexti)
				maxIndex[candidate] = curMaxIndex
			}
		}
	}

	return ans
}

type UnionFind struct {
	parent []int
	size   []int
	help   []int
}

func NewUnionFind(n int) *UnionFind {
	uf := &UnionFind{
		parent: make([]int, n),
		size:   make([]int, n),
		help:   make([]int, n),
	}
	for i := 0; i < n; i++ {
		uf.parent[i] = i
		uf.size[i] = 1
	}
	return uf
}

func (uf *UnionFind) Find(i int) int {
	hi := 0
	for i != uf.parent[i] {
		uf.help[hi] = i
		hi++
		i = uf.parent[i]
	}
	for hi--; hi >= 0; hi-- {
		uf.parent[uf.help[hi]] = i
	}
	return i
}

func (uf *UnionFind) Union(i, j int) int {
	f1 := uf.Find(i)
	f2 := uf.Find(j)
	if f1 != f2 {
		if uf.size[f1] >= uf.size[f2] {
			uf.size[f1] += uf.size[f2]
			uf.parent[f2] = f1
			return f1
		} else {
			uf.size[f2] += uf.size[f1]
			uf.parent[f1] = f2
			return f2
		}
	}
	return f1
}

func main() {
	vals := []int{1, 1, 2, 2, 3}
	edges := [][]int{{0, 1}, {1, 2}, {2, 3}, {2, 4}}
	result := numberOfGoodPaths(vals, edges)
	fmt.Println(result)
}

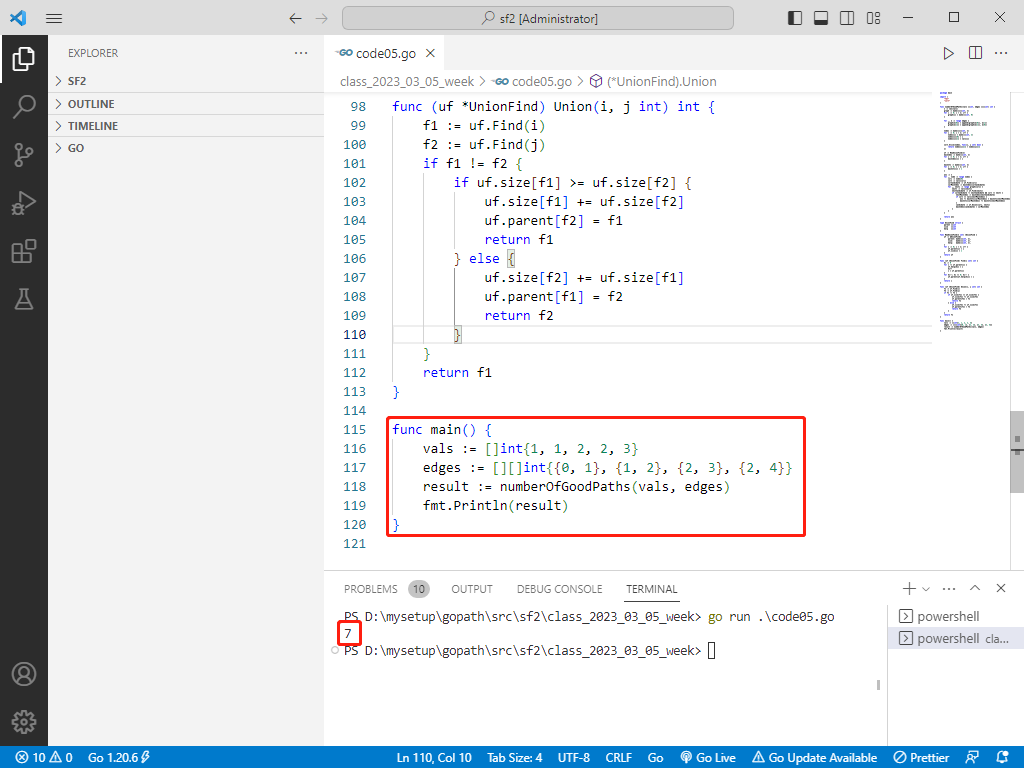
rust完整代码如下：

use std::cmp::Ordering;

fn number_of_good_paths(vals: Vec<i32>, edges: Vec<Vec<i32>>) -> i32 {
    let n = vals.len();
    let mut graph: Vec<Vec<i32>> = vec![Vec::new(); n];

    for edge in edges {
        let a = edge[0] as i32;
        let b = edge[1] as i32;
        graph[a as usize].push(b);
        graph[b as usize].push(a);
    }

    let mut nodes: Vec<[i32; 2]> = vals
        .iter()
        .enumerate()
        .map(|(i, &v)| [i as i32, v as i32])
        .collect();
    nodes.sort_by(|a, b| a[1].cmp(&b[1]));

    let mut uf = UnionFind::new(n as i32);
    let mut max_index: Vec<i32> = (0..n as i32).collect();
    let mut max_counts: Vec<i32> = vec![1; n];
    let mut ans = n as i32;

    for node in nodes {
        let cur_i = node[0];
        let cur_v = vals[cur_i as usize];
        let cur_candidate = uf.find(cur_i);
        let cur_max_index = max_index[cur_candidate as usize];

        for &next_i in &graph[cur_i as usize] {
            let next_v = vals[next_i as usize];
            let next_candidate = uf.find(next_i);

            if cur_candidate != next_candidate && cur_v >= next_v {
                let next_max_index = max_index[next_candidate as usize];

                if cur_v == vals[next_max_index as usize] {
                    ans += max_counts[cur_max_index as usize] * max_counts[next_max_index as usize];
                    max_counts[cur_max_index as usize] += max_counts[next_max_index as usize];
                }

                let candidate = uf.union(cur_i, next_i);
                max_index[candidate as usize] = cur_max_index;
            }
        }
    }

    ans
}

struct UnionFind {
    parent: Vec<i32>,
    size: Vec<i32>,
    help: Vec<i32>,
}

impl UnionFind {
    fn new(n: i32) -> UnionFind {
        UnionFind {
            parent: (0..n).collect(),
            size: vec![1; n as usize],
            help: Vec::new(),
        }
    }

    fn find(&mut self, i: i32) -> i32 {
        let mut hi = 0;
        let mut x = i;

        while x != self.parent[x as usize] {
            self.help.push(x);
            x = self.parent[x as usize];
            hi += 1;
        }

        for hi in (0..hi).rev() {
            self.parent[self.help[hi as usize] as usize] = x;
        }

        self.help.clear();

        x
    }

    fn union(&mut self, i: i32, j: i32) -> i32 {
        let f1 = self.find(i);
        let f2 = self.find(j);

        if f1 != f2 {
            if self.size[f1 as usize] >= self.size[f2 as usize] {
                self.size[f1 as usize] += self.size[f2 as usize];
                self.parent[f2 as usize] = f1;
                return f1;
            } else {
                self.size[f2 as usize] += self.size[f1 as usize];
                self.parent[f1 as usize] = f2;
                return f2;
            }
        }

        f1
    }
}

fn main() {
    let vals = vec![1, 1, 2, 2, 3];
    let edges = vec![vec![0, 1], vec![1, 2], vec![2, 3], vec![2, 4]];

    let result = number_of_good_paths(vals, edges);
    println!("Number of good paths: {}", result);
}

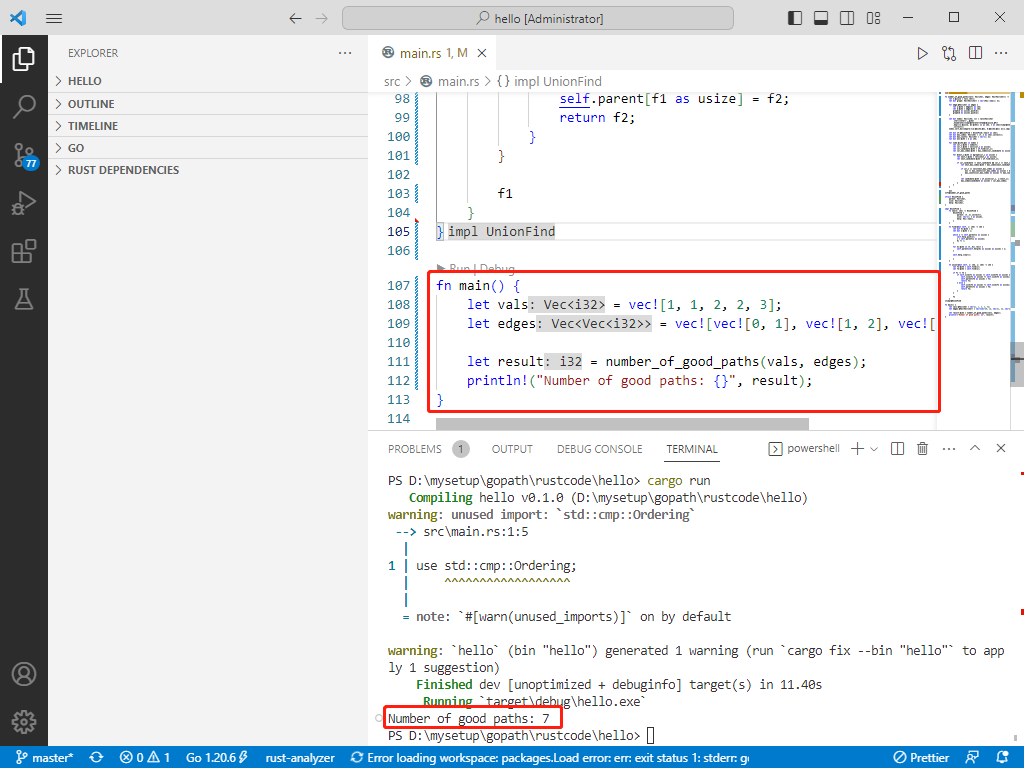
c++完整代码如下：

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

int numberOfGoodPaths(vector<int>& vals, vector<vector<int>>& edges) {
    int n = vals.size();

    // Build the graph
    vector<vector<int>> graph(n);
    for (auto& edge : edges) {
        int a = edge[0];
        int b = edge[1];
        graph[a].push_back(b);
        graph[b].push_back(a);
    }

    // Sort the nodes based on values
    vector<pair<int, int>> nodes;
    for (int i = 0; i < n; i++) {
        nodes.push_back({ vals[i], i });
    }
    sort(nodes.begin(), nodes.end());

    vector<int> parent(n);
    vector<int> size(n, 1);
    vector<int> maxIndex(n);
    vector<int> maxCnts(n, 1);

    for (int i = 0; i < n; i++) {
        parent[i] = i;
        maxIndex[i] = i;
    }

    int ans = n;

    // Traverse the nodes in ascending order of values
    for (int i = 0; i < n; i++) {
        int curi = nodes[i].second;
        int curv = vals[curi];
        int curCandidate = parent[curi];
        int curMaxIndex = maxIndex[curCandidate];

        // Iterate over the neighbors
        for (int nexti : graph[curi]) {
            int nextv = vals[nexti];
            int nextCandidate = parent[nexti];

            if (curCandidate != nextCandidate && curv >= nextv) {
                int nextMaxIndex = maxIndex[nextCandidate];

                if (curv == vals[nextMaxIndex]) {
                    ans += maxCnts[curMaxIndex] * maxCnts[nextMaxIndex];
                    maxCnts[curMaxIndex] += maxCnts[nextMaxIndex];
                }

                int candidate = parent[curi] = parent[nexti] = curMaxIndex;
                maxIndex[candidate] = curMaxIndex;
            }
        }
    }

    return ans;
}

int main() {
    vector<int> vals = { 1, 1, 2, 2, 3 };
    vector<vector<int>> edges = { {0, 1}, {1, 2}, {2, 3}, {2, 4} };

    int result = numberOfGoodPaths(vals, edges);
    cout << "Number of Good Paths: " << result << endl;

    return 0;
}

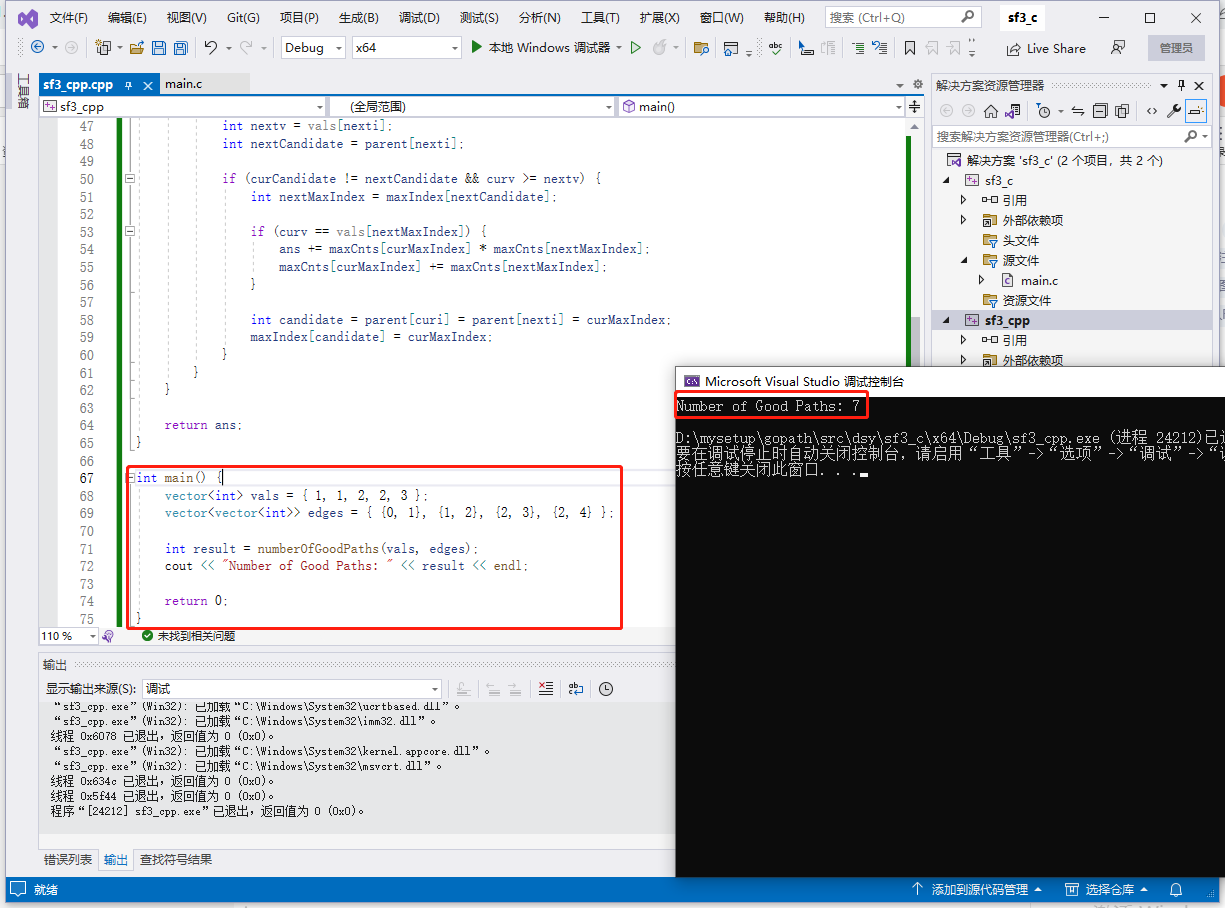
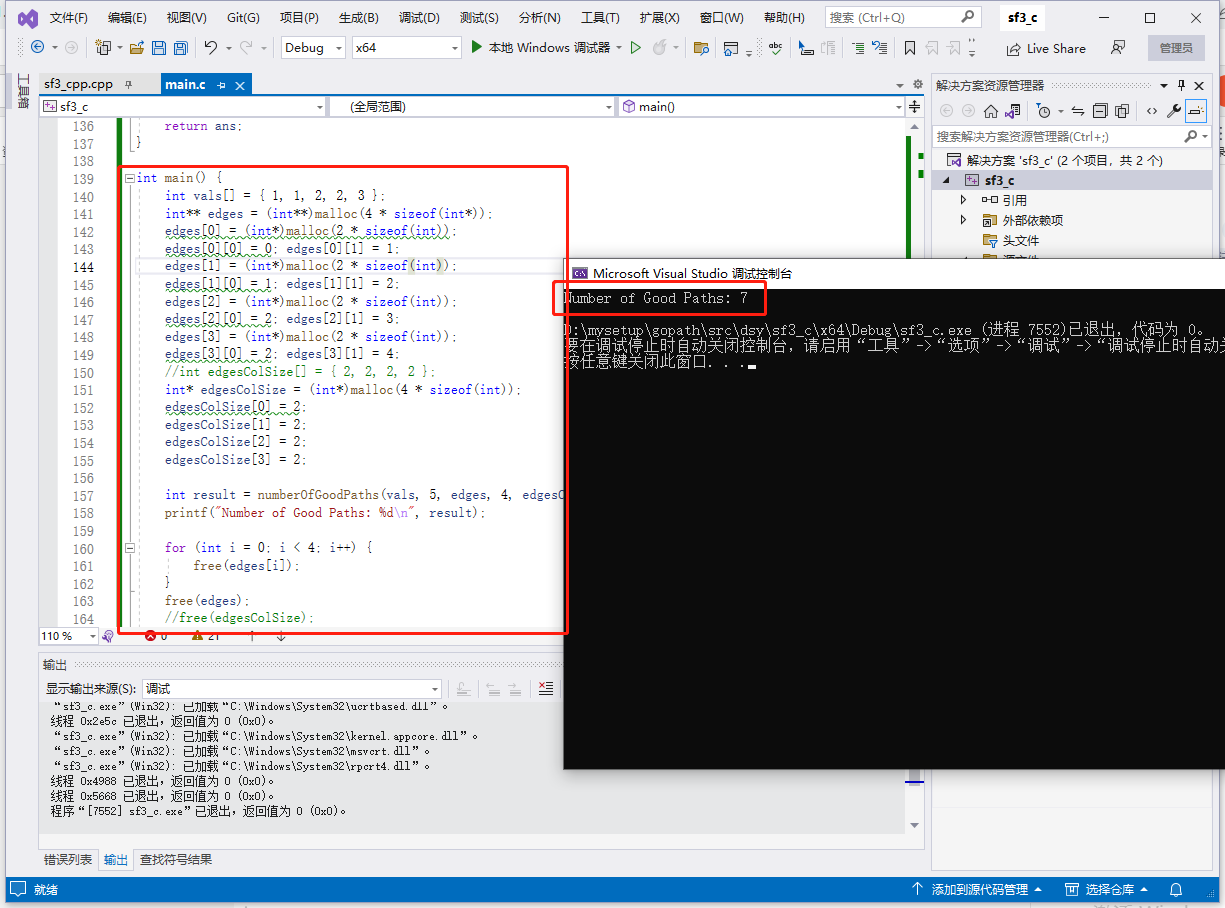
c完整代码如下：

#include <stdio.h>
#include <stdlib.h>

struct UnionFind {
    int* parent;
    int* size;
    int* help;
};

struct UnionFind* createUnionFind(int n) {
    struct UnionFind* uf = (struct UnionFind*)malloc(sizeof(struct UnionFind));
    uf->parent = (int*)malloc(n * sizeof(int));
    uf->size = (int*)malloc(n * sizeof(int));
    uf->help = (int*)malloc(n * sizeof(int));
    int i;
    for (i = 0; i < n; i++) {
        uf->parent[i] = i;
        uf->size[i] = 1;
    }
    return uf;
}

int find(struct UnionFind* uf, int i) {
    int hi = 0;
    while (i != uf->parent[i]) {
        uf->help[hi++] = i;
        i = uf->parent[i];
    }
    for (hi--; hi >= 0; hi--) {
        uf->parent[uf->help[hi]] = i;
    }
    return i;
}

int unionSet(struct UnionFind* uf, int i, int j) {
    int f1 = find(uf, i);
    int f2 = find(uf, j);
    if (f1 != f2) {
        if (uf->size[f1] >= uf->size[f2]) {
            uf->size[f1] += uf->size[f2];
            uf->parent[f2] = f1;
            return f1;
        }
        else {
            uf->size[f2] += uf->size[f1];
            uf->parent[f1] = f2;
            return f2;
        }
    }
    return f1;
}

// Comparison function for qsort
int compare(const void* a, const void* b) {
    int* na = *(int**)a;
    int* nb = *(int**)b;
    return na[1] - nb[1];
}

int numberOfGoodPaths(int* vals, int valsSize, int** edges, int edgesSize, int* edgesColSize) {
    int n = valsSize;
    int i, j;

    // 创建图
    int** graph = (int**)malloc(n * sizeof(int*));
    for (i = 0; i < n; i++) {
        graph[i] = (int*)malloc(n * sizeof(int));
        edgesColSize[i] = 0;
    }
    for (i = 0; i < edgesSize; i++) {
        int u = edges[i][0];
        int v = edges[i][1];
        graph[u][edgesColSize[u]++] = v;
        graph[v][edgesColSize[v]++] = u;
    }

    // 创建节点数组
    int** nodes = (int**)malloc(n * sizeof(int*));
    for (i = 0; i < n; i++) {
        nodes[i] = (int*)malloc(2 * sizeof(int));
        nodes[i][0] = i;
        nodes[i][1] = vals[i];
    }

    // 根据节点值排序
    qsort(nodes, n, sizeof(nodes[0]),compare);

    // 创建并初始化并查集
    struct UnionFind* uf = createUnionFind(n);
    int* maxIndex = (int*)malloc(n * sizeof(int));
    int* maxCnts = (int*)malloc(n * sizeof(int));
    for (i = 0; i < n; i++) {
        maxIndex[i] = i;
        maxCnts[i] = 1;
    }
    int ans = n;

    // 遍历节点
    for (i = 0; i < n; i++) {
        int curi = nodes[i][0];
        int curv = vals[curi];
        int curCandidate = find(uf, curi);
        int curMaxIndex = maxIndex[curCandidate];

        // 遍历邻居
        for (j = 0; j < edgesColSize[curi]; j++) {
            int nexti = graph[curi][j];
            int nextv = vals[nexti];
            int nextCandidate = find(uf, nexti);
            if (curCandidate != nextCandidate && curv >= nextv) {
                int nextMaxIndex = maxIndex[nextCandidate];
                if (curv == vals[nextMaxIndex]) {
                    ans += maxCnts[curMaxIndex] * maxCnts[nextMaxIndex];
                    maxCnts[curMaxIndex] += maxCnts[nextMaxIndex];
                }
                int candidate = unionSet(uf, curi, nexti);
                maxIndex[candidate] = curMaxIndex;
            }
        }
    }

    // 释放内存
    for (i = 0; i < n; i++) {
        free(graph[i]);
        free(nodes[i]);
    }
    free(graph);
    free(nodes);
    free(maxIndex);
    free(maxCnts);
    free(uf->parent);
    free(uf->size);
    free(uf->help);
    free(uf);

    return ans;
}

int main() {
    int vals[] = { 1, 1, 2, 2, 3 };
    int** edges = (int**)malloc(4 * sizeof(int*));
    edges[0] = (int*)malloc(2 * sizeof(int));
    edges[0][0] = 0; edges[0][1] = 1;
    edges[1] = (int*)malloc(2 * sizeof(int));
    edges[1][0] = 1; edges[1][1] = 2;
    edges[2] = (int*)malloc(2 * sizeof(int));
    edges[2][0] = 2; edges[2][1] = 3;
    edges[3] = (int*)malloc(2 * sizeof(int));
    edges[3][0] = 2; edges[3][1] = 4;
    //int edgesColSize[] = { 2, 2, 2, 2 };
    int* edgesColSize = (int*)malloc(4 * sizeof(int));
    edgesColSize[0] = 2;
    edgesColSize[1] = 2;
    edgesColSize[2] = 2;
    edgesColSize[3] = 2;

    int result = numberOfGoodPaths(vals, 5, edges, 4, edgesColSize);
    printf("Number of Good Paths: %d\n", result);

    for (int i = 0; i < 4; i++) {
        free(edges[i]);
    }
    free(edges);
    //free(edgesColSize);

    return 0;
}