11-02 NOIP练习赛

为什么休息的天还要打练习赛，这不公平！！！！！！！！！！ oh no！

但是三道题确实挺简单，也少见的很有意思。

[USACO23OPEN] Milk Sum S

题面翻译

给定数组 $a_1,...,a_N$ 在数组中依次选出一个元素构成排列 $b_1,...,b_N$ 。定义 $T = \sum _{i=1} ^N i \times b_i $ 。现在给出 $Q$ 个操作，每个操作有两个数 $x$ 和 $y$ 表示将 $a_x$ 替换成 $y$ ，对于每一个操作求出操作后的 $T$ 的最大值，每次操作后数组还原成原样。

输入格式

The first line contains $N$.

The second line contains $a_1\dots a_N$.

The third line contains $Q$.

The next $Q$ lines each contain two space-separated integers $i$ and $j$.

输出格式

Please print the value of $T$ for each of the $Q$ queries on separate lines.

样例输入 #1

样例输出 #1

$1\le N\le 1.5\cdot 10^5$, $0 \leq a_i \leq 10^8$,$1\le Q\le 1.5\cdot 10^5$，$0 \leq j \leq 10^8$.

第一题确实就比较简单，很明显排个序，更大的 $a_i$ 理应适配给大的 $i$ 以此来获得最大的 $T$。

替换操作又是没有后继性的，所以直接开搞。

朴素思想，将 $a_i$ 改动以后，其实就是将其放到它该在的地方，在排好的序列中二分找到正确的地方，并把受影响的元素依次移动一个。

考虑对答案的贡献，首先预处理出原始的 $T$，修改操作即先将 $a_i$ 的贡献删掉，然后将改动后的新贡献加入，再考虑受影响的部分，预处理一个前缀和，受影响部分的贡献其实就是这段区间的综合。时间复杂度 $O(nlogn)$。

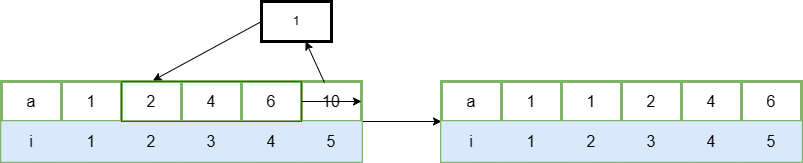
第一个样例解释

AC 代码：

#include<bits/stdc++.h>

using namespace std;

#define N 500005

#define int long long

long long a[N],f[N],pre[N],T=0;

long long n,q;

//我没有下一个运动会可以拿来错过了。

signed main(){

	freopen("a.in","r",stdin);

	freopen("a.out","w",stdout);

	scanf("%lld",&n);

	for(int i=1;i<=n;i++){

		scanf("%lld",&a[i]);

		f[i]=a[i];

	}

	sort(f+1,f+1+n);

	for(int i=1;i<=n;i++){

		T+=f[i]*i;pre[i]=f[i]+pre[i-1];

	}

	scanf("%lld",&q);

	while(q--){

		long long x,y;

		scanf("%lld%lld",&x,&y);

		int i=upper_bound(f+1,f+n+1,a[x])-f-1;

		int j=upper_bound(f+1,f+n+1,y)-f;

//		printf("%d %d\n",i,j);

		long long ans=T;

		if(i>=j) ans=T-i*a[x]+j*y+pre[i-1]-pre[j-1];

		else ans=T-i*a[x]+(j-1)*y+pre[i]-pre[j-1];

		printf("%lld\n",ans);

	}

	return 0;

}

十年 OI 一场空，不开 long long 见祖宗

是的，赛时没开 long long 直接挂 18 分。

[USACO23OPEN] Field Day S

题目描述

Farmer John 的 $N$ 个牛棚都会选出包含 $C$ 只奶牛的队伍去参加户外聚会。所有奶牛的品种都只可能是根西牛（G）或荷斯坦奶牛（H）。

我们将两个奶牛队伍中，同一位置对应的两头奶牛品种不同的所有位置 $i(1 \leq i \leq C)$ 的个数，定义为的两个奶牛队伍的差异。对于编号 $1...N$ 的每个奶牛队伍 $t$，请计算出 $t$ 和其它所有队伍的差异的最大值。

输入格式

第一行包含两个整数 $C$ 与 $N$。

接下来 $N$ 行，每行有一个长度为 $C$ 的，仅包含字母 G 和 H 的字符串，每行对应一支奶牛队伍。

输出格式

对于每个队伍，输出差异最大值。

$2 \leq N \leq 10^5,1 \leq C \leq 18$。

样例输入 #1

5 3

GHGGH

GHHHH

HGHHG

样例输出 #1

无法理解这道题 $O(n^2)$ 只给我 5 分什么意思，感觉这道题太简单了吗？

这道题也是我感觉 3 道题之中最有意思的一道题。

本题可以使用广度优先搜索。

将 G 和 H 视为二进制下的 0 和 1，本题就可以转化成：

$∀1≤i≤n$，求 $\max popcount(a_i⨁a_j)$ 的值。

考虑广搜，对于每个给出的整数为源点开始搜。每次搜与它只差一位的数，若该数没被搜过，该数距离 +1，将该整数放入队列。

这样跑完以后，每个数对应的距离就是他们和他们相差位数最少的数差几位。注意是所有的数全部跑一边，处理出离他们最近的原点。

那么，我想要找到与 $a_i$ 每位差的最远的数，就把 $a_i$ 取反以后找和它每位差的最少的数，也就是我们刚刚跑出来的距离。

AC 代码：

#include<bits/stdc++.h>

using namespace std;

int main(){

freopen("b.in","r",stdin);

	freopen("b.out","w",stdout);

  ios::sync_with_stdio(false);

  int c,n; cin>>c>>n;

  vector<int> a(n),m(1<<c,-1);

  queue<pair<int,int> > q;

  for(auto &i:a){

    for(int j=0;j<c;j++){

      char x; cin>>x;

      if(x=='G')i|=1<<j;

    }

    q.emplace(i,m[i]=0);

  }

  while(!q.empty()){

    auto [u,w]=q.front(); q.pop();

    for(int i=0;i<c;i++)

      if(int v=u^(1<<i);m[v]==-1)

        q.emplace(v,m[v]=w+1);

  }

  for(int i:a)cout<<c-m[(1<<c)-1^i]<<endl;

  return 0;

}

[USACO23OPEN] Pareidolia S

题面翻译

Farmer John有的时候看东西会忽略一些字母，如把 bqessiyexbesszieb 看成 bessiebessie。定义 $B(s)$ 表示把 $s$ 中的若干个字母删去后，形成尽量多个 bessie 相连的形式 (bessiebessiebessieb...)，返回 bessie 的最大数量。如 $B(\text{"bqessiyexbesszieb"})=2$。对字符串 $s$ 计算 $B(s)$ 是一个有趣的挑战，但FJ想到了一个更有趣的挑战：对 $s$ 的所有子串进行计算B函数，并求和。$s$ 的长度不超过 $3\times 10^5$。

样例输入 #1

bessiebessie

样例输出 #1

第三题题意还是比较简单，但是要 $O(n)$ 做出来还是需要一些技巧。

这道题的关键是抓住每一个 bessie 对答案的贡献，而不能抓子串。

考虑类似动态规划的思路，对于每一个 $i$，我们令 $f_i$ 表示以 $i$ 作为结尾的区间中总共有多少 bessie 。然后从头到尾统计答案，对于每个 $i$ 我们统计以 $a_i$ 结尾的所有子串能有多少贡献，看代码，还是比较好理解，不行就拿样例理解理解。

AC 代码：

#include<bits/stdc++.h>

#define LL long long

using namespace std;

const LL N=5e5;

char c[N];

LL n,lst[N],f[N],ans;

int main(){

	freopen("c.in","r",stdin);

	freopen("c.out","w",stdout);

	scanf("%s",c+1);

	n=strlen(c+1);

	for(int i=1;i<=n;i++){

		if(c[i]=='b')lst[1]=i;

		if(c[i]=='e')lst[2]=lst[1],lst[6]=lst[5];

		if(c[i]=='s')lst[4]=lst[3],lst[3]=lst[2];

		if(c[i]=='i')lst[5]=lst[4];

		f[i]=f[lst[6]-1]+lst[6];

		ans+=f[i];

	}

	printf("%lld",ans);

	return 0;

}