近五年的APIO

[APIO2018] 铁人两项

题意：给定一个张图，询问其中有多少个有序三元组 $(u,v,w)$，满足存在一条从 $u$ 到 $w$ 的简单路径，经过点 $v$。

考虑建出原图的圆方树。可以在圆方树上进行树形DP，分别对于圆点和方点的情况讨论即可。

复杂度可以做到 $O(n+m)$。

题意：图中有 $n$ 个圆，按照半径从大到小的顺序删除圆，同时删去与其相交或相切的所有圆，问每一个圆是被哪一个圆删掉的。

感觉这个东西并不好数据结构维护，所以考虑暴力。

首先记当前最大的圆为 $R$，如果我们将整个网格分割成边长为 $2R$ 的正方形，则只需要枚举与它所在格子及其它八连通的九个格子即可。

这样的构造使用哈希可以做到单次 $O(n)$。

但是这样的方格在做到足够大的时候是不优的，所以我们要考虑当前最长的半径 $R_0<\dfrac{R}{2}$ 时，进行一次重构，我们会重构 $O(\log W)$ 次，在每一层，它最多都会被暴力查找 $O(1)$ 次（具体来说最多36次），所以整体复杂度会是 $O(n\log W)$ 的。

[APIO2018] 新家

题意：有 $n$ 家商店，每一个商店属于一个种类，且在某一段时间内在某一个位置出现。$Q$ 次询问，求对于每一个时间点的某一位置，找到最小的 $l$，使得到每一种商店的最短距离均小于 $l$，或判断无解。

使用二分答案，题目转化为判断一个区间内是否有所有 $k$ 种商店，同时支持插入和删除。

对于每一个商店，维护他前一个的与它种类相同的店的位置，如果 $[r,+\infty)$ 的所有点中这个值的最小值 $\geqslant l$，说明在 $[l,r]$ 中出现了所有 $k$ 种商店，在 $\pm\infty$ 处插入每一种商店各一个即可。时间复杂度 $O(n\log^2n)$。

[APIO2019] 桥梁

题意：给定一张图，边有边权，支持两种操作：修改一条边的边权，查询从某个点开始只经过边权 $\geqslant v$ 的边能到达多少节点。

对操作序列进行分块，每次读入 $B$ 个操作，将所有的询问从大到小排序，同时将所有的在 $B$ 次操作中没有修改的边从大到小依次加入，使用并查集维护连通块。求解询问的答案是，将所有修改过权值的边扫一遍加入即可。需要使用可撤销并查集。

计算时间复杂度，单次处理，复杂度为 $O(m\log m+m\log n+B^2\log n)$，需要处理 $\dfrac{q}{B}$ 次，时间复杂度为 $O(\dfrac{q}{B}(m\log m+m\log n+B^2\log n))$，找到合适的 $B$ 均摊复杂度即可。

[APIO2019] 奇怪装置

题意：对于整数 $t$，生成有序数对 $(x,y)$，其中 $x=(t+\left\lfloor\dfrac{t}{B}\right\rfloor)\bmod A,y=t\bmod B$，询问对于所有整数 $t\in \bigcup\limits_{i=1}^n[l_i,r_i]$，一共能生成多少个本质不同的数对。

由于 $y\in[0,B)$ 将数对 $(x,y)$ 转化为数 $x\times B+y$，将 $x,y$ 代入，即为 $t(B+1)\bmod AB$，考虑最小的正整数 $t_0$，使得 $t_0(B+1)\equiv 0\pmod{AB}$。

由于 $B$ 与 $B+1$ 互质，则 $t_0=\dfrac{AB}{\gcd(A,B+1)}$。

原题转化为询问原来的所有区间，有多少本质不同的 $t\bmod t_0$，是从离散化和差分即可，时间复杂度 $O(n\log n)$

[APIO2019] 路灯

题意：有一个长为 $n$ 的 $01$ 序列，支持两种操作：翻转单点 $01$ 状态，查询到目前一共有多少个时刻满足 $[l,r]$ 的所有数均为 $1$。

维护原序列中的极长 $1$ 串，显然为原序列中的若干个不交区间，而每一次修改只会改变至多 $2$ 个区间，可以使用set维护（其实就和ODT很像）。

则 set 中每一个 $[l,r]$ 代表所有 $l\leqslant l_0<r_0\leqslant r$ 均满足条件，考虑对其进行差分，在消失时加上 $t$ 的贡献，在出现时减去 $-t$ 的贡献。

使用线段树套动态开点线段树实现矩阵加，单点查，时间复杂度 $O(m\log^2n)$。

[APIO2020] 粉刷墙壁

题意：现在有一面分为若干块墙壁，每一块需要被刷成特定的颜色，现在有若干家公司，每一家公司刷特定的几个颜色，每一次操作选择和公司数等量的墙壁，按照从某家公司开始顺序各刷一面墙，每一个公司只会刷这个公司特定的颜色。问至少进行多少次操作才能把墙刷完。

如果我们知道了从每一个位置开始能否将连续的 $M$ 面墙刷完，就可以通过贪心来求答案。

接下来考虑通过DP来维护答案。

记 $f_{i,j}$ 表示从第 $i$ 面墙考试，第 $j$ 个公司开始，最多能向后刷多少面墙。

所以 $f_{i,j}=\begin{cases}0&c_i\notin S_j\\f_{i+1,j+1}+1&c_i\in S_j\end{cases}$吗，其中 $S_j$ 表示第 $j$ 个公司可以刷的公司集合。

同时注意到，每一种颜色的公司很少，所以可以考虑每一次DP是更新所有的可以刷当前位置的公司即可，时间复杂度 $O(\sum f(c))$。

[APIO2020] 交换城市

题意：给定一张有边权的无向图，有两个人分别在不同的两个点，求在所有让两个人交换位置且不相遇的方案中，经过所有边的边权最大值的最小值是多少。

通过手玩或者证明，不难得到，两个点之间不能够相互到达，当且仅当他们两个点所在的连通块是一条链。

而我们维护的东西很像最小生成树，所以考虑类似的从小到大加入边，同时建出 Kruskal 重构树。

如果一条边破坏了某条链，就将它向链上所有的点连边；同时，他如果连接了两个非链连通块（包括连接了之后不是链的），它也会将这两个连通块连接在一起。

使用启发式合并维护加边过程，树剖实现重构树上求答案即可。

时间复杂度 $O(m\log m+n+Q\log n)$。

[APIO2020] 有趣的旅途

题意：给定一个每个点度数 $\leqslant 3$ 的树，给出一个树的排列 $a_0,a_1\dots a_{N-1}$，使得 $dis(a_0,a_1),dis(a_1,a_2)\dots dis(a_{N-2},a_{N-1})$ 不增。你只能通过 $4N$ 次询问获取树的信息，每一次可以得到两个点之间的距离，或者知道以某个点为根的时候，另一个点的子树的大小。

首先假设我们知道了树的形态，我们要如何构造答案。

一个很简单的想法就是我们会围绕着一个点打转，同时逐渐靠近这个点。

那么如果我们选择的这个点度数为 $2$ 就很好处理，我们记与它连接的两个连通块分别的 $T_1$ 和 $T_2$，则我们会交替选择 $T_1$ 和 $T_2$ 中距离我们选择的点最远的点。

但是，这样交替我们就必须要保证 $||T_1|-|T_2||\leqslant 1$，也就是两棵树的大小差不能超过 $1$，不难发现我们要选择的点就得是重心。

这样，我们就可以把这种构造方法推广到度数为 $3$ 的情况了，细节较多，可能要多调一会。

现在我再回头来考虑如何找到重心。

由于重心满足每一个子树的大小 $\leqslant \left\lfloor\dfrac{N}{2}\right\rfloor$，所以我们对于每一个点询问以 $0$ 号点为根，它的子树大小，只有这个值 $\geqslant \left\lceil\dfrac{N}{2}\right\rceil$ 才可能满足条件，发现买组条件的数构成一条链，其中重心应是链底，也就是询问出来的这个值最小的点。就此，我们花费了 $N$ 次询问得到了重心。

我们在花 $N$ 次询问询问每个点到重心的距离，直接得到重心的 $2\sim3$ 个儿子，然后询问每个点和其中 $1\sim 2$ 个孩子的距离，就可以得到每一个点所在的子树了。

接下来直接实现上述过程即可。

[APIO2021] 六边形领域

[APIO2021] 雨林跳跃

题意：给定一个 $n$ 个排列 $H$，每一个位置的点分别可以一步走到左端和右端离他最近且比他大的位置，问从 $[A,B]$ 中的某一个位置开始，至少要花多少步才能走到 $[C,D]$ 中的某一个，或判断无解。保证 $B<C$。

我们很容易用倍增 $O(\log n)$ 得到从一个点开始，走到一个区间的最少步数。

我们考虑贪心，首先，最优的路径不可能在过程中回到 $[A,B]$，所以最优解，同时尽可能高且保证能够到达的点一定更优。所以起点必然是从 $[A,B]$ 中能从 $B$ 出发到达且高度小于 $[C,D]$ 中最高点的点中高度最高的。

然后这个点的路径必然是向上跳（即向左右两边中更高的跳）一段，然后向右跳一段。

使用倍增实现，时间复杂度 $O((n+Q)\log n)$。

[APIO2021] 封闭道路

题意：给定一个有 $n$ 个节点的树，边有边权，对于 $k=0,1 \dots n-1$，求最小的边权和使得删去这些边之后，每一个点的度数 $\leqslant k$。

首先，考虑对于特定的 $k$ 进行DP，维护 $f_{u,0/1}$ 表示在 $u$ 节点的子树内，删/不删连向 $u$ 的父亲。然后使用堆根据 $f_{v,1}-f_{v,0}$ 的值从小到大排序来维护转移，这样可以做到单次 $O(n\log n)$，总体复杂度 $O(n^2\log n)$。

我们考虑降低复杂度。对于一个度数为 $d$ 的点，对于所有 $k\geqslant d$，它都不需要删点，也就意味着对应的DP值就是 $0$ 和到父亲的链的长度。

所以，我们考虑求解 $k$ 的时候只遍历度数 $\geqslant k$ 的点，而对于所有度数 $<k$ 的点，只需要提前将它的转移处理到与它相邻点的堆中即可。

使用可删除堆维护，复杂度为 $O(\sum d\log n)$ 即 $O(n\log n)$。

[APIO2022] 火星

[APIO2022] 游戏

题意：给定一张有向图，初始时有一条 $0$ 到 $k-1$ 的链，依次加入 $Q$ 条边，在线回答是否存在包含 $0$ 到 $k-1$ 中的至少一个节点的环。

来自水军的神秘做法。

由于初始时有从 $0$ 到 $k-1$ 的路径，所以可以对于每一个点 $u$，维护可以到达它的编号最大关键点 $s_u$ 和它可以到达的编号最小关键点 $t_u$。于是每一个点的对应一个区间 $[s_u,t_u]$，如果出现 $s_u>t_u$，就说明出现了环。

但是维护 $[s_u,t_u]$ 并不方便吗，所以考虑建出 $[-1,k]$ 的线段树，用线段树上包含这个区间的极小区间来代表他，这样，就可以通过每一个点的边界判断来查看这条边是否需要下传，但每一个点至多被下传 $O(\log k)$ 次，所以总体复杂度是 $O((n+m)\log k)$ 的。

[APIO2022] 排列

题意：构造一个排列，是的其递增子序列数为给定的 $k$。

考虑一个长为 $n$ 的单调上升，它对答案贡献的逆序对数为 $2^n$ 对，具体实现如下图。

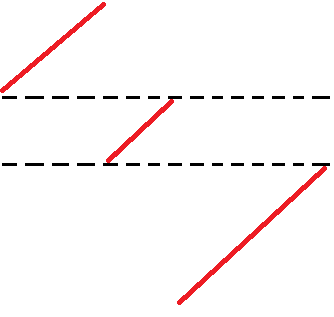
这样对于 $k$ 进行二进制拆分，可以做到 $B\log_2^2k$ 的序列长度，其中 $B>1$ 无法通过。

发现我们有很多的点都在做同一件事情：使得递增子序列数 $\times 2$。我们可以考虑维护一个长为 $\log_2k$ 的乘法部件，在需要的二进制位下挂一个数，表示加上对应的 $2^n$。实现如下图。

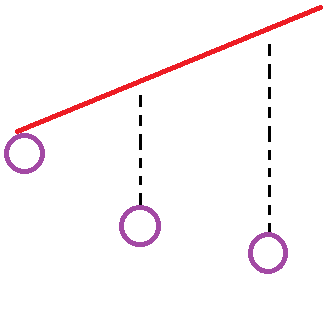
这样序列最长为 $2\log_2k$ 的，可以拿到比较优秀的部分分。

考虑继续优化。

如果同时出现 $2^n$ 和 $2^{n+1}$，我们可以将其改为 $3\times 2^n$。具体实现如下图。

如果蓝色和橙色的点分别对应 $2^{n+1}$ 和 $2^n$ 的点，我们在 $2^n$ 处挂一个红色点在左边两个紫色点上即可。这样子的序列长度最劣是 $1.5\log_2k+1$ 的，可以通过此题。